Intermediate Representations Chapter 4 Outline Issues in IR

Intermediate Representations (Chapter 4)

Outline • • • Issues in IR design High-Level IRs Medium-Level IRs Low-Level IRs Multi-Level IRs MIR, HIR, and LIR ICAN Representations Other IRs Conclusions (Informal Compiler Algorithm Notation)

Issues in IR Design • Portability • Optimization level • Complexity of the compiler – Reuse of legacy compiler parts – Compilation cost – Multi vs. One IR levels – Compiler maintenance

Example MIPS Compiler UCODE Stack Based IR Load/Store Based Architecture

Example MIPS Compiler UCODE Stack Based IR Translator Medium Level IR Optimizer Medium Level IR Translator UCODE Stack Based IR Code generator Load/Store Based Architecture

Example PA-RISC (HP-RISC) UCODE Stack Based IR Load/Store Based Architecture

Example PA-RISC (HP-RISC) UCODE Stack Based IR Translator Very low IR (SLLIC) Optimizer Very low IR (SLLIC) Code generator Load/Store Based Architecture

Why do we need multiple representations? • Lower representations expose more computations – more effective “standard” optimizations – examples: strength reduction, loop invariats, . . . • Higher representations provide more “nondeterminism” – more effective parallelization (reordering) – data cache optimizations

Example Arrays C-code float a[20][10]; . . . a[i][j+2] MIR t 1 j+2 r 1 [fp-4] t 2 i*20 r 2 r 1+2 t 3 t 1+t 2 r 3 [fp-8] t 4 4*t 3 t 4 r 3*20 addr(a) +4 (i*20 + j +2) t 5 addr a t 6 t 5+t 4 HIR t a[i, j+2] LIR t 7 *t 6 r 5 r 2+r 4 r 6 4*r 5 r 7 fp-216 f 7 [r 7+r 6]

External Representation • Internal IR representation is used in the compiler • External representation is needed for: – Compiler debugging – Cross-module integration • Design issues – Representing pointers – Unique representation of temporaries – Compaction

Outline • • • Issues in IR design High-Level IRs Medium-Level IRs Low-Level IRs Multi-Level IRs MIR, HIR, and LIR ICAN Representations Other IRs Conclusions

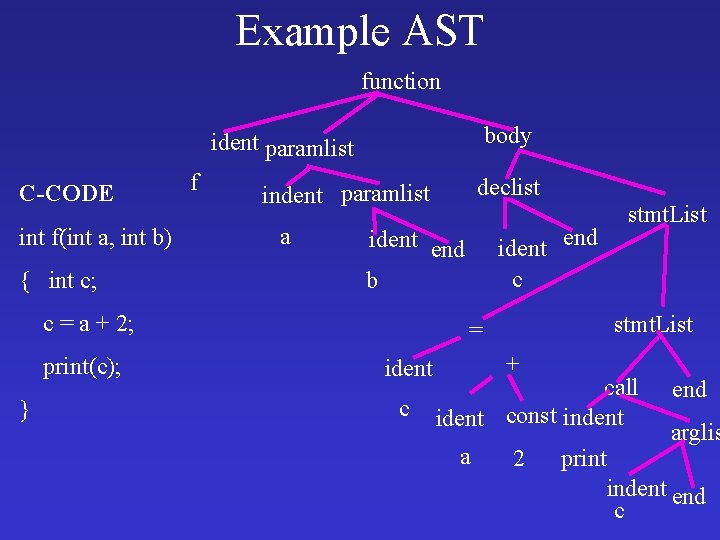
Abstract Syntax Trees • • Compact source representation No punctuation symbols Tree defines hierarchy Used for Front-Ends Sometimes include symbol table pointers Can be translated into HIR Can be also used for compaction

Example AST function body ident paramlist C-CODE int f(int a, int b) { int c; f a } ident end c ident end b c = a + 2; print(c); declist indent paramlist stmt. List = ident c stmt. List + call ident const indent a 2 print end arglis indent end c

Other HIRs • Normal linear forms: – Preserve control flow structures and arrays – Simplified control flow structures – Eliminate GOTOs – Continuations

Outline • • • Issues in IR design High-Level IRs Medium-Level IRs Low-Level IRs Multi-Level IRs MIR, HIR, and LIR ICAN Representations Other IRs Conclusions

Medium Level IR • Source and target language independent • Machine independent representation for program variables and temporaries • Simplified control flow constructs • Portable • Sufficient in many optimizing compilers: MIR, Sun-IR

Outline • • • Issues in IR design High-Level IRs Medium-Level IRs Low-Level IRs Multi-Level IRs MIR, HIR, and LIR ICAN Representations Other IRs Conclusions

Low Level IR • One to one correspondence with machine • Deviations from the machine – Alternative code – Addressing modes – Side effects? – Instruction selection in the last phase • Appropriate compiler data structure can hide dependence

Side Effect Operations (PA-RISC) PA-RISC (Option 1) LDWM 4(0, r 2), r 3 MIR L 1: t 2 *t 1 t 1+4 . . . ADDI 1, r 4 t 3+1 COMB, < r 4, r 5, L 1 t 5 t 3 < t 4 if t 5 goto L 1

Outline • • • Issues in IR design High-Level IRs Medium-Level IRs Low-Level IRs Multi-Level IRs MIR, HIR, and LIR ICAN Representations Other IRs Conclusions

Multi-Level Intermediate Representations • Multiple representations in the same language • Compromise computation exposure and high level description • SUN-IR: Arrays can be represented with multiple subscripts

Outline • • • Issues in IR design High-Level IRs Medium-Level IRs Low-Level IRs Multi-Level IRs MIR, HIR, and LIR ICAN Representations Other IRs Conclusions

Example C-code void make_node(p, n) struct node *p; int n; {struct node *q; q = malloc(sizeof(struct node)); q->next = nil; q->value=n; p->next = q; MIR make_node: begin receive p(val) receive n(val) q call malloc, (8, int) *q. next nil *q. value n *p. next q return } end

insert_node: C-code begin receive n(val); receive l(val) void insert_node( n, l) int n; struct node *l; {if (n > l. value) } t 1 * l. value; if n <= t 1 goto L 1 t 2 *l. next; if t 2 != nil goto L 2 call make_node, (l, type 1; n, int) return L 2: t 4 *l. next if (l->next == nil) make_node(l, n); call insert_node, (n, int, t 4, type 1) else insert_node(n, l->next); return L 1: return end

MIR Issues • MIN does not usually exist MIR t 1 t 2 min t 3 PA-RISC MOVE r 2, r 1 COM, >= r 3, r 2 MOVE r 3, r 1 • Both value and “location” computation for Boolean conditions t 3 t 1<t 2 if t 3 goto L 1 if t 1 < t 2 goto L 1

HIR • Obtained from MIR • Extra constructs – Array references – High level constructs

MIR v opd 1 t 2 opd 2 HIR t 3 opd 3 if t 2 > 0 goto L 2 for v opd 1 by opd 2 to opd 3 L 1: if v < t 3 goto L 3 instructions endfor instructions; v v + t 2 goto L 1 L 2: if v > t 3 goto L 3 instructions; goto L 2 L 3: v v + t 2

insert_node: begin C-code receive n(val); receive l(val) t 1 * l. value void insert_node( n, l) if n > t 1 then int n; t 2 *l. next; struct node *l; if t 2 = nil then {if (n > l. value) call make_node, (l, type 1; n, int) if (l->next == nil) make_node(l, n); return else insert_node(n, l->next); } else t 4 *l. next call insert_node, (n, int, t 4, type 1) return; fi; end

LIR • Obtained from MIR • Extra features: – Low level addressing – Load/Store • Eliminated constructs – Variables – Selectors – Parameters

insert_node: begin C-code s 800 s 1; s 801 s 2 s 802 [s 801+0]; if s 800<=s 802 goto L 1 void insert_node( n, l) s 803 [s 801+4]; if s 803!=nil goto L 2 int n; s 1 s 801; s 2 s 800 struct node *l; call make_node, ra {if (n > l. value) return if (l->next == nil) L 2: s 1 s 800; s 2 [s 801+4] call insert_node, ra make_node(l, n); return else insert_node(n, l->next); } L 1: return end

Outline • • • Issues in IR design High-Level IRs Medium-Level IRs Low-Level IRs Multi-Level IRs MIR, HIR, and LIR ICAN Representations Other IRs Conclusions

Representing MIR in ICAN • An MIR program can be (internally) represented as an abstract syntax tree • The general construction – A (union) type for every non-terminal – An enumerated type “kind” for every production – A tuple for every production • Other ideas – Flatten the hierarchy in some cases – Use functions to abstract MIR properties (simplifies semantic manipulations)

ICAN Tuples for MIR Instruction (Table 4. 7) Label: <kind: label, lbl: Label> receive Var. Name(Param. Type) <kind: receive, left: Var. Name, ptype: Param. Type> Var. Name Operand 1 Binop Operand 2 <kind: binasgn, left: var. Name, opr: Binop, opd 1: Operand 1, opd 2: Operand 2> Var. Name Unop Operand <kind: unasgn, left: Var. Name, opr: Unop, opd: Operand> Var. Name Operand <kind: valasgn, left: Var. Name, opd: Operand> . . .

IRoper = enum{ add, || + sub, || - (unary) mul, || * (binary) div, || / mod, min, max, eql, neql, less, lseq, grtr, gteq, || =, !=, <, <=, >, >= shl, shra, and, or, xor ind, || * pointer-dereference indelt, || *. dereference to a field neg, || - (unary) not, || ! addr, val, cast || (type cast) Table 4. 6

MIRkind = enum {label, receive, binasgn, unasgn, . . . , sequence} Opkind = enum { var, const, type} Exp. Kind = enum { binexp, unexp, noexp, listexp} Exp_Kind : Mir. Kind Exp. Kind Has_Left: Mir. Kind boolean Exp_Kind : = {<label, noexp>, <receive, noexp>, <binassgn, binexp> <unasgn, unexp>, . . . <callexp, listexp>, . . . <sequence, noexp>} Has_Left : = {<label, false>, <receive, true>, <binasgn, true>, <unasgn, true>, <valasgn, true>, <condasgn, true> <castasgn, true>, . . , <unif, false>, . . . }

Inst: array[1. . n] of Instructions Inst[1] =<kind: label, lbl: ”L 1”> Inst[2]=<kind: valasgn, left: ”b”, MIR L 1: b a c b+1 opd: <kind: var, val: ”a”>> Inst[3]=<kind: binasgn, left: “c”, opr: add, opd 1: <kind: var, val: “b”>, opd 2: <kind: const, val: “ 1”>>

insert_node: begin receive n(val); receive l(val) t 1 * l. value; if n <= t 1 goto L 1 t 2 *l. next; if t 2 != nil goto L 2 call make_node, (l, type 1; n, int) return L 2: t 4 *l. next call insert_node, (n, int, t 4, type 1) return L 1: return end Fig 4. 9

Representing HIR in ICAN • Similar to MIR (Table 4. 8) • For statement has three expressions (Figure 4. 10) • Break “if” and “for”

Representing LIR in ICAN • Similar to MIR (Table 4. 9, 4. 10) • No list expressions (Figure 4. 11)

Example (4. 12, 4. 13) Inst[1] =<kind: label, lbl: “L 1”> L 1: r 1 [r 7+4] r 2 [r 7+8] Inst[2] =<kind: loadmem, left: “r 1”, addr: <kind: addrrc, r 3 r 1 + r 2 reg: “r 7”, r 4 -r 3 disp: 4, len: 4>> if r 3 > 0 goto L 2 r 5 (r 9) r 1 [r 7 -8](2) r 5 L 2: return r 4 Inst[3] =<kind: loadmem, left: “r 2”, addr: <kind: addr 2 r, reg: “r 7”, reg 2: “r 8”, len: 4>>

HIR, MIR, LIR as an ADT • View IR as an abstract data type • Example fields: – Proc. Name - the procedure name – Nblocks - the number of basic blocks – ninsts: array[1. . nblocks] of integer – Block: array[1. . nblocks] of array [. . ] of Instruction – Succ, Pred: Integer set of integer • Example methods – insert_before(i, j, ninsts, Block, inst)

Outline • • • Issues in IR design High-Level IRs Medium-Level IRs Low-Level IRs Multi-Level IRs MIR, HIR, and LIR ICAN Representations Other IRs Conclusions

Triples • Three address instructions • Implicit names for results (instruction index) • No need for temporary names • Usually represented via pointers – Program transformations may be tricky • Can be translated from/into MIR

MIR L 1: i i+ 1 TRIPLES (1) i+ 1 (2) i sto (1) t 1 i +1 (3) i +1 t 2 p+4 (4) p+4 t 3 *t 2 (5) (*4) p t 2 (6) p sto (4) t 4 t 1 <10 (7) (3) <10 *r t 3 (8) r *sto (5) if t 4 goto L 1 if (7), (1)

Trees • Compact representation for expressions • A basic block is a sequence of trees • Assignments can be implicit or explicit i i: add i i 1 1

MIR L 1: i i+ 1 t 1 i +1 t 2 p+4 t 3 *t 2 p t 2 t 4 t 1 <10 *r t 3 if t 4 goto L 1 Trees

Combining trees may lead to incorrect computation b: add a a+1 a: add b a+a a 1

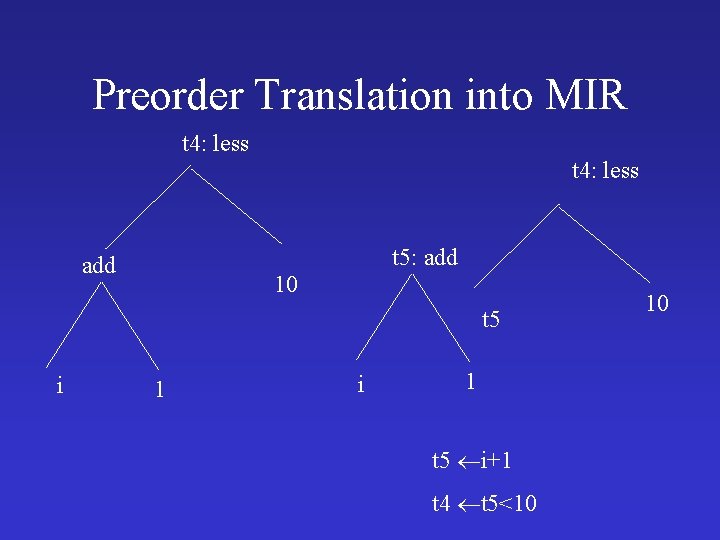
Preorder Translation into MIR t 4: less t 5: add 10 t 5 i 1 t 5 i+1 t 4 t 5<10 10

Advantages of Trees • Minimize temporaries • Amenable to many optimizations • Locally optimized code with register allocation can be used • Easy to translate into Polish-Prefix code (used for automatic instruction selection)

Directed Acyclic Graphs (DAGs) • A combination of trees • Operands which are reused are linked • Nodes may be annotated with variable names

MIR L 1: i i+ 1 t 1 i +1 t 2 p+4 t 3 *t 2 p t 2 t 4 t 1 <10 *r t 3 if t 4 goto L 1 DAG

MIR c a b a +1 c 2*a d -c c a+1 c b +a d 2 *a b c DAG

Properties of DAGs • Very compact • Local common sub-expression elimination • Not so easy to optimize

Conclusions • Representations in the book – HIR, MIR, LIR • Other representations – Triples, Trees, DAGs, Stack machines – Source language dependent • Algol Object Code(1960) • Pascal P-code (1980) • Prolog Warren machine code (1977) • Java bytecode (1996) – Microsoft. net?