Intermediate Code Representations Conceptual phases of compiler Lexical

Conceptual phases of compiler Lexical Analysis (scanner) Syntax analysis (parser) Semantic Analysis Code optimization

IR – Encodes Compiler’s Program Knowledge Thus, some IR PROPERTIES: • • • Ease

3 Categories of IRs 1. Structural/Graphical - AST and Concrete ST - call graph

Level of Abstraction Consider: A[j, i] = @A + j*10 + i [] A

Some Design Issues for IRs Questions to Ponder: 1. What is the minimum needed

High Level Graphical Representations Consider: A -> V : = E E -> E

Linear IRs: Three Address Code • Sequence of instructions of the form X :

Simple Linear IRs Write the 3 – address code for: a : = b

Exercise • Give the 3 address code for: • Z : = x *

More Simple Linear IRs Stack machine code: push, pop, ops Consider: x – 2

Call Graph Representation Node = function or method Edge from A to B :

Slides: 22

Download presentation

Intermediate Code Representations

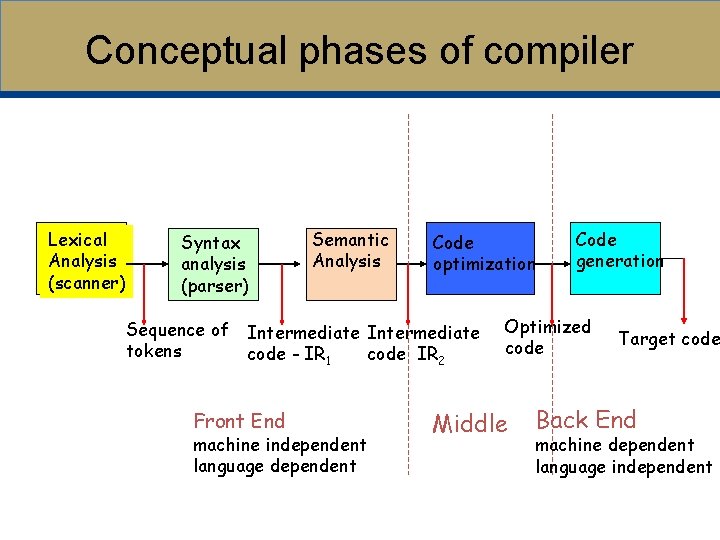
Conceptual phases of compiler Lexical Analysis (scanner) Syntax analysis (parser) Semantic Analysis Code optimization Sequence of Intermediate tokens code - IR 1 code IR 2 Front End machine independent language dependent Code generation Optimized code Middle Target code Back End machine dependent language independent

Why use an IR?

IR – Encodes Compiler’s Program Knowledge Thus, some IR PROPERTIES: • • • Ease of generation Ease of manipulation Size Freedom of Expression Level of Abstraction Selecting IR is critical.

3 Categories of IRs 1. Structural/Graphical - AST and Concrete ST - call graph - program dependence graph (PDG) 2. Linear - 3 -address code - abstract stack machine code 3. Hybrid - control flow graph (CFG)

Level of Abstraction Consider: A[j, i] = @A + j*10 + i [] A I J Loadi 1, R 1 Sub RJ, R 1, R 2 Loadi 10, R 3 Mult R 2, R 3, R 4 Sub Ri, R 1, r 5 Add R 4, R 5, R 6 Loadi @A, R 7 Add R 7, R 6, R 8 Load R 8, RAIJ

Some Design Issues for IRs Questions to Ponder: 1. What is the minimum needed in the language’s set of operators? 2. What is the advantage of a small set of operators? 2. What is the concern of designing the operations Close to actual machine operations? 4. What is the potential problem of having a small Set of IR operations?

High Level Graphical Representations Consider: A -> V : = E E -> E + E | E * E | - E | id String: a : = b * - c + b * - c Exercise: Concrete ST? AST? DAG?

Linear IRs: Three Address Code • Sequence of instructions of the form X : = y op z where x, y and z are variable names, constants, or compiler generated variables (“temporaries”) • Only one operator is permitted on the RHS – expressions computed using temporaries 9

Simple Linear IRs Write the 3 – address code for: a : = b * - c + b * - c ? = -c =b*? … complete the code from the ast? The dag?

Exercise • Give the 3 address code for: • Z : = x * y + a[j] / sum(b) 14

More Simple Linear IRs Stack machine code: push, pop, ops Consider: x – 2 * y Advantages?

Hybrid IRs

Exercise – Construct the CFG

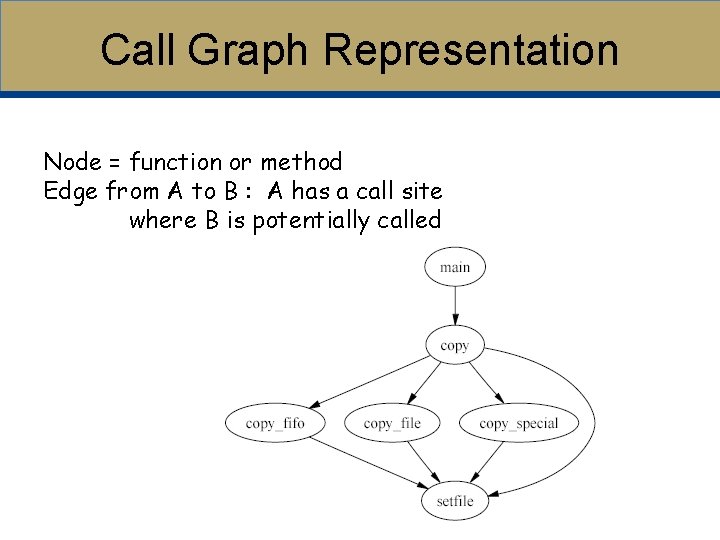
Call Graph Representation Node = function or method Edge from A to B : A has a call site where B is potentially called

Exercise: Construct a call graph

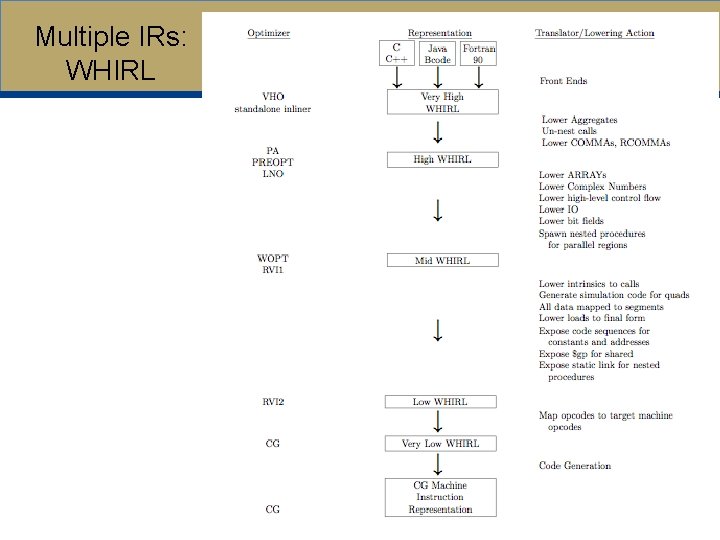
Multiple IRs: WHIRL

Key Highlights of IRs