Intermediate Algebra Chapter 4 Systems of Linear Equations

Intermediate Algebra Chapter 4 • Systems • of • Linear Equations

Objective • Determine if an ordered pair is a solution for a system of equations.

System of Equations • Two or more equations considered simultaneously form a system of equations.

Checking a solution to a system of equations • 1. Replace each variable in each equation with its corresponding value. • 2. Verify that each equation is true.

Graphing Procedure • 1. Graph both equations in the same coordinate system. • 2. Determine the point of intersection of the two graphs. • 3. This point represents the estimated solution of the system of equations.

Graphing observations • Solution is an estimate • Lines appearing parallel have to be checked algebraically. • Lines appearing to be the same have to be checked algebraically.

Classifying Systems • Meet in Point – Consistent – independent • Parallel – Inconsistent – Independent • Same – Consistent - Dependent

Def: Dependent Equations • Equations with identical graphs

Independent Equations • Equations with different graphs.
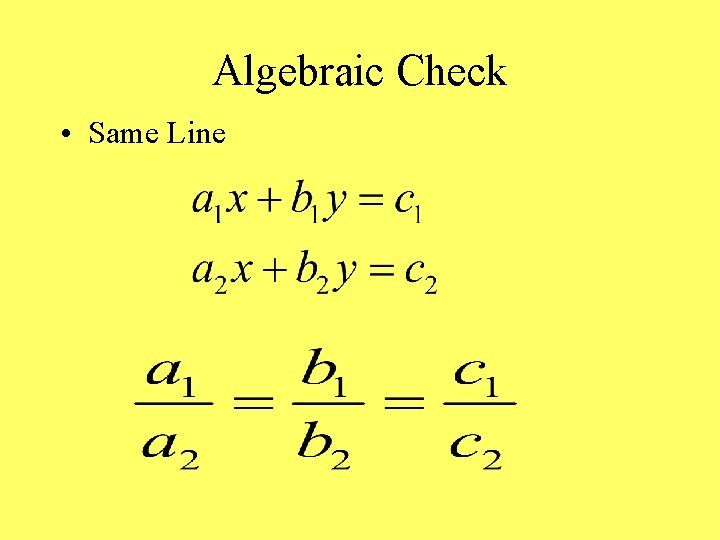
Algebraic Check • Same Line

Algebraic Check • Parallel Lines

Algebraic Check • Meet in a point {(x, y)}

Calculator Method for Systems • Solve each equation for y • Input each equation into Y= • Graph • Set Window • Use Cal Intersect

Calculator Problem

Calculator Problem 2

Calculator Problem 3

Objective • Solve a System of Equations using the Substitution Method.

Substitution Method • 1. Solve one equation for one variable • 2. In other equation, substitute the expression found in step 1 for that variable. • 3. Solve this new equation (1 variable) • 4. Substitute solution in either original equation • 5. Check solution in original equation.

Althea Gibson – tennis player • “No matter what accomplishments you make, someone helped you. ”

Intermediate Algebra • The • Elimination • Method

Notes on elimination method • Sometimes called addition method • Goal is to eliminate on of the variables in a system of equations by adding the two equations, with the result being a linear equation in one variable.

Write both equations in ax + by = c form • 2. If necessary, multiply one or both of the equations by appropriate numbers so that the coefficients of one of the variables are opposites. • 1.

Procedure for addition method cont. • 3. Add the equations to eliminate a variable. • 4. Solve the resulting equation • 5. Substitute that value in either of the original equations and solve for the other variable. • 6. Check the solution.

Procedure for addition method cont. • Solution could be ordered pair. • If a false statement results i. e. 1 = 0, then lines are parallel and solution set is empty set. (inconsistent) • If a true statement results i. e. 0 = 0, then lines are same and solution set is the line itself. (dependent)

Practice Problem • Answer {(2, 4)}

Practice Problem Hint: eliminate x first • Answer {(-7/2, -4)}

Practice Problem

Practice problem

Special Note on Addition Method • Having solved for one variable, one can eliminate the other variable rather than substitute. • Useful with fractions as answers.

Practice Problem – eliminate one variable and than the other • Answer: {(8/3, 1/3)}

Confucius • “It is better to light one small candle than to curse the darkness. ”

Intermediate Algebra 4. 2 • Systems • Of • Equations • In • Three Variables

Objective • To use algebraic methods to solve linear equations in three variables.

Def: linear equation in 3 variables • is any equation that can be written in the standard form ax + by +cz =d where a, b, c, d are real numbers and a, b, c are not all zero.

Def: Solution of linear equation in three variables • is an ordered triple (x, y, z) of numbers that satisfies the equation.

Procedure for 3 equations, 3 unknowns • 1. Write each equation in the form ax +by +cz=d • Check each equation is written correctly. • Write so each term is in line with a corresponding term • Number each equation

Procedure continued: • 2. Eliminate one variable from one pair of equations using the elimination method. • 3. Eliminate the same variable from another pair of equations. • Number these equations

Procedure continued • 4. Use the two new equations to eliminate a variable and solve the system. • 5. Obtain third variable by back substitution in one of original equations

Procedure continued • Check the ordered triple in all three of the original equations.

Sample problem 3 equations

Answer to 3 eqs-3 unknowns • {(-2, 3, 1)}

Bertrand Russell – mathematician (1872 -1970) • “Mathematics takes us still further from what is human, into the region of absolute necessity, to which not only the actual world, but every possible world, must conform. ”

Cramer’s Rule • Objective: Evaluate determinants of 2 x 2 matrices • Objective: Solve systems of equations using Cramer’s Rule

Determinant

Cramer’s rule intuitive • Each denominator, D is the determinant of a matrix containing only the coefficients in the system. To find D with respect to x, we replace the column of s-coefficients in the coefficient matrix with the constants form the system. To find D with respect to y, replace the column of ycoefficients in the coefficient matrix sit the constant terms.

Sample Problem: Evaluate: • Answer = 16

Sample Cramer’s Rule problem • Solve by Cramer’s Rule
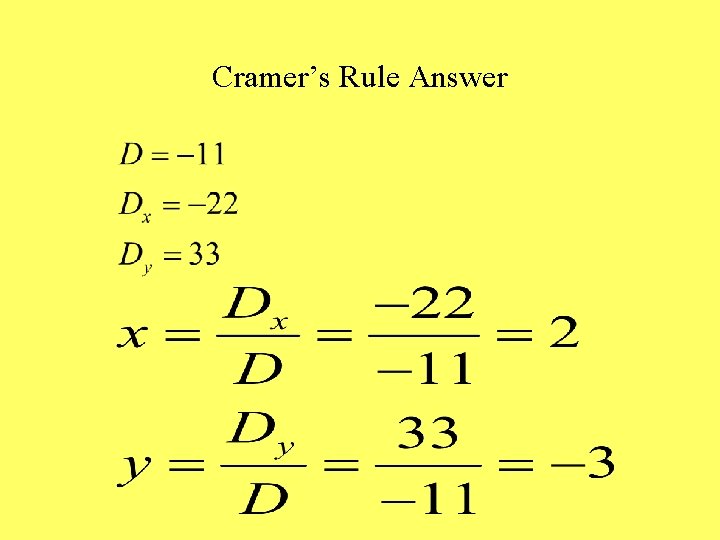
Cramer’s Rule Answer

Senecca • “It is not because things are difficult that we do not dare, it is because we do not dare that they are difficult. ”

Intermediate Algebra 5. 5 • Applications • Objective: Solve application problems using 2 x 2 and 3 x 3 systems.

Mixture Problems • ****Use table or chart • Include all units • Look back to test reasonableness of answer.

Sample Problem • How many milliliters of a 10% HCl solution and 30% HCl solution must be mixed together to make 200 milliliters of 15% HCl solution?

Mixture problem equations

Mixture problem answers • 150 mill of 10% sol • 50 mill of 30% sol • Gives 200 mill of 15% sol

Distance Problems • Include Chart and/or picture • Note distance, rate, and time in chart • D = RT and T = D/R and R=D/T • Include units • Check reasonableness of answer.

Sample Problem • To gain strength, a rowing crew practices in a stream with a fairly quick current. When rowing against the stream, the team takes 15 minutes to row 1 mile, whereas with the stream, they row the same mile in 6 minutes. Find the team’s speed in miles per hour in still water and how much the current changes its speed.

Distance problem equations

Answer • Team row 7 miles per hour in still water • Current changes speed by 3 miles per hour


Joe Paterno – college football coach • “The will to win is important but the will to prepare is vital. ”
- Slides: 60