Interlude for trees l l Joyce Kilmer Balanced

Interlude for trees l l Joyce Kilmer Balanced Trees Ø Ø Splay Red-Black AVL B-tree CPS 100, Spring 2010 15. 1

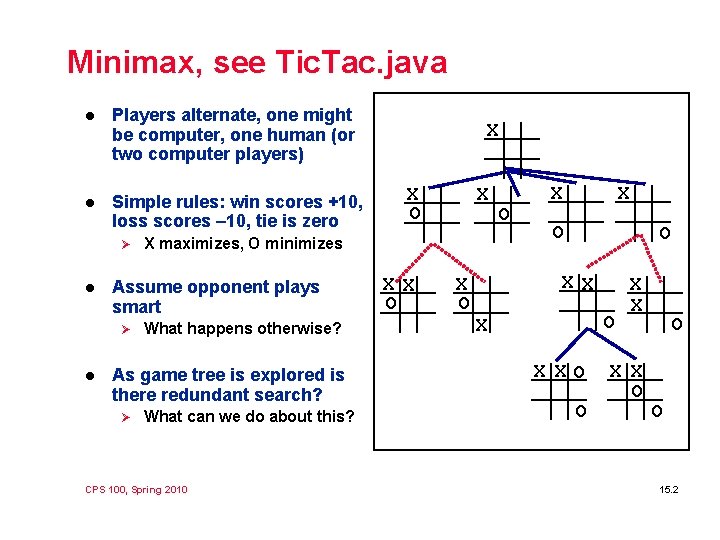
Minimax, see Tic. Tac. java l Players alternate, one might be computer, one human (or two computer players) l Simple rules: win scores +10, loss scores – 10, tie is zero Ø l l What happens otherwise? As game tree is explored is there redundant search? Ø X X O X maximizes, O minimizes Assume opponent plays smart Ø X What can we do about this? CPS 100, Spring 2010 XX O O X X XO O X X O O O 15. 2

Balanced Trees and Complexity l A tree is height-balanced if Ø Left and right subtrees are height-balanced Ø Left and right heights differ by at most one boolean is. Balanced(Tree root){ if (root == null) return true; return is. Balanced(root. left) && is. Balanced(root. right) && Math. abs(height(root. left) – height(root. right)) <= 1; } } CPS 100, Spring 2010 15. 3

Rotations and balanced trees l l Height-balanced trees Ø For every node, left and right subtree heights differ by at most 1 Ø After insertion/deletion need to rebalance Ø Every operation leaves tree in a balanced state: invariant property of tree Find deepest node that’s unbalanced then make sure: Ø On path from root to inserted/deleted node Ø Rebalance at this unbalanced point only CPS 100, Spring 2010 Are these trees height-balanced? 15. 4

What is complexity? l Assume trees are “balanced” in analyzing complexity Ø Ø l How to develop recurrence relation? Ø Ø l Roughly half the nodes in each subtree Leads to easier analysis What is T(n)? What other work is done? How to solve recurrence relation Ø Ø Plug, expand, plug, expand, find pattern A real proof requires induction to verify correctness CPS 100, Spring 2010 15. 5

Balanced trees we won't study l B-trees are used when data is both in memory and on disk Ø Ø l File systems, really large data sets Rebalancing guarantees good performance both asymptotically and in practice. Differences between cache, memory, disk are important Splay trees rebalance during insertion and during search, nodes accessed often more closer to root Other nodes can move further from root, consequences? • Performance for some nodes gets better, for others … Ø No guarantee running time for a single operation, but guaranteed good performance for a sequence of CPS 100, Spring 2010 operations, this is good amortized cost (Array. List. add)15. 6 Ø

Balanced trees we will study l l Both kinds have worst-case O(log n) time for tree operations AVL (Adel’son-Velskii and Landis), 1962 Ø Ø Ø l Nodes are “height-balanced”, subtree heights differ by 1 Rebalancing requires per-node bookkeeping of height http: //people. ksp. sk/~kuko/bak/ Red-black tree uses same rotations, but can rebalance in one pass, contrast to AVL tree Ø Ø Ø In AVL case, insert, calculate balance factors, rebalance In Red-black tree can rebalance on the way down, code is more complex, but doable Standard java. util. Tree. Map/Tree. Set use red-black CPS 100, Spring 2010 15. 7

Rotation do. Left (see AVLSet. java) l N N C A B C l Why is this called do. Left? Ø N will no longer be root, new value in left subtree Ø Left child becomes new root Unbalanced by two (not one!) Ø If left, left (or right, right) Node do. Left(Node root) • do. Left (do. Right) { Ø Otherwise need two • do. Left/do. Right Node new. Root = root. left; Ø First to get to left, left root. left = new. Root. right; • Or to right, right new. Root. right = root; return new. Root; } CPS 100, Spring 2010 15. 8

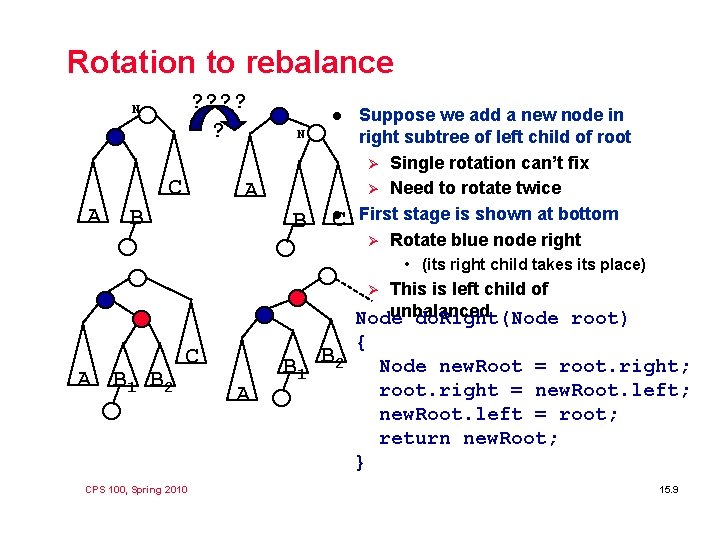
Rotation to rebalance ? ? ? N C A l N A B B C l Suppose we add a new node in right subtree of left child of root Ø Single rotation can’t fix Ø Need to rotate twice First stage is shown at bottom Ø Rotate blue node right • (its right child takes its place) This is left child of unbalanced Node do. Right(Node root) Ø A B 1 B 2 C A B 1 B 2 { Node new. Root = root. right; root. right = new. Root. left; new. Root. left = root; return new. Root; } CPS 100, Spring 2010 15. 9

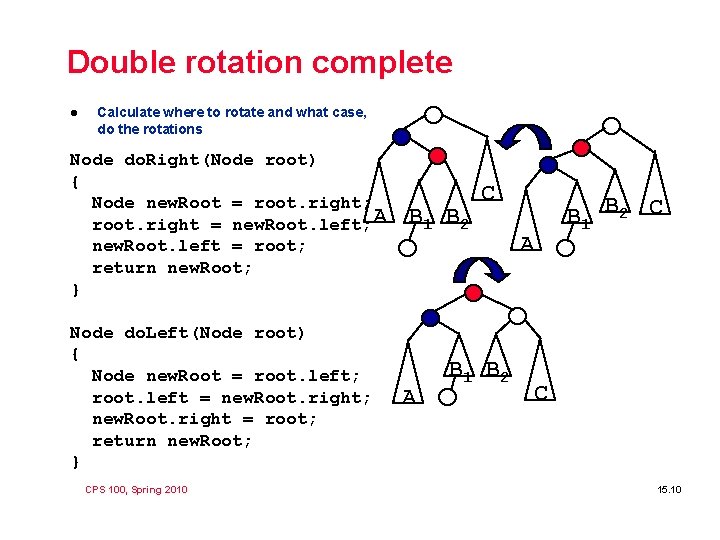
Double rotation complete l Calculate where to rotate and what case, do the rotations Node do. Right(Node root) { Node new. Root = root. right; root. right = new. Root. left; A new. Root. left = root; return new. Root; } Node do. Left(Node root) { Node new. Root = root. left; root. left = new. Root. right; new. Root. right = root; return new. Root; } CPS 100, Spring 2010 B 1 B 2 A C B 1 B 2 A B 1 B 2 C C 15. 10

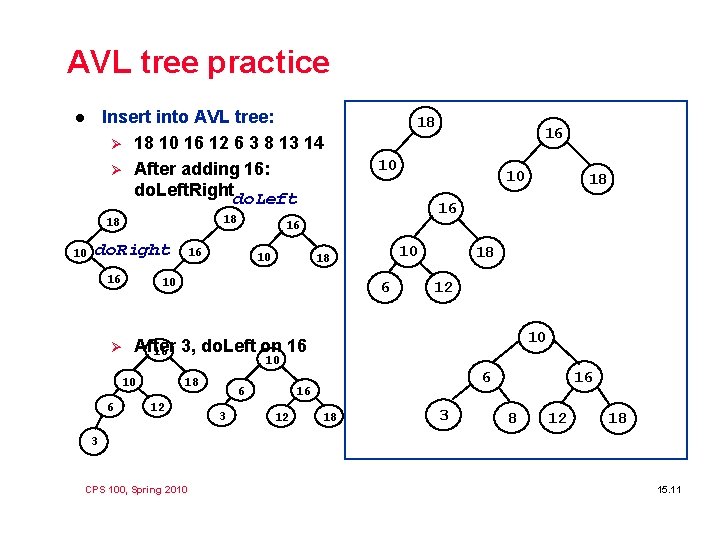
AVL tree practice Insert into AVL tree: Ø 18 10 16 12 6 3 8 13 14 Ø After adding 16: do. Left. Rightdo. Left l 18 18 10 do. Right 16 10 10 18 16 16 10 10 18 6 18 12 10 After 16 3, do. Left on 16 10 10 6 16 16 10 Ø 18 18 12 6 3 6 16 12 18 3 16 8 12 18 3 CPS 100, Spring 2010 15. 11

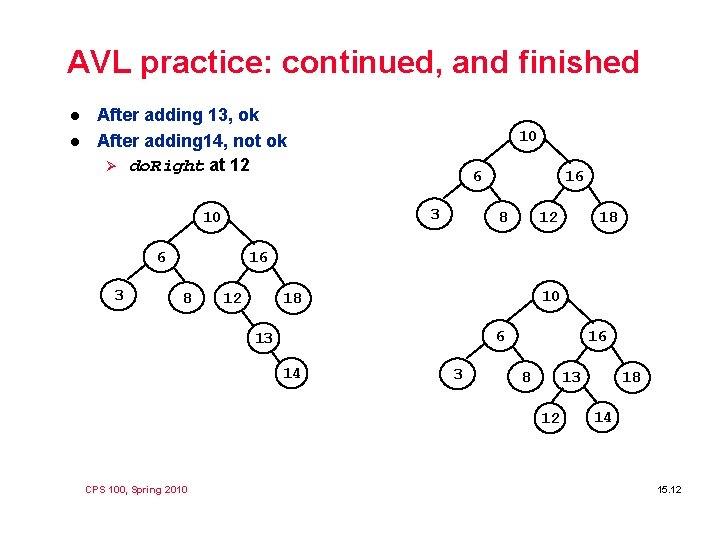
AVL practice: continued, and finished l l After adding 13, ok After adding 14, not ok Ø do. Right at 12 6 3 10 16 8 12 18 16 8 12 10 18 6 13 14 3 16 8 13 12 CPS 100, Spring 2010 18 14 15. 12

Lynn Conway See Wikipedia and lynnconway. com l Joined Xerox Parc in 1973 Ø Revolutionized VLSI design with Carver Mead Joined U. Michigan 1985 l Ø l Professor and Dean, retired '98 NAE '89, IEEE Pioneer '09 Helped invent dynamic scheduling early '60 s IBM l l Transgender, fired in '68 CPS 100, Spring 2010 15. 13