Interior Angle Measure Lesson and Questions Watch ME

Interior Angle Measure Lesson and Questions Watch ME As a SLIDESHOW

SKILL # 1 • Finding the SUM of the interior angles of any polygon. 360 degrees 180 degrees 1080 degrees 540 degrees • Our 1 st job will be to find the SUM of the interior angles for any shaped polygon!!

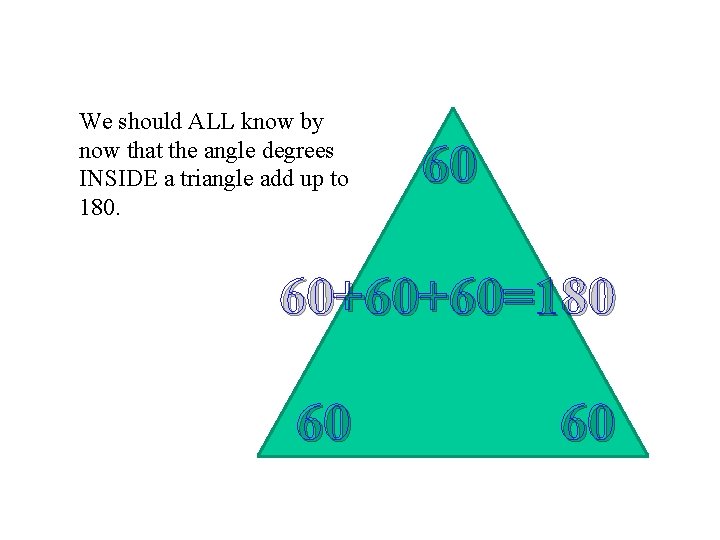
We should ALL know by now that the angle degrees INSIDE a triangle add up to 180. 60 60+60+60=180 60 60

• It doesn’t matter what shape your triangle is in!! The sum of the interior angles STILL measures 180. 30 120 30+30+120=180 30 • So what about other polygons, like a square or rectangle? ?

• Squares and rectangles have ALL 90 degree angles. So 4 x 90 = 360 degrees. 90 90 • Another way, since we KNOW that ALL triangles have 180 degrees, is to see how many triangles are in a figure, and then multiply the # of triangles by 180! • OR, # of triangles x 180 gives us the SUM of the interior angle measures for ANY polygon.

• So if you count how many triangles there are inside ANY polygon, and then multiply by 180 degrees, you will know the SUM of the interior angle measures. Let’s look at a rectangle. 180 degrees 2 180 degrees 1 First we divide our figure into triangles. Which gives us 2 triangles. • So 2 triangles x 180 = 360 degrees inside of a rectangle. We already knew this, BUT this proves that this method works.

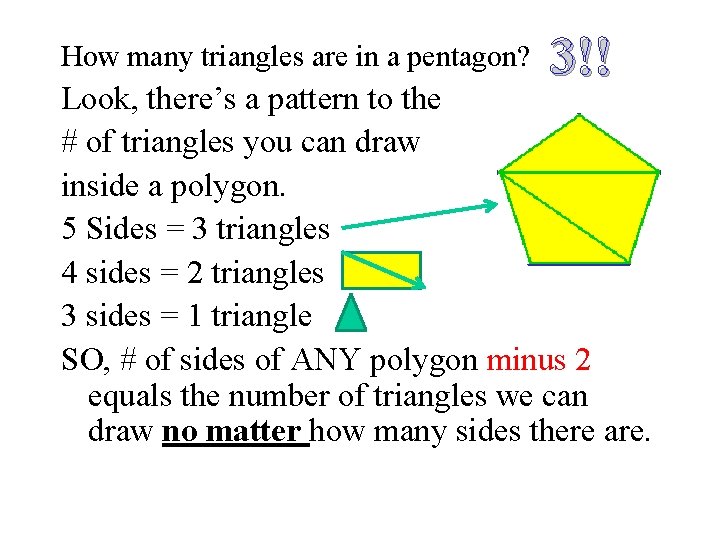
How many triangles are in a pentagon? 3!! Look, there’s a pattern to the # of triangles you can draw inside a polygon. 5 Sides = 3 triangles 4 sides = 2 triangles 3 sides = 1 triangle SO, # of sides of ANY polygon minus 2 equals the number of triangles we can draw no matter how many sides there are.

How many triangles can you draw in a decagon? That’s 10 -2 = 8 18 348 8 . a 20 -gon? That’s 20 -2 = 18 triangles A 350 -gon? That’s 350 -2 = 348 triangles Once we know how many triangles we can draw, IT’S EASY, just multiply by 180 degrees to find the SUM of the interior angles. S = Sum of angle measures The formula for this is S = ( n-2) *180 You either have to memorize this formula, OR just remember to subtract 2 from the # of sides and multiply by 180. n = # of sides of the polygon

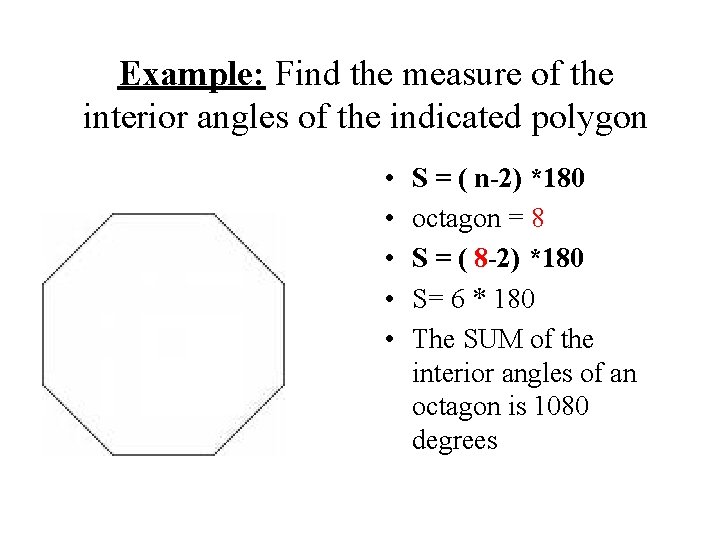
Example: Find the measure of the interior angles of the indicated polygon • • • S = ( n-2) *180 octagon = 8 S = ( 8 -2) *180 S= 6 * 180 The SUM of the interior angles of an octagon is 1080 degrees

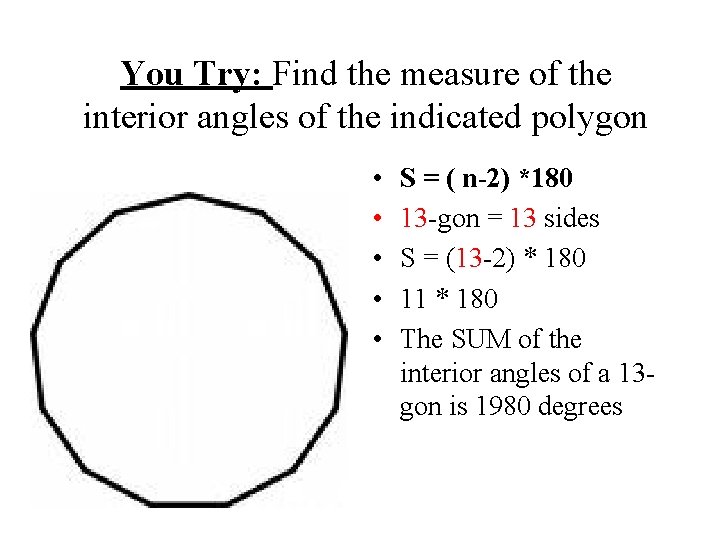
You Try: Find the measure of the interior angles of the indicated polygon • • • S = ( n-2) *180 13 -gon = 13 sides S = (13 -2) * 180 11 * 180 The SUM of the interior angles of a 13 gon is 1980 degrees

Practice. Do this problem before you click again to check answer. Find the measure of the interior angles of the indicated polygon A polygon has 14 sides. Find the sum of the interior angle measures of this polygon. Since we know the number of sides, we just need to subtract 2 and multiply by 180 degrees. 14 – 2 = 12 ( this is how many triangles we could draw inside this figure. ) 12 * 180 = 2160 degrees. If we use the equation to solve, we get S = ( 14 -2)180 = 2160 degrees.

SKILL # 2 • Find the # of sides of any regular polygon if we know the SUM of the angle measures inside. • We’ll use the same formula, S = ( n-2) *180 fill in for S, and solve for n.

What is a “REGULAR” polygon? ? Regular polygon: a polygon that has ALL the Same side lengths AND all the same Angle measures inside. ALL Same sides, same angles When we are dealing with a regular polygon , we can use the Sum of the angle measures to help us find the length of ONE side or ONE of the angle measures inside the figure. We will learn this in the next few slides. Example: We know a square( which is a “regular” polygon) has a total of 360 degrees of angle measures inside. We also know that each of those angles is 90 degrees and each side is the same length. This is a good example to help you understand that if you have a “regular” polygon, it will have ALL of the same side lengths and ALL of the angle measures inside.

• Example: The sum of the measures of the interior angles of a regular polygon is 1440 degrees. Classify the polygon by the number of sides. • S = ( n-2) *180 • They gave us that S = 1440, sub it in for S. • 1440 = ( n-2) *180 • Solve for n Divide by 180 • 1440/180 = n-2 1440/180 = 8 • 8 = n-2 , then add 2 to both sides and get n=10. • What’s a 10 sided figure, a decagon!!

You Try: The sum of the measures of the interior angles of a regular polygon is 3600 degrees. This regular polygon has how many sides? - S = ( n-2) *180 - They gave us that S = 3600, sub it in. 3600 = ( n-2) *180 Solve for n Divide by 180 3600/180 = n-2 = 20 and get n=22. 20 = n-2 , then add 23600/180 both sides What’s a 22 sided figure, a 22 -gon!!

Practice. Do this problem before you click again to check answer. QUESTION: The sum of the measures of the interior angles of a regular polygon is 3060 degrees. This regular polygon has how many sides? S = ( n-2) *180 They gave us that S = 3060, sub it in. 3060 = ( n-2) *180 Divide by 180 Solve for n 3060/180 = 17 3060/180 = n-2 17 = n-2 , then add 2 both sides and get n=19. What’s a 22 sided figure, a 19 -gon!!

SKILL # 3 • Find the angle measure of ONE angle inside any regular polygon if we know the SUM of the angle measures inside. • Step 1: Figure out # of sides. • Step 2: Divide Sum of interior angle measures by # of sides. Example: Let’s look at our square again. We know a square( which is a “regular” polygon) has a total of 360 degrees and 4 sides. So 360 degrees divided by 4 = 90 degrees. One angle measure inside a square is 90 degrees. And we know this is true. SEE, dividing total angle measure by # of sides WORKS!! Example: Let’s look at a triangle. We know a regular triangle has a total of 180 degrees and 3 sides. So 180 degrees divided by 3 = 60 degrees. One angle measure inside a regular triangle is 60 degrees. SEE!! It works.

• Example: The sum of the measures of the interior angles of a regular polygon is 1440 degrees. Find the measure of ONE of Step 1: Figure how the angles inside this figure. many sides this • S = ( n-2) *180 polygon has • They gave us that S = 1440, sub it in for S. • 1440 = ( n-2) *180 Divide by 180 • Solve for n 1440/180 = 8 • 1440/180 = n-2 • 8 = n-2 , then add 2 to both sides and get n=10. So 10 Sides Step 2: Divide the • 1440 divided by 10 = 144 degrees. Sum of the angle • So ONE interior angle of a decagon is 144 degrees. measures they gave us by the # of sides. • Because it’s regular, ALL angles inside are the same, 144 degrees Remember: This ONLY works with regular polygons.

• You Try: The sum of the measures of the interior angles of a regular polygon is 3600 degrees. Find the measure of ONE of Step 1: Figure how the angles inside this figure. many sides this • S = ( n-2) *180 polygon has • They gave us that S = 3600, sub it in for S. • 3600 = ( n-2) *180 Divide by 180 • Solve for n 3600/180 = 20 • 1440/180 = n-2 • 20 = n-2 , then add 2 to both sides and get n=22. So 22 Sides Step 2: Divide the • 3600 divided by 22 = 163. 6 degrees. Sum of the angle • So ONE interior angle of a 22 -agon is 163. 6 degrees. measures they gave us by the # of sides. • Because it’s regular, ALL angles inside are the same, 163. 6 degrees Remember: This ONLY works with regular polygons.

Practice. Do this problem before you click again to check answer. • QUESTION #3: The sum of the measures of the interior angles of a regular polygon is 540 degrees. Find the measure of ONE of the angles inside this figure. Step 1: Figure how many sides this polygon has S = ( n-2) *180 They gave us that S = 540, sub it in for S. 540 = ( n-2) *180 Divide by 180 Solve for n 540/180 = 3 1440/180 = n-2 3 = n-2 , then add 2 to both sides and get n=5. So 5 Sides Step 2: Divide the 540 divided by 5 = 108 degrees. Sum of the angle So ONE interior angle of a pentagon is 108 degrees. measures they gave Because it’s regular, ALL angles inside are the same, us by the # of sides. 108 degrees Remember: This ONLY works with regular polygons.

Now, practice your skills at the following websites. Practice Site #1 Practice Site #2 Still struggling. Check out the COOL MATH Lesson on interior angle measures. COOL Math Lesson NOW, If you feel like you’re ready, do the questions on the next slide.

Practice problems Directions. Write these problems down and SOLVE with work, put in your class IN BOX behind my desk. This is worth an offline completion grade. You may use your notes. 1. 2. 3. 4. 5. 6. What is the SUM of the interior angles of a regular 15 -gon? How many sides does a regular polygon have with an interior angle sum of 5940 degrees? Classify a polygon by it’s sides if its interior angle measure is 1260 degrees. What is the SUM of the interior angles of a dodecagon( Google it if you have to). A regular polygon has 720 degrees of total angle measures inside. What is the measure of ONE angle inside this polygon? Use your #2 answer. What is the measure of one angle inside this polygon? When you’re done, correct in PEN from the next slide before you pass them in.

Answers: 1. 2. 3. 4. 5. What is the SUM of the interior angles of a regular 15 -gon? S = (15 -2)*180 =>> 13*180 = 2340 degrees How many sides does a regular polygon have with an interior angle sum of 5940 degrees? 5940 = ( n-2)*180 =>> 5940/180 = n-2 =>> 33 = n-2 n = 35, so a 35 -gon Classify a polygon by it’s sides if its interior angle measure is 1260 degrees. 1260 = ( n-2)*180 =>> 1260/180 = n-2 =>> 7 = n-2 n = 9, so a nonagon What is the SUM of the interior angles of a dodecagon. S = (12 -2)*180 =>> 10*180 = 1800 degrees A regular polygon has 720 degrees of total angle measures inside. What is the measure of ONE angle inside this polygon? First, find how many sides: 720=(n-2)*180 =>> 720/180 = n-2 =>> 4 = n-2 =>> n = 6 Now divide total angle measures by sides: 720 degrees divided by 6 sides = 120 degrees for ONE angle. Use your #2 answer. What is the measure of one angle inside this polygon? 5940 / 35 = 169. 7 degrees