Interior and Exterior Angles Formed by Chords Secants

Interior and Exterior Angles Formed by Chords, Secants, and Tangents Lesson 10 -6

Interior Angle Theorem Definition: Angles that are formed by two intersecting chords. A D AEC and DEB are interior angles Interior Angle Theorem: 1 E 2 B C The measure of the angle formed by the two intersecting chords is equal to ½ the sum of the measures of the intercepted arcs. Chapter 10 -6: Interior and Exterior Angles 2

Example: Interior Angle Theorem A 91 C y° x° B D 85 Chapter 10 -6: Interior and Exterior Angles 3

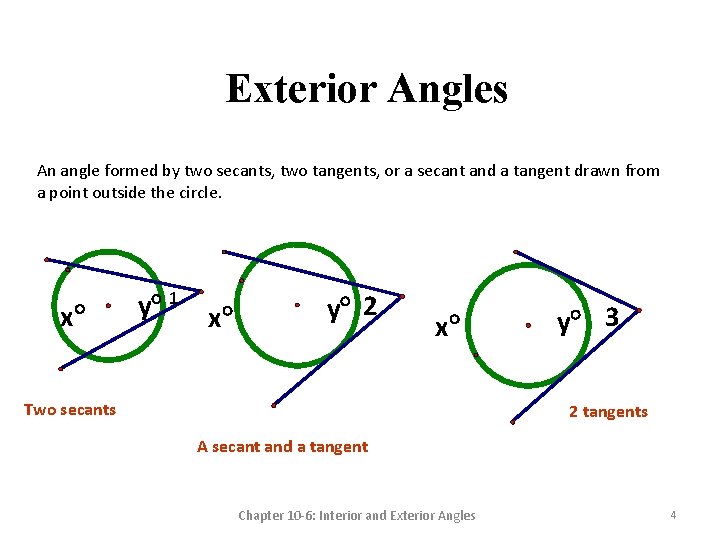
Exterior Angles An angle formed by two secants, two tangents, or a secant and a tangent drawn from a point outside the circle. x y 1 x y 2 x Two secants y 3 2 tangents A secant and a tangent Chapter 10 -6: Interior and Exterior Angles 4

Exterior Angle Theorem The measure of the angle formed is equal to ½ the difference of the intercepted arcs. Chapter 10 -6: Interior and Exterior Angles 5

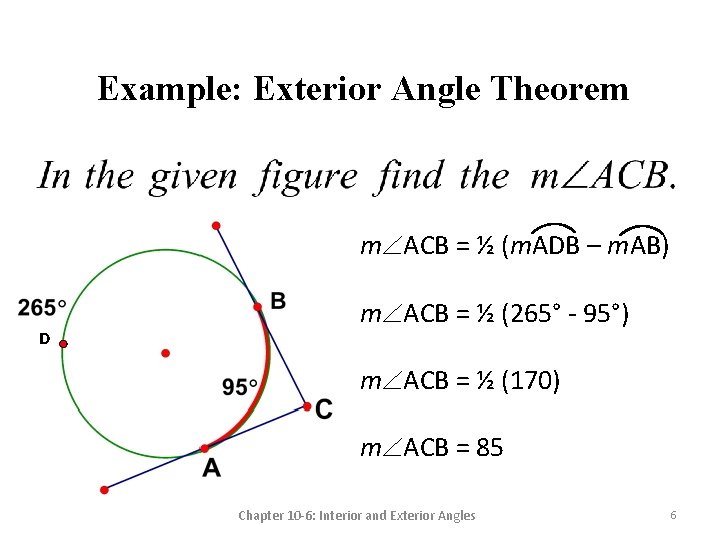
Example: Exterior Angle Theorem m ACB = ½ (m. ADB – m. AB) D m ACB = ½ (265° - 95°) m ACB = ½ (170) m ACB = 85 Chapter 10 -6: Interior and Exterior Angles 6

Given AF is a diameter, m. AG = 100°, m. CE = 30°, and m. EF = 25°. Find the measure of all numbered angles. m 1 = m. FG = 80° D 6 C m 3 ½ (m. CE + m. EF) = 30° E A 3 Q 5 2 1 4 m 2 = m. AG = 100° 25° m 4 ½ (m. GF + m. ACE) = F = 27. 5° = 117. 5° m 5 = 180 ° - 117. 5 ° = 62. 5 ° 100° G m 6 = ½ (m. AG – m. CE) = Chapter 10 -6: Interior and Exterior Angles = 35° 7