Interim Analysis Dr Amit Birajdar 24 09 2015

Interim Analysis Dr. Amit Birajdar 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 1

Outline of seminar • Introduction • Need of interim analysis • Interim analysis & clinical trial • Method of interim analysis • Conclusion 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 2

24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 3

Introduction An interim analysis Ø scientific inferential process (i. e. estimation & hypothesis testing) Ø for the purpose of making a decisions on whether or not to stop a clinical trial early Ø for lack of intended effect or for overwhelming efficacy results in life-threatening & severely debilitating illness. 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 4

Analysis comparing intervention groups at any time before the formal completion of the trial, usually before recruitment is complete. Location Research Question ↓ Clinical Trial ↓ Interim Analysis ↓ Result 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 5

Type of analysis • Administrative Analysis ü Accumulating data in trial are those made purely for the purpose of monitoring the overall progress of a clinical trial. ü Patient enrolment, event rate & safety of drug • Interim Analysis ü formal statistical methods which compare relative treatment group differences. 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 6

Who perform analysis • Independent Data Monitoring Committee • Established by sponsor • Work as per SOP & keep record for review • Independent system 1. control the sharing of information 2. integrity of the clinical trial • Composition: - Trial scientist with statistician • Sponsor a part of it but not interfere at critical situation 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 7

Need of interim analysis • Data dependent stopping or Early stopping • Continuing a trial : - Trial should not continue simply because it was begun. 1. Changes in Inclusion & Exclusion Criteria 2. Accrual Rates 3. Sample Size Adjustment 4. Early Stopping 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 8

• Early interims - review will focus more on safety, quality of conduct and trial integrity rather than efficacy. v 1 st int. analysis - Check the design. v 2 nd int. analysis - Completion of patient enrolment in the centers • Later interims - may include formal efficacy or futility analysis 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 9

Why trial be terminated • Treatment found to convincingly different • Treatment found to convincingly not different • Side effects or toxicities are too severe • Data quality is poor OR Accrual is slow • Definitive information becomes available from an outside source making trial unnecessary or unethical 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 10

• Scientific question is no longer important • Adherence to treatment is low • Trial integrity lowered by fraud or misconduct • Ethical issue • Precision of result • Resource availability 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 11

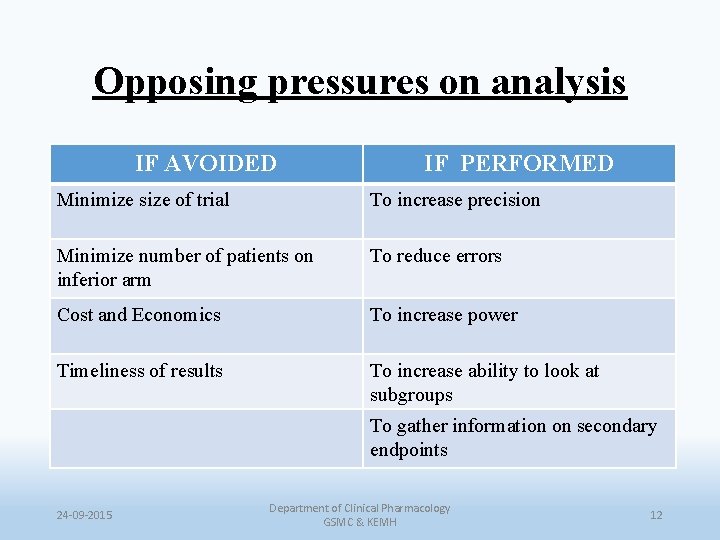
Opposing pressures on analysis IF AVOIDED IF PERFORMED Minimize size of trial To increase precision Minimize number of patients on inferior arm To reduce errors Cost and Economics To increase power Timeliness of results To increase ability to look at subgroups To gather information on secondary endpoints 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 12

Interim analyses in trial Safety/efficacy study (Phase II) v “At this point in time, is there statistical evidence that…. ” ü The treatment will not be as efficacious as we would hope / need it to be ? ü The treatment is clearly dangerous / unsafe ? ü The treatment is very efficacious & we should proceed to a comparative trial ? 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 13

Comparative study (Phase III) v “At this point in time, is there statistical evidence that…. ” ü One arm is clearly more effective than the other? ü One arm is clearly dangerous/unsafe? ü The two treatments have such similar responses that there is no possibility that we will see a significant difference by the end of the trial? 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 14

How to perform analysis Ø Frequentist Approach 1. Multiple Looks 2. Group Sequential Designs • Stopping Boundaries • Alpha Spending Functions 3. Two Stage Designs Ø Likelihood Approach Ø Bayesian Approach 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 15

Multiple looks approach • The false-positive rate is changed because the more occasions the data are reviewed, the greater the opportunity that a large statistical fluctuation may be mistaken for a real effect • Repeatedly testing interim data can inflate false positive error rates if not handled appropriately 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 16

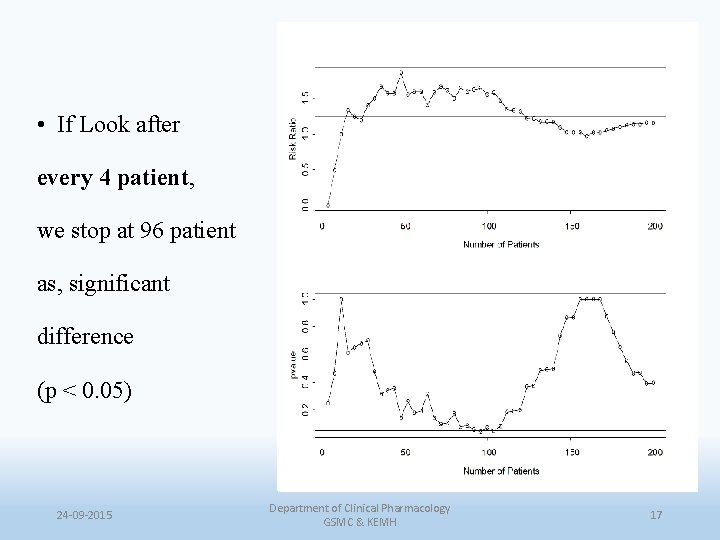
• If Look after every 4 patient, we stop at 96 patient as, significant difference (p < 0. 05) 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 17

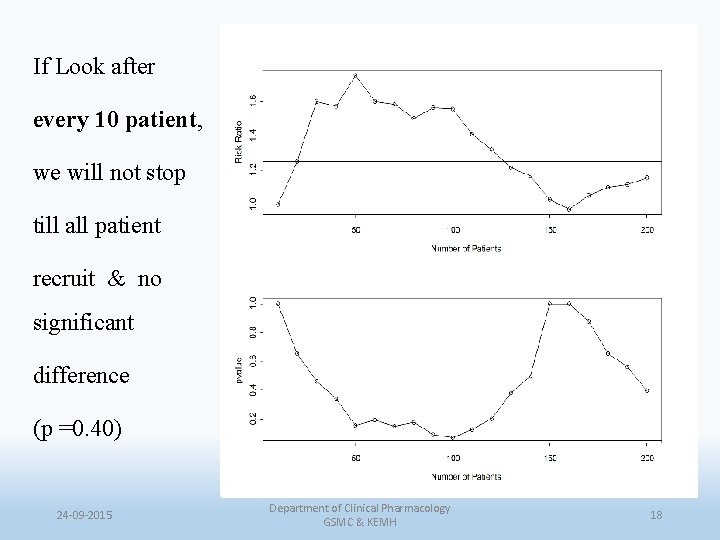
If Look after every 10 patient, we will not stop till all patient recruit & no significant difference (p =0. 40) 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 18

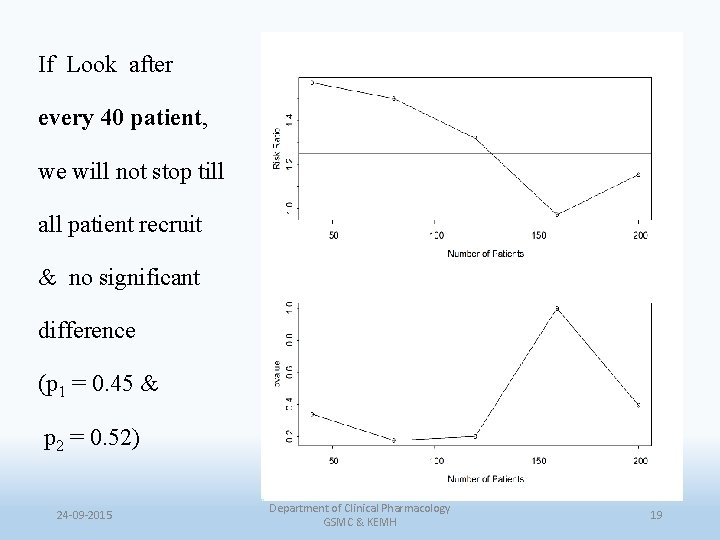
If Look after every 40 patient, we will not stop till all patient recruit & no significant difference (p 1 = 0. 45 & p 2 = 0. 52) 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 19

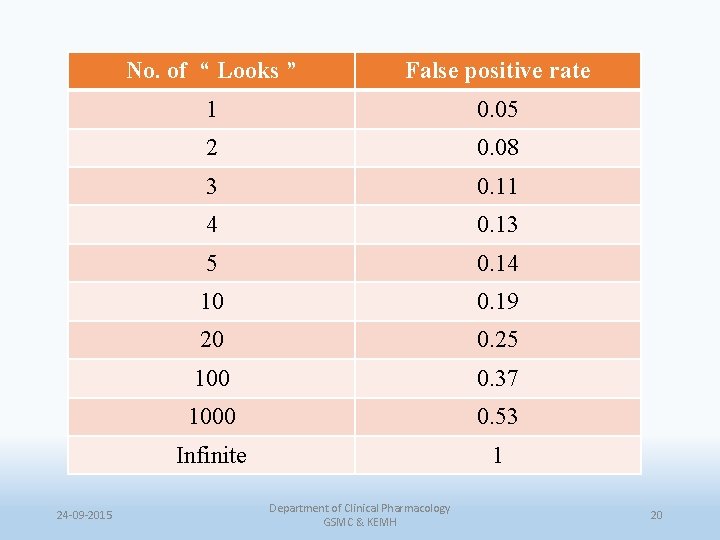
24 -09 -2015 No. of “ Looks ” False positive rate 1 0. 05 2 0. 08 3 0. 11 4 0. 13 5 0. 14 10 0. 19 20 0. 25 100 0. 37 1000 0. 53 Infinite 1 Department of Clinical Pharmacology GSMC & KEMH 20

Mess created by early look • Every time we look at the data and consider stopping, we introduce the chance of falsely rejecting the null hypothesis (chance of a type 1 error) • Under the true null hypothesis and just 2 looks at the data, then we “approximate” the error rates as: § Probability stop at 1 st look: 0. 05 § Probability stop at 2 nd look: 0. 95*0. 05 = 0. 0475 Total probability of stopping = 0. 0975 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 21

Group Sequential Designs § α [PT ] ( “ alpha per test ” ) Test wise alpha § α [PF] ( “ alpha per family of tests ” ) Family wise or experiment wise alpha. 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 22

Sidak inequality • Two independent events, Probability of making one or more Type 1 error on family of test is = 1−(1−α) c which we can also write it as, α[PF] = 1−(1−α[PT ]) c α[PT ] = 1−(1−α[PF]) 1/c • When they are dependent, it gives a lower bound. , α[PF] ≤ 1−(1−α[PT ]) c α[PT ] ≥ 1−(1−α[PF]) 1/c. Department of Clinical Pharmacology 24 -09 -2015 GSMC & KEMH 23

• Šidàk equation involves a fractional power, it is difficult to compute by hand. ↓ • Very close to each other but Bonferroni approximation is pessimistic. • Easier to compute. α[PT ] ≈α[PF] /c • The Šidàk-Bonferroni equations - used to find the value of α[PT ]when α[PF] is fixed. 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 24

• Splitting up α[PF] with unequal slices, • Allocate unequally α[PF] depending upon importance • An unequal allocation of α[PT ]can also be achieved using Šidàk in-equality, but it is more complicated in calculation. Armitage-Mc. Pherson 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 25

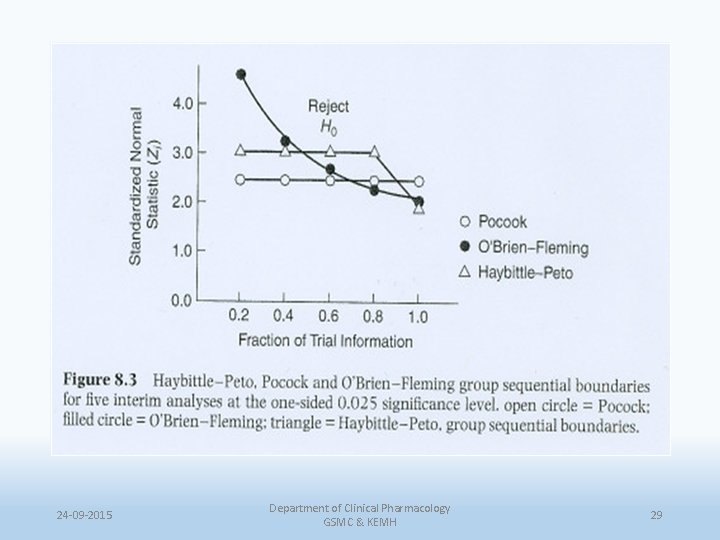
Pocock method • Fixed nominal approach • Recommended for 4/5 interim analysis • Large proportion of alpha spent each time • Uses the same cut off both for the interim and final analysis • Hence, no longer used. • Z(k) = Zp for all k = 1, 2, …, K 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 26

O’Brien & Fleming method • An initial strict cut off which relaxes over a period of time. • But stopping early becomes difficult, because a large part of alpha is saved upto the end • Z(k) = Zobf /(K/k). 1. Boundaries would not cause the sample size to be increased beyond already planned. 2. Boundaries are conservative in that early results must be extreme before early termination would be suggested 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 27

Haybittle-Peto method • Same threshold used at every int. analysis • Final analysis is performed using p=0. 05 which makes easier for investigator & reader to understand. But, • Too much conservative & makes it too difficult to stop a trial. 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 28

24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 29

Drawback • Number of interim tests which will be conducted is specified in advance. • Equal number of individuals enrolled between interim analyses. 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 30

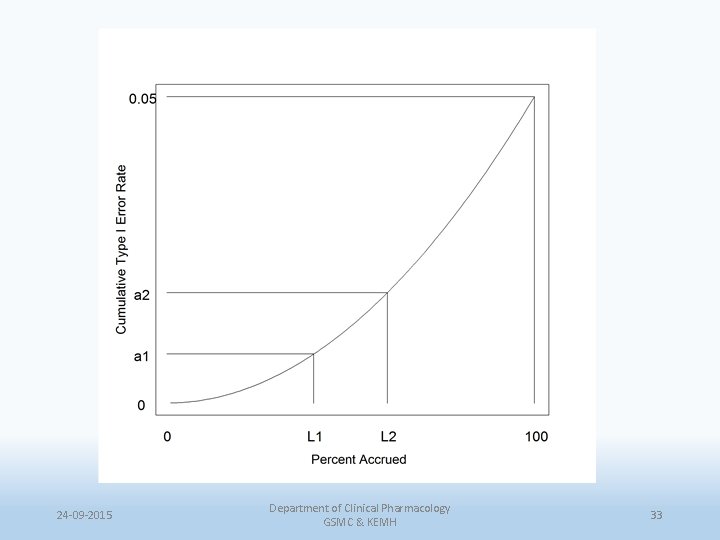
Alpha spending functions • The total alpha is distributed or ‘spent’, over the K interim analyses. • The alpha spending function is a way of describing the rate at which the total alpha is spent as a continuous function of information fraction and thus induces a corresponding boundary. But, • It could be abused by changing the frequency of the analysis as the results came closer to the boundary. 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 31

• Slud & Wei model Not describe as a continuous function of information & no flexibility of structure • Lan & Demets model Flexible group sequential procedure • Proschan By abusing use of a spending function, inflation of will be double only But, Current trend don’t inflate that much. 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 32

24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 33

Advantage • With the α-spending function, number or exact timing of interim analyses need not to be specified in advance. • The approach lends itself well to the accommodation of irregular, unpredictable, and unplanned interim analyses 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 34

Curtailment • Simple Curtailment: A study is stopped as soon as result is inevitable (i. e. it could not be reversed) • Stochastic Curtailment: A study is stopped as soon as result is highly probable given current data • In stochastic curtailment framework, a decision to continue or terminate study at each interim look is based on likelihood of observing positive or negative treatment effect if continued to planned end. 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 35

Power • Conditional Power is the probability of rejecting a false null hypothesis at the end of the study given the data that have emerged so far. • Predicted Power is the average conditional power, averaged over the effect size. • Power indicate whether a study produce useful result • Low power: futile study (High futility index) 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 36

Conditional Power • Stochastic Curtailing refers to a decision to terminate a trial based on CP • Very low power implies that a trial is unlikely to reach statistical significance even if there is a true effect. • One should never begin trial with low power. • The CP should be low to provide sufficient supporting evidence to stop early. • There is no standard threshold in practice • 10% - 30% is the routine acceptable Department of Clinical Pharmacology 24 -09 -2015 GSMC & KEMH 37

• Stochastic curtailment – frequentist method • Predictive power – Partially Bayesian methods • Predictive probability – fully Bayesian methods 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 38

• Positive stopping (i. e. , stopping due to overwhelming evidence of efficacy) O'Brien - Fleming or Peto-Haybittle • Negative stopping (i. e. , stopping for lack of efficacy) stochastic curtailment or conditional power approaches 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 39

Likelihood Approach • Based purely on the likelihood function. • Used test hypotheses & summarize evidence • H 0 = Null hypothesis • H 1 = Alternate hypothesis • Likelihood ratio is given as 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 40

Likelihood ratio test • The numerator - maximum likelihood of an observed outcome under the null hypothesis. • The denominator - maximum likelihood of an observed outcome varying parameters over the whole parameter space. • The numerator of this ratio is less than the denominator ( 0 to 1) • Value’s inference is exactly like p value. 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 41

Sequential probability ratio test ( SPRT ) • Threshold are simply two parallel line with slope log (θ 1/θ 2) • Sampling should stop when the some of sample makes an excursion outside continue sample region. • Extension of the SPRT – Max SPRT 1. Allow composite, one-sided alter. hypothesis 2. Introduction of an upper stopping boundary. 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 42

Wilks's theorem • If the distribution of LR - null & alternative hypothesis. (to accept/reject null hypothesis) • In most case, exact distribution of the likelihood ratio corresponding to specific hypotheses is very difficult to determine. • Sample size approaches infinite & x 2 (Chi square) distribution. • Likelihood ratio A • Compare -2 log(A) to x 2 (Chi square) value. • P value significance 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 43

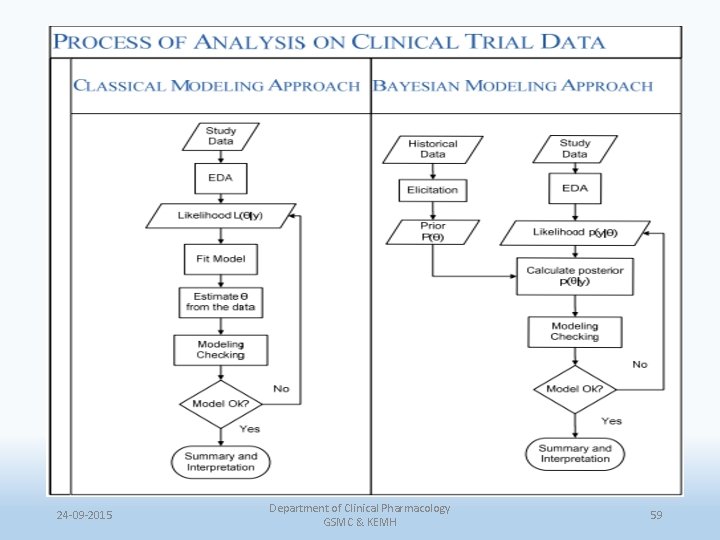
Bayesian approach • Valuable way to manage uncertainty in clinical trial design & analysis. • One key advantage is the ability to incorporate quantitative prior information to support calculations and decision making. • The posterior distribution is then used as the basis for statistical inference. • Any prior information about the treatment effect - whether gained from previous trials or from expert opinions - can be accounted for in a power calculation 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 44

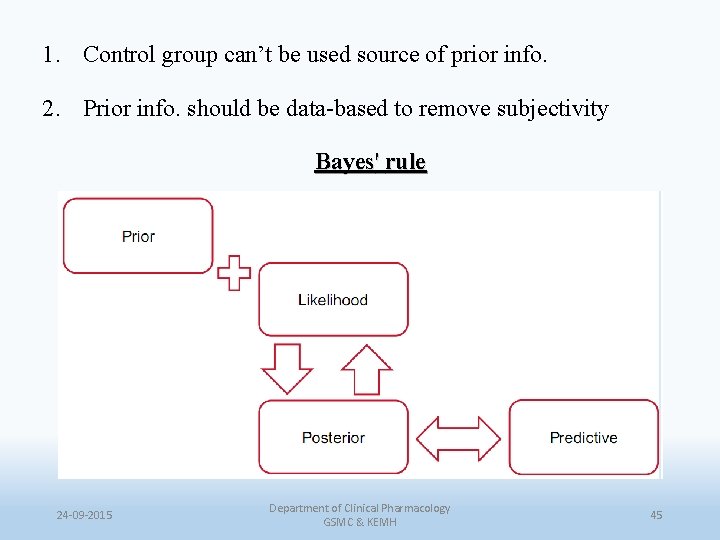
1. Control group can’t be used source of prior info. 2. Prior info. should be data-based to remove subjectivity Bayes' rule 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 45

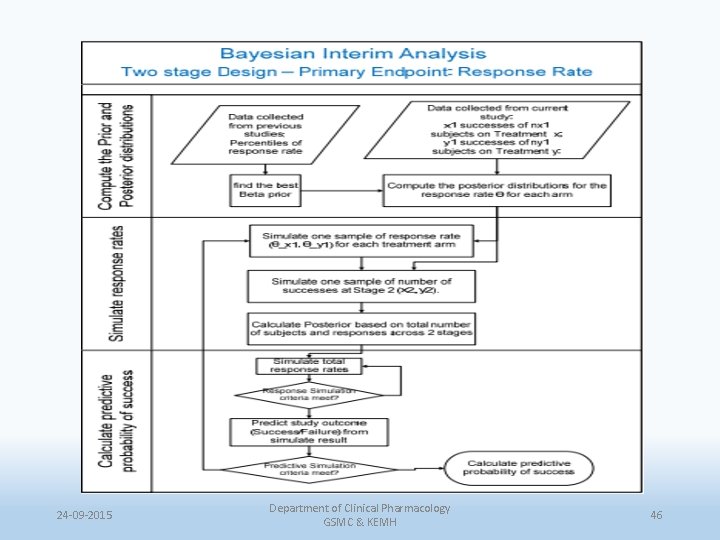
24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 46

Parameter • Posterior distribution of the parameter P(θ/X). • Prior distribution P(θ) • Likelihood function P(X/θ) P(θ/X)~P(X/θ)P(θ) 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 47

Take a study design, 20 subjects in Stage 1 & Stage 2 of each. In Stage 1, 4 responders out of 20 subjects (20%). ( Prior distribution – Beta (1, 1) response rate θ ) Posterior at Stage 1 become: θ/x ~ Beta (1 + 4, 1 + 20 - 4) = Beta ( 5, 17 ) 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 48

In Stage 2, 5 responders in 20 subjects (25%). (Prior distribution – θ ~ Beta (5, 17). ) Now, incorporating the data from Stage 2, Final posterior of θ: θ/x ~ Beta (5 + 5, 17 + 20 - 5) = Beta ( 10, 32 ) 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 49

• This is the same result as would have been obtained from a full data analysis, rather than the separate stage calculations as has been used above • In that case, Prior distribution remains : θ ~ Beta (1, 1) Taking the full data into account (Stage 1 & Stage 2) 9 responses out of 40 subjects • Posterior of : Beta (1 + 9, 1 + 40 – 9 ) = Beta ( 10, 32 ) 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 50

Treatment of Kidney Cancer • Suppose we have n = 40 patients who will be receiving an experimental therapy which is believed to be better than current treatments which historically have had a 5 -year survival rate of 20%, i. e. the probability of 5 -year survival is p = 0. 20 • Thus the number of patients out of 40 in our study surviving at least 5 years has a binomial distribution, i. e. X ~ BIN(40, 0. 20). 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 51

• If X ~ BIN(n, p), then • where 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 52

• X ~ BIN(40, . 20), find the probability that exactly 16 patients survive at least 5 years • This requires some calculator gymnastics and some scratch work. • Also, keep in mind we need to find the probability of having 16 or more patients surviving at least 5 yrs. • P(X > 16) = P(X = 16) + P(X = 17) + P(X =40) =. 002936 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 53

FDA Guidelines 1. Prospectively designed 2. Restricted to studies that can utilize good data-based prior info. 3. Validity of its prior info. 4. Conducted such that the control group cannot be used as a source of prior info. 5. Simulations are important to approximate size of the trial and the strategy of interim looks in order. Because, Studies are not a fixed size. 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 54

• Bayesian analytical method : 1. Posterior distribution summaries 2. Interval estimation 3. Predictive probability approach 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 55

Post. distribution summary • Posterior mean : The posterior mean is compromise between prior distribution & observed data E(θ/x)=∫θP(θ/x)dθ Beta (a, b) mean E(X) =a/(a+b). Posterior mean of Beta (10, 32) is 10/42. • Posterior mode : The posterior mode is ‘most likely’ posterior value given prior distribution. If , X~ Beta (a, b), if a, b > 1, mode is: Posterior mode of Beta (10, 32) is 9/40 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 56

Interval estimation • Credible intervals are used for purposes similar to those of confidence intervals in frequentist statistics. • Confidence intervals: P(a(x)< θ<b(x)| θ)=1 -α, x is the random variable and θ is unknown • Credible intervals: P(a(x)< θ <b(x)| x)=1 -α, θ is the random variable given the data x • The Bayesian Credible Interval represents a posterior probability interval that can be used for interval estimation. 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 57

Predictive probability approach This approach can be used to predict a future data point on the basis of a currently observed data x. 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 58

24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 59

Unplanned interim analysis • Unplanned interim analysis should avoid • But un-avoidable 1. Study report must carefully explain need of analysis 2. Broken degree of blindness 3. Subsequent action • Ad-hoc approach • Alpha spending function approach • When data look interesting 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 60

Conclusion • Depending upon study design and need of trial, statistician should use appropriate interim analysis. • Recently approach of interim analysis is trending toward Likelihood & Bayesian approach. • Adaptive study design demands requires adaptive alpha value. 24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 61

24 -09 -2015 Department of Clinical Pharmacology GSMC & KEMH 62