Interference of Waves Interference The Michelson interferometer Crossed

Interference of Waves Interference The Michelson interferometer Crossed beams Standing waves Prof. Rick Trebino Georgia Tech www. frog. gatech. edu Boundary conditions

How do humans localize sound? How do you know that a sound occurs on one side? How about if it occurs on the other side? How about if it’s in front of you? But what about if it’s above you or behind you? And why does sound from headphones seem to be inside your head?

Interference involves the sum of two or more waves. Opals use interference between tiny structures to yield bright colors. It’s all about the relative phase of the waves.

Superposition means that waves pass through each other unchanged. Otherwise they'd get screwed up while overlapping. So interference is easy. Just add up the waves involved. This is because the sum of solutions to the wave equation is also a solution.

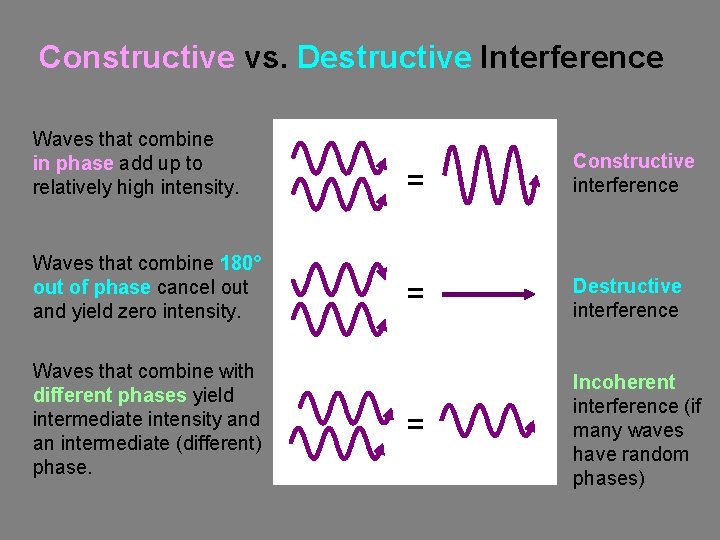
Constructive vs. Destructive Interference Waves that combine in phase add up to relatively high intensity. = Constructive interference Waves that combine 180° out of phase cancel out and yield zero intensity. = Destructive interference = Incoherent interference (if many waves have random phases) Waves that combine with different phases yield intermediate intensity and an intermediate (different) phase.

Newton's Rings

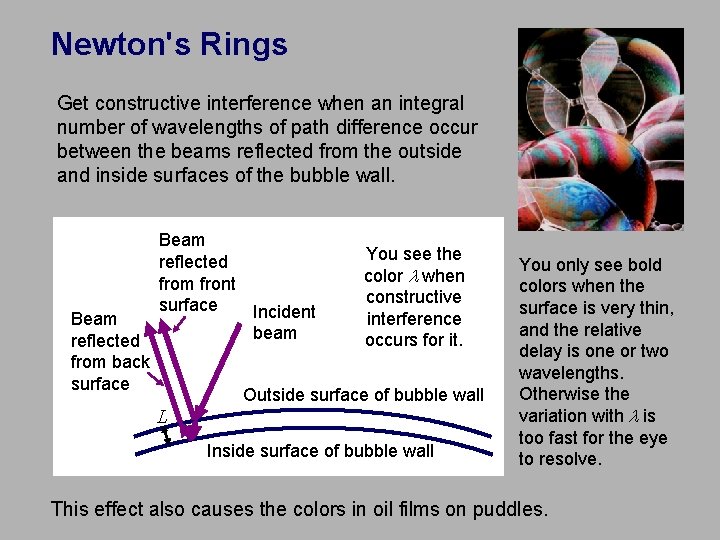
Newton's Rings Get constructive interference when an integral number of wavelengths of path difference occur between the beams reflected from the outside and inside surfaces of the bubble wall. Beam You see the reflected color l when from front constructive surface Incident interference Beam beam occurs for it. reflected from back surface Outside surface of bubble wall L Inside surface of bubble wall You only see bold colors when the surface is very thin, and the relative delay is one or two wavelengths. Otherwise the variation with l is too fast for the eye to resolve. This effect also causes the colors in oil films on puddles.

Anti-Reflection Coatings Notice that the center of the round glass plate looks like it’s missing. It’s not! There’s an interference-based antireflection coating there (on both the front and back of the glass). Such coatings have been common on photography lenses and are now common on eyeglasses. Even my new watch is ARcoated!

Photonic crystals use interference to guide light—sometimes around corners! Borel, et al. , Opt. Expr. 12, 1996 (2004) Yellow indicates peak field regions. Augustin, et al. , Opt. Expr. , 11, 3284, 2003. Interference controls the path of light. Constructive interference occurs along the desired path. Destructive interference occurs elsewhere.

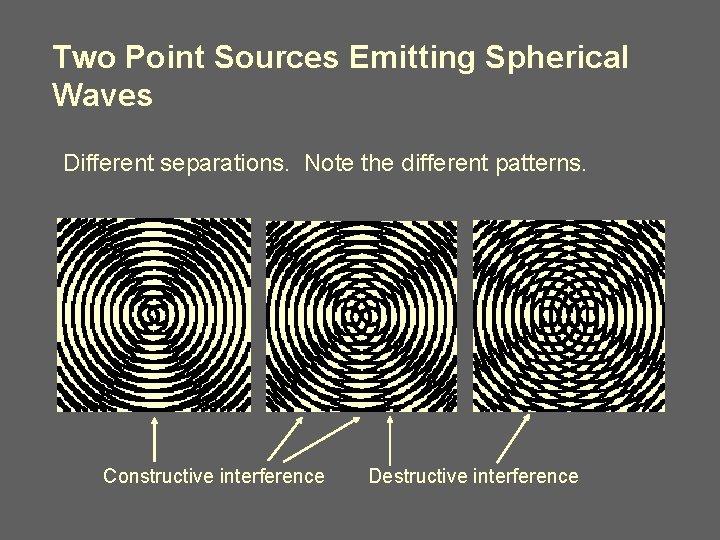
Two Point Sources Emitting Spherical Waves Different separations. Note the different patterns. Constructive interference Destructive interference

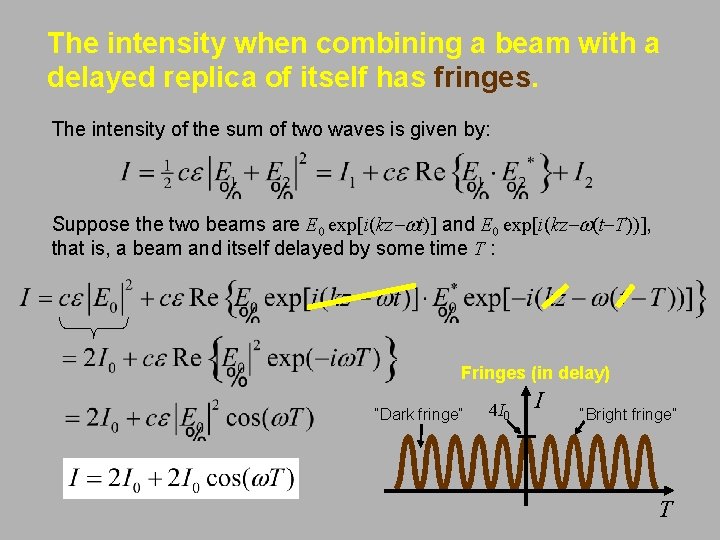
The intensity when combining a beam with a delayed replica of itself has fringes. The intensity of the sum of two waves is given by: Suppose the two beams are E 0 exp[i(kz-wt)] and E 0 exp[i(kz-w(t-T))], that is, a beam and itself delayed by some time T : Fringes (in delay) “Dark fringe” 4 I 0 I “Bright fringe” T

A delay in time is also a delay in space. Propagation by a distance L is a delay in time, T = L/c. We can think of the phase delay in terms of time or space: Simply moving a mirror can vary the delay of a beam by many wavelengths. Moving a mirror backward by a distance L yields a delay of: Mirror Input beam E(t) Output beam E(t–T) Translation stage Do not forget the factor of 2! Light must travel the extra distance to the mirror—and back! Since light travels 300µm per ps, 300µm of mirror displacement yields a delay of 2 ps. Such delays can come about naturally, too.

Albert Michelson In the 1870’s Albert Michelson invented the interferometer now named after him to measure the speed of light and its properties. Albert Michelson 1852– 1931

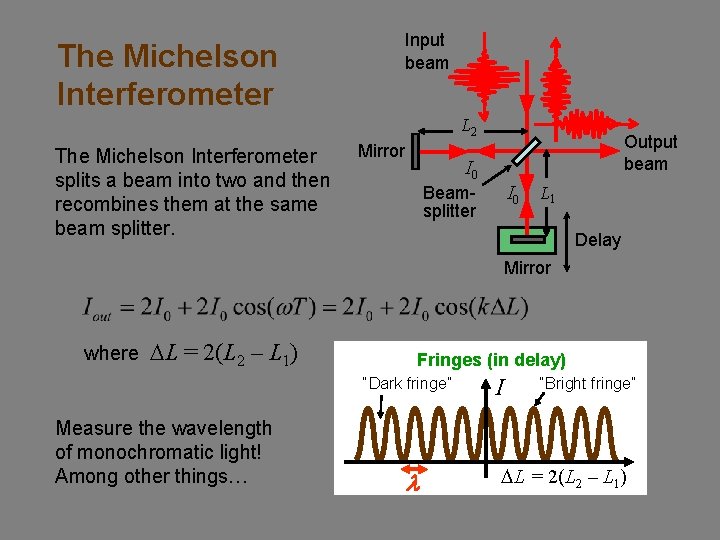
Input beam The Michelson Interferometer L 2 The Michelson Interferometer splits a beam into two and then recombines them at the same beam splitter. Mirror Output beam I 0 Beamsplitter L 1 Delay Mirror where DL = 2(L 2 – L 1) Fringes (in delay) “Dark fringe” Measure the wavelength of monochromatic light! Among other things… l I “Bright fringe” DL = 2(L 2 – L 1)

Now we’ll add waves with different complex exponentials. It's easy to add waves with the same complex exponentials. where all initial phases are lumped into E 1, E 2, and E 3. ~ ~ ~ But sometimes the complex exponentials will be different! Note the plus sign!

Recall that a wave can propagate in any direction in space. Recall the 3 D wave equation: or which has the solution: where and

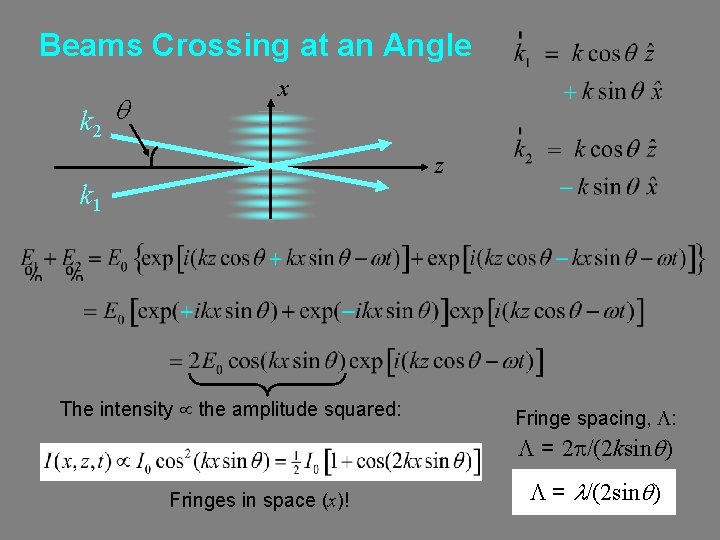
Beams Crossing at an Angle k 2 q x z k 1 The intensity the amplitude squared: Fringe spacing, L: L = 2 p/(2 ksinq) Fringes in space (x)! L = l/(2 sinq)

Big angle: small fringes. Small angle: big fringes. The fringe spacing, L: As the angle decreases to zero, the fringes become larger and larger, until finally, at q = 0, the intensity pattern becomes constant. x Large angle: Small angle: L = 0. 1 mm is about the minimum fringe spacing you can see: very small!

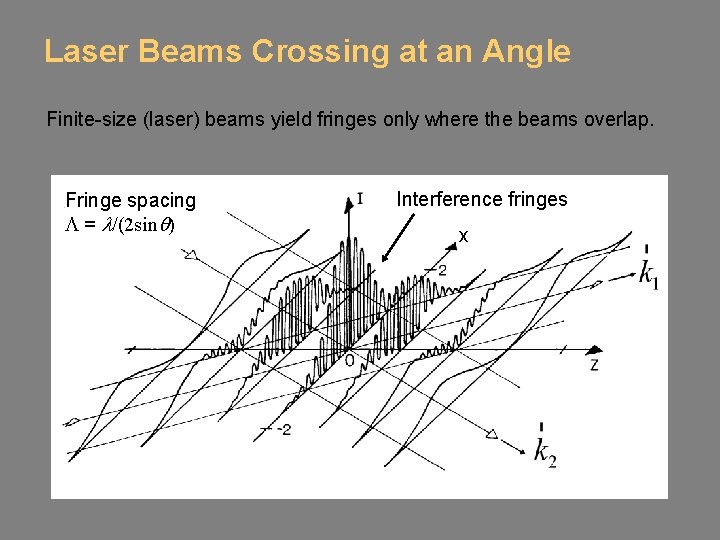
Laser Beams Crossing at an Angle Finite-size (laser) beams yield fringes only where the beams overlap. Fringe spacing L = l/(2 sinq) Interference fringes x

Pulsed Waves Crossing at an Angle

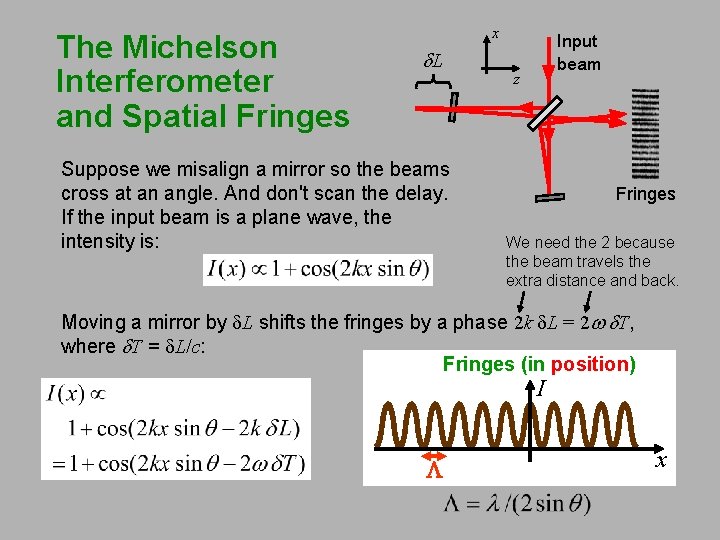
The Michelson Interferometer and Spatial Fringes x d. L Suppose we misalign a mirror so the beams cross at an angle. And don't scan the delay. If the input beam is a plane wave, the intensity is: Input beam z Fringes We need the 2 because the beam travels the extra distance and back. Moving a mirror by d. L shifts the fringes by a phase 2 k d. L = 2 w d. T, where d. T = d. L/c: Fringes (in position) I L x

Mirror 0 Counter-Propagating Waves z Suppose a wave reflects off a mirror. This generates counter-propagating waves, that is, waves propagating in opposite directions. This is the case: q = 90º. Add together counter-propagating sine waves: Re{-i. E 0 exp(kz ±wt)} sinq = 1 Note that the intensity peaks will still be separated by l/2 sinq, or l/2.

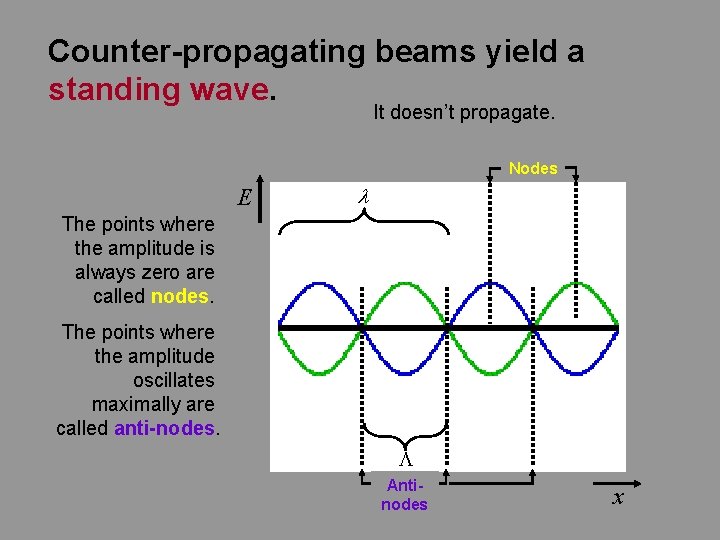
Counter-propagating beams yield a standing wave. It doesn’t propagate. Nodes E l The points where the amplitude is always zero are called nodes. The points where the amplitude oscillates maximally are called anti-nodes. L Antinodes x

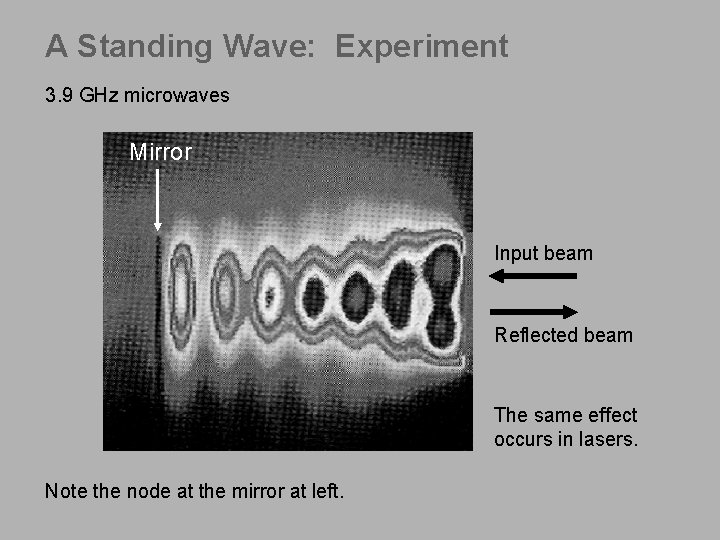
A Standing Wave: Experiment 3. 9 GHz microwaves Mirror Input beam Reflected beam The same effect occurs in lasers. Note the node at the mirror at left.

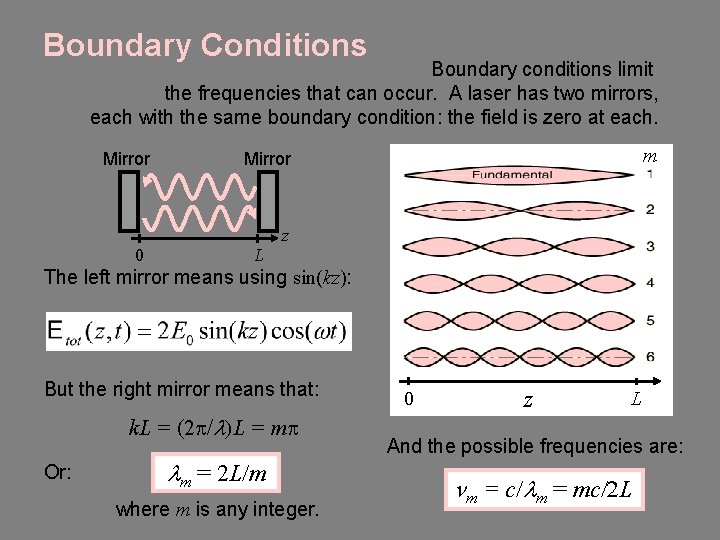
Boundary Conditions Boundary conditions limit the frequencies that can occur. A laser has two mirrors, each with the same boundary condition: the field is zero at each. Mirror 0 m Mirror L z The left mirror means using sin(kz): But the right mirror means that: k. L = (2 p/l)L = mp Or: lm = 2 L/m where m is any integer. 0 z L And the possible frequencies are: nm = c/lm = mc/2 L

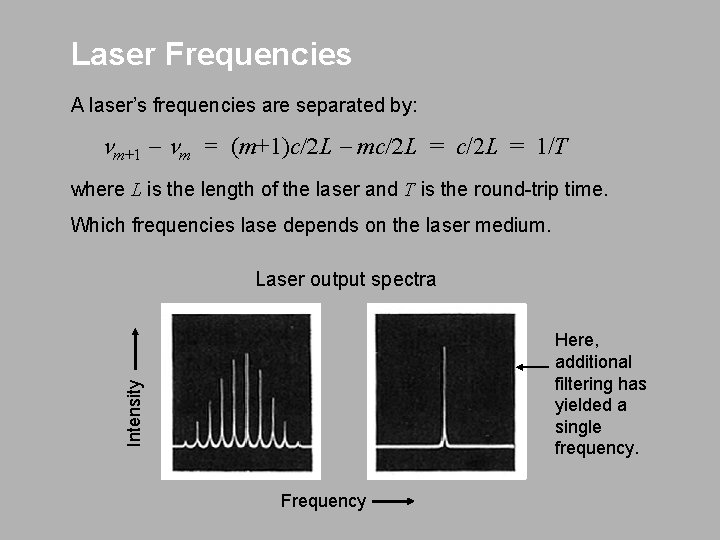
Laser Frequencies A laser’s frequencies are separated by: nm+1 - nm = (m+1)c/2 L - mc/2 L = 1/T where L is the length of the laser and T is the round-trip time. Which frequencies lase depends on the laser medium. Laser output spectra Intensity Here, additional filtering has yielded a single frequency. Frequency

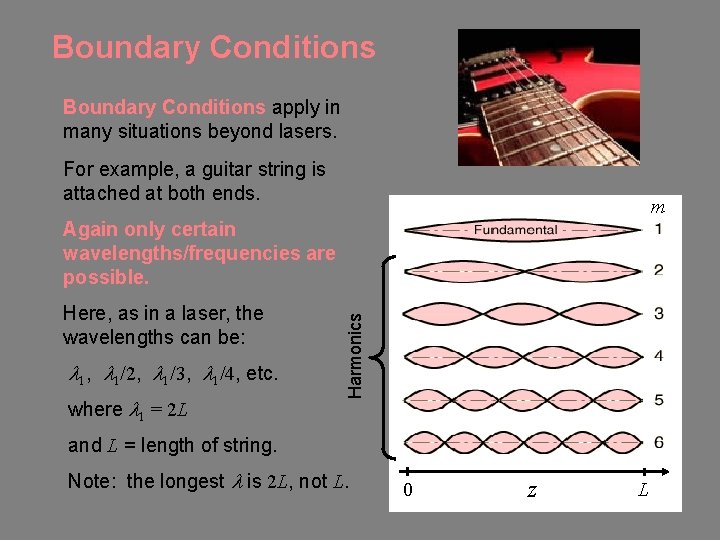
Boundary Conditions apply in many situations beyond lasers. For example, a guitar string is attached at both ends. m Here, as in a laser, the wavelengths can be: l 1, l 1/2, l 1/3, l 1/4, etc. where l 1 = 2 L Harmonics Again only certain wavelengths/frequencies are possible. and L = length of string. Note: the longest l is 2 L, not L. 0 z L

The Fundamental and Harmonics in Musical Instruments Musical instruments that use strings can vary their pitch (frequency) by using strings of different length. The fundamental frequency is what we interpret as the pitch, but many higherfrequency harmonics are also present. Different instruments have different higher harmonics. The harmonics give the instrument its character.

The names we use for notes reflect this effect. For example, “A” corresponds to many equally spaced keys. The same is true for other notes.

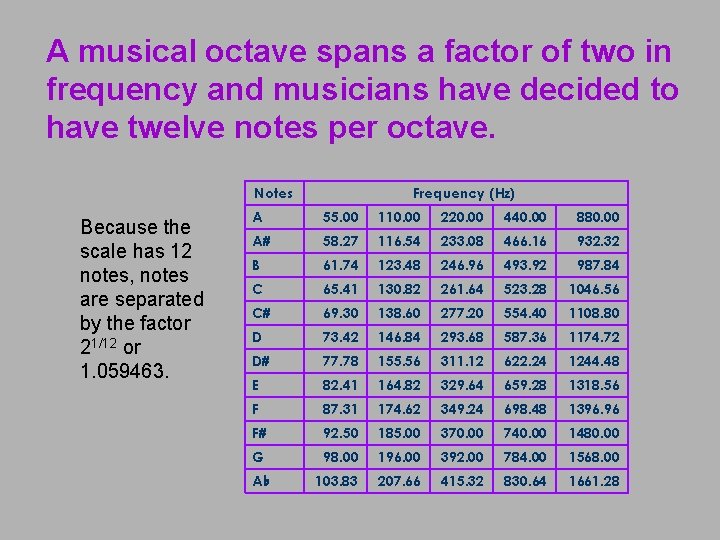
A musical octave spans a factor of two in frequency and musicians have decided to have twelve notes per octave. Notes Because the scale has 12 notes, notes are separated by the factor 21/12 or 1. 059463. Frequency (Hz) A 55. 00 110. 00 220. 00 440. 00 880. 00 A# 58. 27 116. 54 233. 08 466. 16 932. 32 B 61. 74 123. 48 246. 96 493. 92 987. 84 C 65. 41 130. 82 261. 64 523. 28 1046. 56 C# 69. 30 138. 60 277. 20 554. 40 1108. 80 D 73. 42 146. 84 293. 68 587. 36 1174. 72 D# 77. 78 155. 56 311. 12 622. 24 1244. 48 E 82. 41 164. 82 329. 64 659. 28 1318. 56 F 87. 31 174. 62 349. 24 698. 48 1396. 96 F# 92. 50 185. 00 370. 00 740. 00 1480. 00 G 98. 00 196. 00 392. 00 784. 00 1568. 00 A♭ 103. 83 207. 66 415. 32 830. 64 1661. 28

Two-Dimensional Boundary Conditions For a rectangular region, the wave is a product of the waves in the x and y directions. For a boundary in which the wave must be zero at x = y = 0, x = Lx, and y = Ly, we have: /Ly /Lx Note the 2’s. where sin’s force f(0, 0) = 0. Also: kx = 2 mxp/(2 Lx), and ky = 2 myp/(2 Ly), where mx and my are integers, so f(Lx, Ly) = 0.

Drums have round two-dimensional boundaries and so exhibit 2 D standing waves with similar wavelength limitations.

Boundary conditions rule! In all wave problems, a differential wave equation describes what shapes the waves could have. The boundary conditions determine limit which wavelengths can actually occur. Even light waves (recall that plane waves exist all over space and so aren’t realistic) have the boundary condition that they’re zero at infinity. Additional effects can further limit the observed wavelengths.

Diffraction Gratings A diffraction grating is an object with periodic optical properties, for example, grooves. Diffraction gratings are important because they spectrally disperse light much more than prisms do. Interestingly, they’re best understood using interference ideas.

Diffraction Gratings Let a plane wave impinge on a periodic array of scatterers, which emit spherical waves (but we’ll approximate them as plane waves in all directions). Constructive interference occurs if the delay between adjacent beamlets is an integral number, m, of wavelengths. Path difference: AB – CD = ml Scatterer D qm C Incident qi wave-front qm a A qi Scatterer where m is any integer. a B Potential diffracted wave-front AB = a sin(qm) CD = a sin(qi) A grating has solutions of zero, one, or many values of m, or orders. And m and qm can be negative, too.

Real Diffraction Gratings m = -1 m=0 m =1 m=2 Diffracted white light White light diffracted by a real grating. Diffraction gratings The dots on a CD are equally spaced (although some are missing, of course), so it acts like a diffraction grating.

World’s Largest Diffraction Grating Lawrence Livermore National Lab