Interference of Sound Waves Principle of Superposition 2

Interference of Sound Waves

Principle of Superposition 2 Waves In The Same Medium: The observed displacement y(x, t) is the algebraic sum of the individual displacements: y(x, t) =y 1(x, t) + y 2(x, t) (for a “linear medium”)

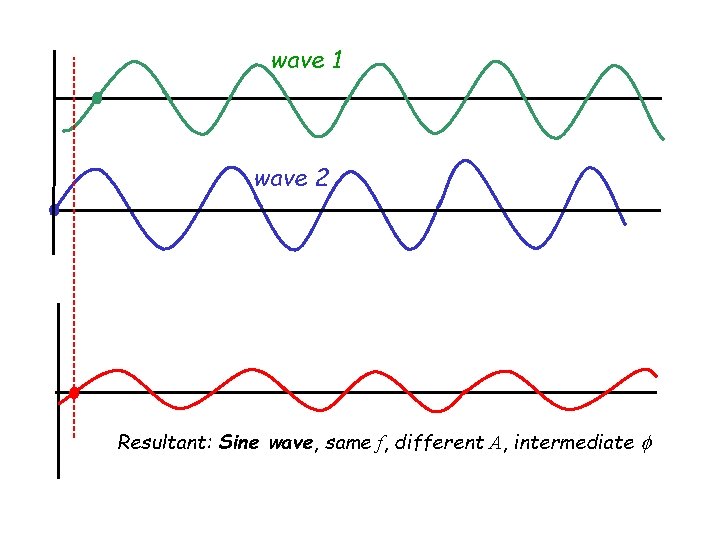
What’s Special about Harmonic Waves? 2 waves, of the same amplitude, same angular frequency and wave number (and therefore same wavelength) traveling in the same direction in a medium but are out of phase: Trig: sin a + sin b = 2 cos [(a-b)/2] sin [(a+b)/2] Result: Resultant amplitude

Assume is positive: For what phase difference is the total amplitude 2 A? For what phase difference is the total amplitude 0? For what phase difference is the total amplitude A/2?

wave 1 wave 2 Resultant: Sine wave, same f, different A, intermediate f

Interference 2 waves, of the same frequency; out of phase. Eg. Then y 1=A 0 sin (kx - wt) y 2=A 0 sin (kx - wt +f) y. R=ARsin(kx-wt+f /2), and the resultant amplitude is AR=2 A 0 cos(½f ). Identical waves which travel different distances will arrive out of phase and will interfere, so that the resultant amplitude varies with location.

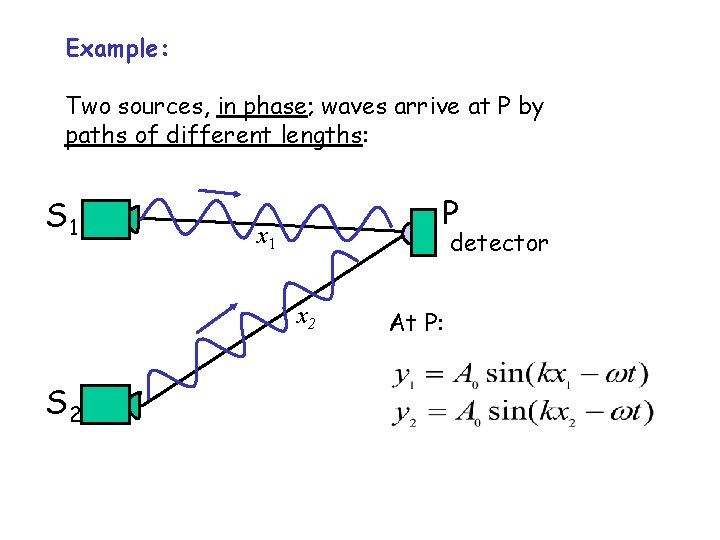
Example: Two sources, in phase; waves arrive at P by paths of different lengths: S 1 P x 1 detector x 2 S 2 At P:

Phase difference : = Define x to be the path difference Then (using trig), at detector: kx terms don’t cancel!

Example A pair of speakers is separated by 3. 0 m and driven by the same oscillator. The listener walks perpendicular from a point on the centerline 8 m away to a distance of 0. 35 m before reaching the first minimum in sound intenstiy. What is the frequency of the oscillator? 3 m 8. 0 m 0. 35 m

Solution

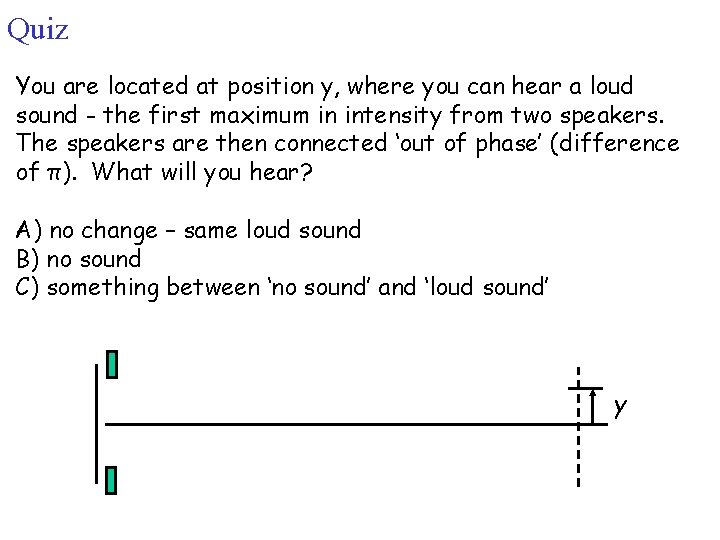
Quiz You are located at position y, where you can hear a loud sound - the first maximum in intensity from two speakers. The speakers are then connected ‘out of phase’ (difference of π). What will you hear? A) no change – same loud sound B) no sound C) something between ‘no sound’ and ‘loud sound’ y

Intensity I I = Power per unit area Units: W / m 2 (the area is measured perpendicular to the wave velocity) Intensity is proportional to (resultant amplitude)2 , since I=P/Area and power is proportional to Amp 2 Two sources, each with amplitude Ao, intensity Io , phase difference f:

Notes: 1) Maximum IR is 4 x IO 2) Maxima when f = 0, 2π, 4π, 6π , … x = 0, ± λ, ± 2λ, … 3) Minima (zero intensity) when f = π, 3π, 5π , … x = ± λ/2, ± 3λ/2, ± 5λ/2, … Note: The sources are in phase !!!

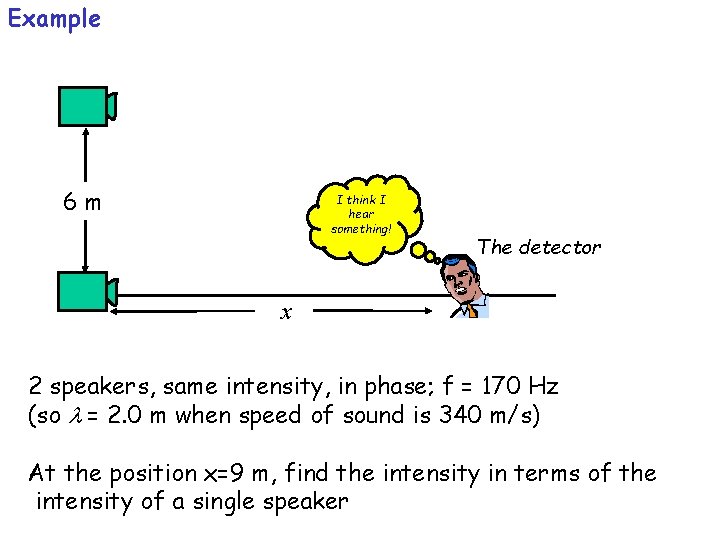
Example 6 m I think I hear something! The detector x 2 speakers, same intensity, in phase; f = 170 Hz (so l = 2. 0 m when speed of sound is 340 m/s) At the position x=9 m, find the intensity in terms of the intensity of a single speaker

Solution