Interference between independent cold atom systems Anatoli Polkovnikov

Interference between independent cold atom systems Anatoli Polkovnikov, Boston University Collaboration: Ehud Altman Eugene Demler Vladimir Gritsev AFOSR - The Weizmann Institute of Science Harvard University Workshop on Quantum Noise in Strongly Correlated Systems. Weizmann Institute, Jan. 2008

Interference between independent sources. (Hanbury-Brown Twiss effect)

Interference between independent sources. (Hanbury-Brown Twiss effect) x 1 Origin of interference – superposition principle. x 2 Interference term drops out for uncorrelated sources Intensity-intensity correlator survives! HBT effect is the classical wave phenomenon!

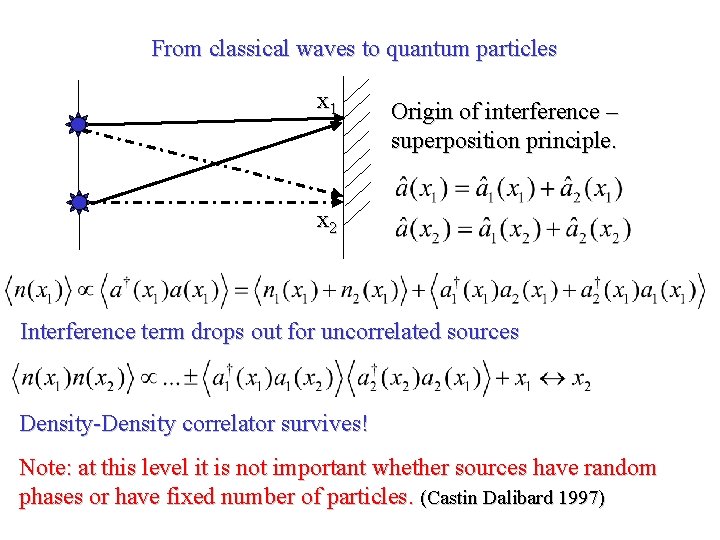
From classical waves to quantum particles x 1 Origin of interference – superposition principle. x 2 Interference term drops out for uncorrelated sources Density-Density correlator survives! Note: at this level it is not important whether sources have random phases or have fixed number of particles. (Castin Dalibard 1997)

Interference between two condensates. TOF d x Free expansion:

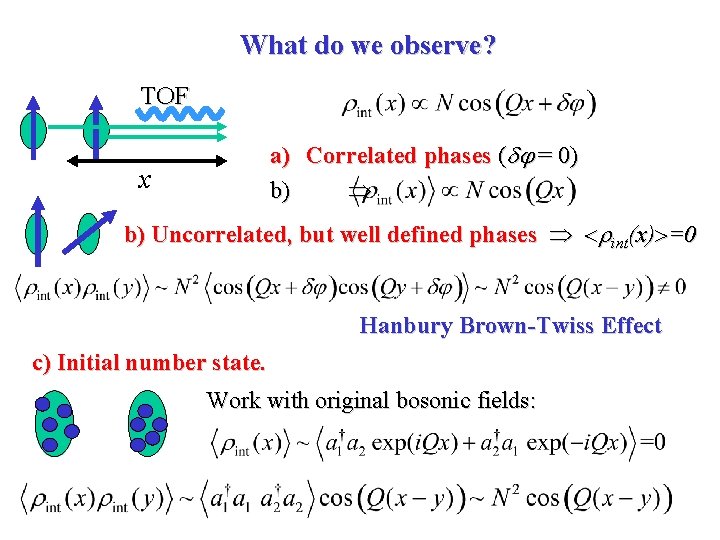
What do we observe? TOF a) Correlated phases ( = 0) b) x b) Uncorrelated, but well defined phases int(x) =0 Hanbury Brown-Twiss Effect c) Initial number state. Work with original bosonic fields:

Define an observable (interference amplitude squared ): depends only on N Shot (counting) noise distinguishes quantum particles from classical waves (only affects fluctuations of the interference amplitude): A. P. 2006 Imambekov, Gritsev, Demler, 2007 The interference amplitude does not fluctuate at large N! Castin, Dalibard 1997.

Interference from multiple sources Having many particles in each condensate does not reduce noise in the interference amplitude. d x Redefine the observable Utilize higher momentum harmonics. Noiseless HBT signal for large number of sources, true both for bosons and for fermions. We can have classical Grassman waves for fermions!

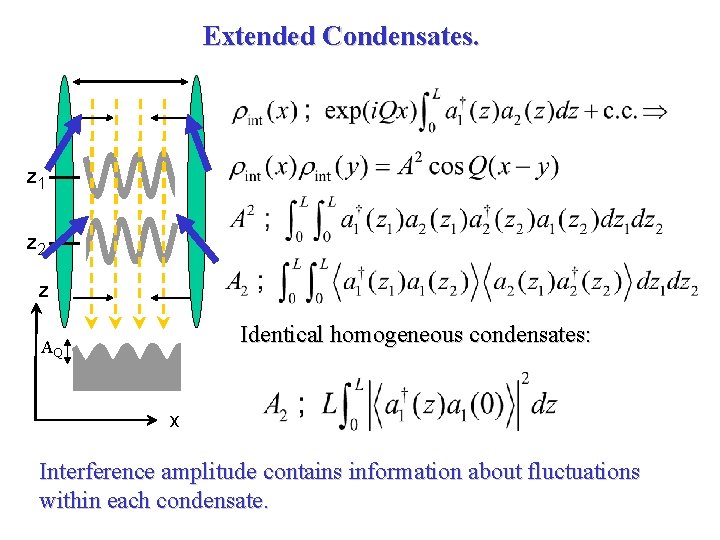
Extended Condensates. z 1 z 2 z Identical homogeneous condensates: AQ x Interference amplitude contains information about fluctuations within each condensate.

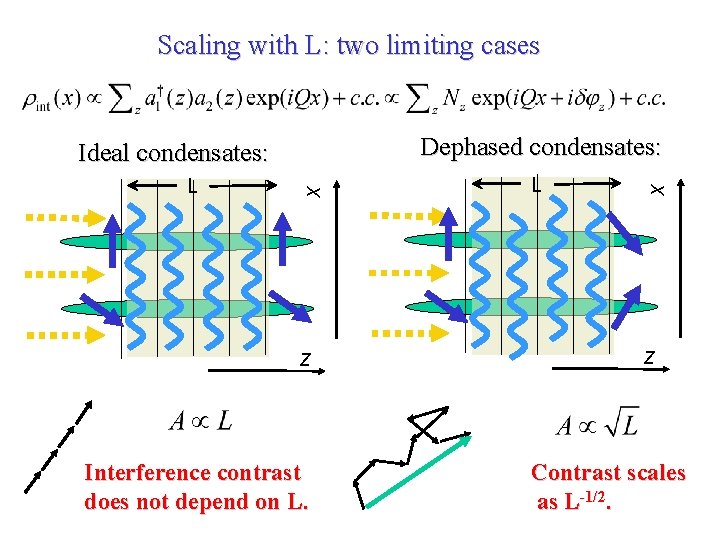
Scaling with L: two limiting cases x L z Interference contrast does not depend on L. L x Dephased condensates: Ideal condensates: z Contrast scales as L-1/2.

Formal derivation: Ideal condensate: L Thermal gas: L

Intermediate case (quasi long-range order). L 1 D condensates (Luttinger liquids): z Repulsive bosons with short range interactions: Finite temperature:

Observing the Kosterlitz-Thouless transition Above KT transition Below KT transition Lx Ly Ly Lx Universal jump of at TKT Always algebraic scaling, easy to detect.

Higher Moments (More in talk by V. Gritsev) is an observable quantum operator Identical condensates. Mean: Similarly higher moments Probe of the higher order correlation functions. Universal (size independent) distribution function: Shot noise contribution: d. A 2 n / A 2 n~ 1 / L 1 -1/K Shot noise is subdominant for K>1 at T=0.

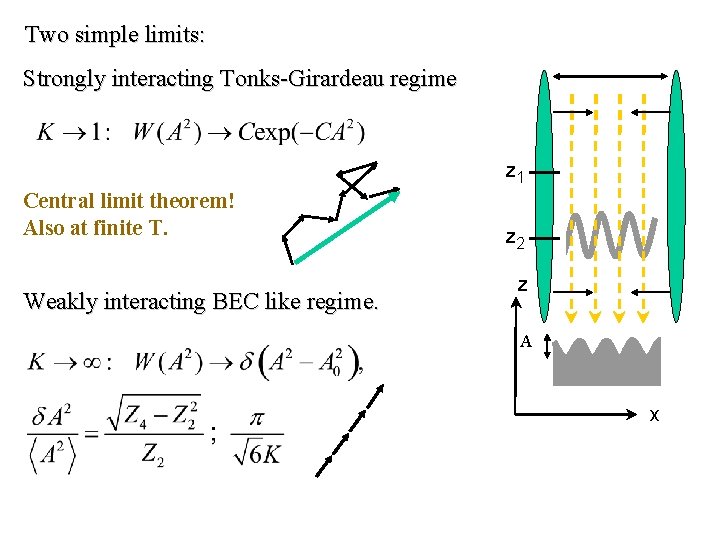
Two simple limits: Strongly interacting Tonks-Girardeau regime z 1 Central limit theorem! Also at finite T. Weakly interacting BEC like regime. z 2 z A x

Connection to the impurity in a Luttinger liquid problem. (more in V. Gritsev talk on Thursday). Experimental simulation of the quantum impurity problem 1. Do a series of experiments and determine the distribution function of the interference amplitude. 2. Evaluate the integral. 3. Read the result.

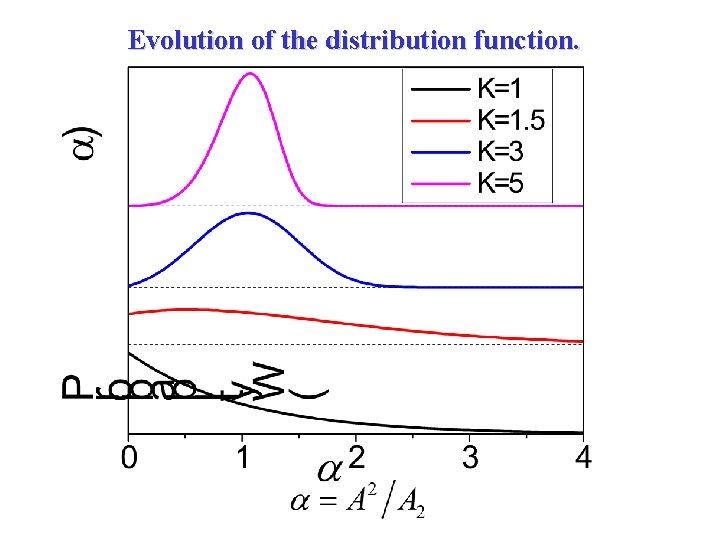
Evolution of the distribution function.

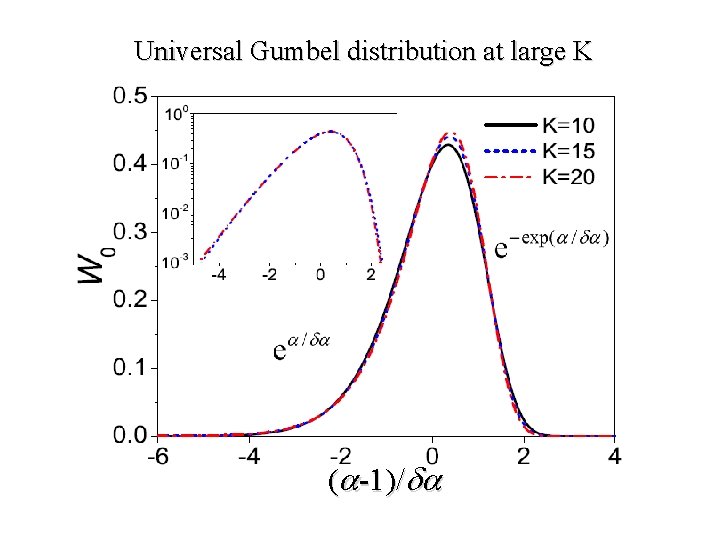
Universal Gumbel distribution at large K ( -1)/

Generalized extreme value distribution: Other examples of extreme value statistics. Emergence of extreme value statistics on other instances: E. Bretin, Phys. Rev. Lett. 95, 170601 (2005) From independent random variables to correlated intervals Also 1/f noise

Detecting fermionic superfluidity (D-wave…) TOF d Before Good for shot noise but not for superfluidity. Now Problem with gauge invariance (undefined relative phase)

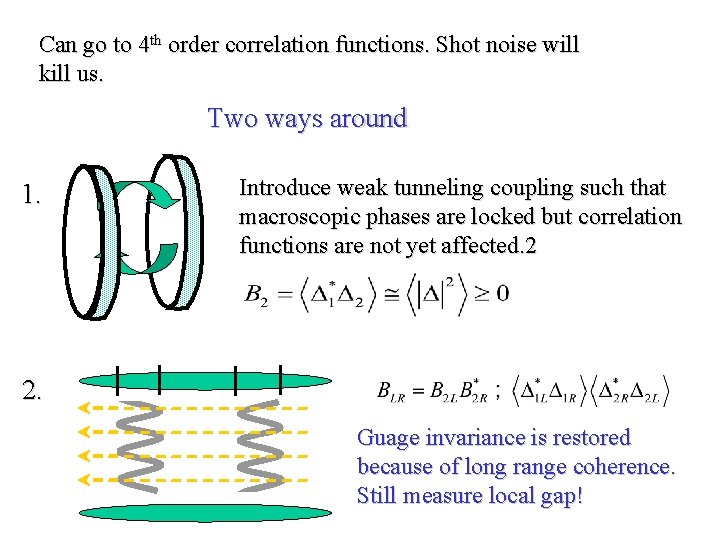
Can go to 4 th order correlation functions. Shot noise will kill us. Two ways around 1. Introduce weak tunneling coupling such that macroscopic phases are locked but correlation functions are not yet affected. 2 2. Guage invariance is restored because of long range coherence. Still measure local gap!

Fermions on a lattice. Different orientations of imaging beams give strong angular dependence of the signal in D-wave case. Can detect even the sign of the pairing gap using two different imaging beams for BL and BR and having one D-condensate and one S-condensate.

Conclusions. Two sources of noise in the interference: a) thermal or quantum fluctuations b) shot noise Mean amplitude of interference contains information on two-particle correlation functions. Higher moments contain additional information. Interference is a powerful tool for studying correlated cold atom systems.