Interference AH Physics QW Mr Stewart Interference of

Interference AH Physics Q&W Mr Stewart

Interference of waves �Wave interference can be observed in a number of ways. �We have already seen the production of stationary waves when a wave is reflected from a flat surface. �The superposition of the incident wave and the reflected wave produce an interference pattern of observable nodes and antinodes. A guitar string is a good example of a stationary wave. When plucked it vibrates at its fundamental frequency. If the string is touched at various positions it can be forced to produce “harmonics” of the fundamental frequency: 2 f, 3 f etc.

2 More examples of interference At AH Physics we study 2 other methods of producing an interference pattern with light waves. These are called: Division of amplitude. This is based on the principles of reflection and refraction. Division of wavefront. This is based on the principle of diffraction (You met this at Higher)

Division of Amplitude �When a light wave hits a transparent medium (ie glass) some of the light is reflected and some of the light is transmitted through the medium (refracted) �This means that the amplitude of the wave is divided. Some of the energy is reflected and some transmitted through. �This division of amplitude can cause interference patterns as a result of 2 reflections at different surfaces.

Division of Amplitude �A spectrum is often seen if petrol or oil is spilled on the ground. This is because there is reflection from the top and bottom surface of the thin film of oil. �Different colours are produced depending on the thickness of the thin film. Some reflected waves interfere constructively and some destructively. To gain a fuller understanding of this we need to introduce the idea of optical path difference

Optical path difference �When light passes from air into glass it slows down and the wavelength decreases. More wavelengths are contained within the same length l as shown in the above diagram. This “squeezing of the wavelength depends on the refractive index of the material. The optical length in a material is defined as: (Where n is the refractive index and d is the length of the more dense medium)

Thin film interference occurs when light reflects from the top and bottom surfaces of a thin film of a substance ie a soap bubble, petrol on a wet road etc. Ray 2 travels a greater distance than ray 1. The optical path difference between the rays = nd = 2 nt (where t is the thickness of the film) If the optical path difference is equal to half a wavelength, or then destructive interference will occur and that wavelength will not be seen in the reflected light. Note on the relationship sheet d is used for the minimum thickness of the film

Example……. A soap film on a car windscreen has a refractive index of 1. 35. The thickness of the film is such that green light of wavelength 550 nm is not reflected due to destructive interference by the thin film. a) Calculate the minimum thickness of the soap film. b) Explain why the windscreen has a purple colour a) b) Red and violet light are reflected, these mix to produce a purple colour

A note on thin film interference…. . Soap films and oil spillages produce random interference patterns due to irregular thicknesses of the film. Some expensive camera lenses have a thin coating deliberately placed on them to produce destructive interference for a particular wavelength. (usually green light in the middle of the visible spectrum) This “lens blooming” is called an anti-reflective coating and is designed to produce maximum transmission of the light into the camera. d = minimum thickness of coating n = refractive index of coating λ = wavelength of non-reflected light

Division of Amplitude experiment �An interference pattern can be produced by division of amplitude of monochromatic light using a set-up called “The Air Wedge” �This can be used to measure thickness of very thin materials Interference pattern seen when viewed from above.

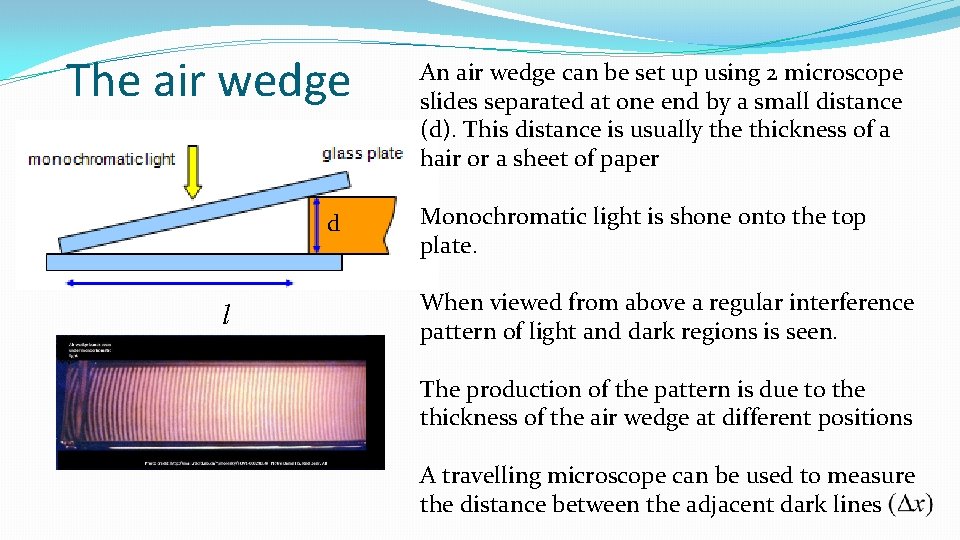
The air wedge d l An air wedge can be set up using 2 microscope slides separated at one end by a small distance (d). This distance is usually the thickness of a hair or a sheet of paper Monochromatic light is shone onto the top plate. When viewed from above a regular interference pattern of light and dark regions is seen. The production of the pattern is due to the thickness of the air wedge at different positions A travelling microscope can be used to measure the distance between the adjacent dark lines

A note on phase change on reflection �Light waves experience a phase change of π radians on reflection when they reflect from a more dense material ie air glass. �If the light is in glass and hits a glass air boundary there is no phase change on reflection. �This means there is no phase change at the bottom surface of the top slide but there is a phase change of π radians at the top surface of the bottom slide �Hence when the path difference is a whole number of λ, destructive interference is observed. �Constructive interference is observed when the path difference is an odd number of half wavelengths ie

Air wedge theory Light reflects from the bottom surface of the top slide and also from the top surface of the bottom slide. These 2 reflected rays have a path difference between them equal to twice thickness of the air wedge at a particular point. path difference = 2 t. (n=1 for air) If the path difference is a whole number of wavelengths then destructive interference occurs. (this is because there is a phase change on reflection only when the light hits the bottom slide) The next dark fringe will be seen at a position Δx when the path difference 2 t has increased by λ d

example A student places a thin copper wire between two microscope slides, This creates an air wedge as shown in the diagram below. A sodium lamp of wavelength 589 nm is incident on the apparatus from above. When viewed from above a series of light and dark “fringes” are seen. The student uses a travelling microscope and measure 10 fringe spacings. This is recorded as 4. 40 mm a) Calculate the diameter of the copper wire b) State why was 10 fringe spacings chosen and not just one. c) What effect, if any, would there be on the fringe spacing if a thicker wire replaced the original wire. Justify your answer 4 1 2 a) 0. 08 mm b) Reduce uncertainty in value of d. c) Δx smaller (relate to equation)

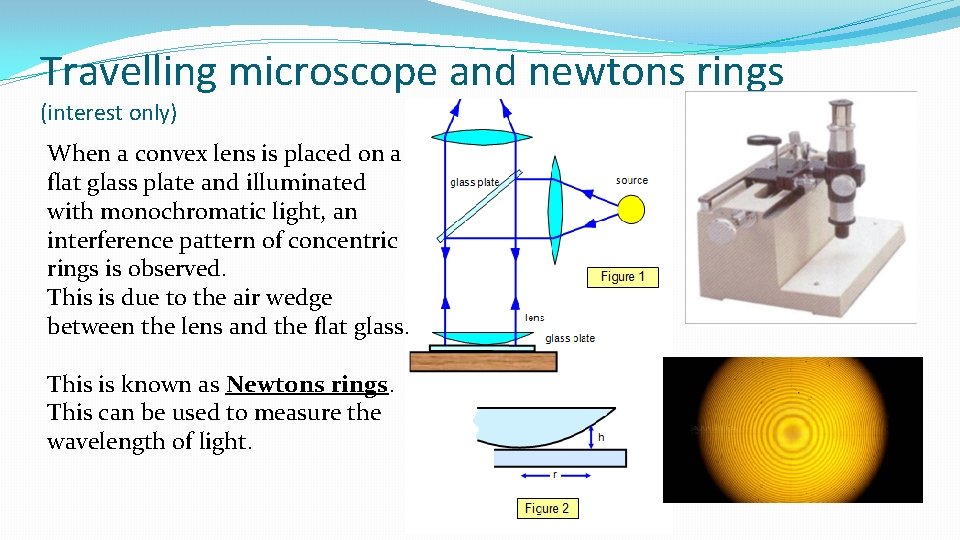
Travelling microscope and newtons rings (interest only) When a convex lens is placed on a flat glass plate and illuminated with monochromatic light, an interference pattern of concentric rings is observed. This is due to the air wedge between the lens and the flat glass. This is known as Newtons rings. This can be used to measure the wavelength of light.

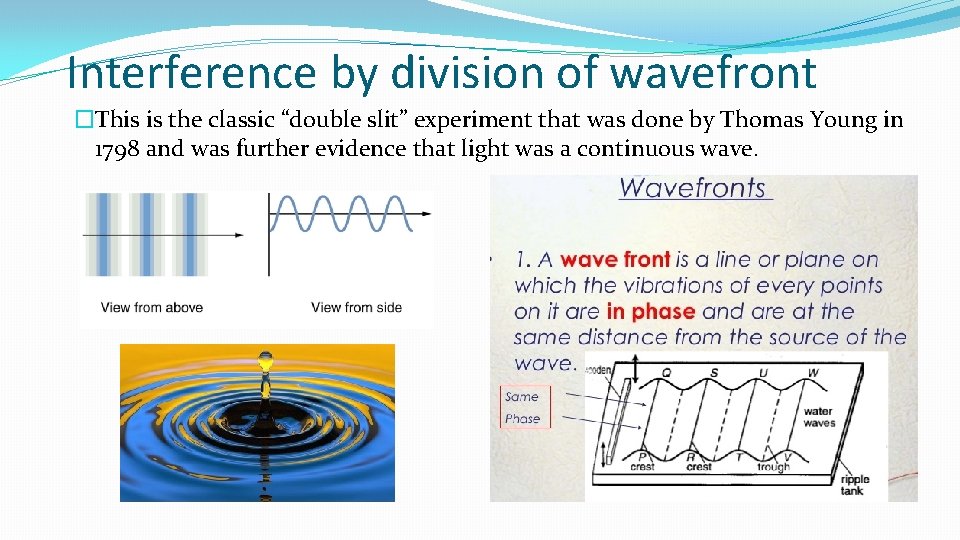
Interference by division of wavefront �This is the classic “double slit” experiment that was done by Thomas Young in 1798 and was further evidence that light was a continuous wave.

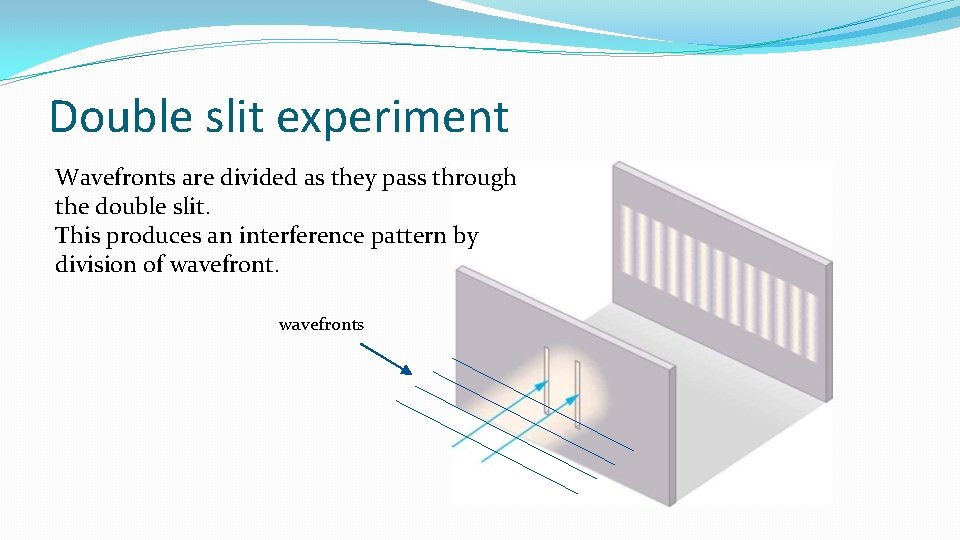
Double slit experiment Wavefronts are divided as they pass through the double slit. This produces an interference pattern by division of wavefronts

The double slit experiment revisited Wavefronts from a single monochromatic light source pass through a double slit. This produces (by diffraction) two coherent sets of semi-circular waves. These interfere and produce a pattern of light and dark fringes on a screen From the circled triangle: The path difference between the paths from slit 1 and slit 2 to the 1 st bright region is given by: λ is the wavelength of the light d is the slit separation Using the geometry of similar triangles: Δx = fringe separation D = distance to screen (This is called the small angle approximation)

Example: 2017 paper a) 657 nm b) unc in Δx = 3. 8% unc in d = 2. 4% unc in D = 0. 1% 4. 5% of 657 = 30 nm

A couple of points to note: For light of a constant wavelength (λ): �If the slit separation (d) is decreased, the fringe spacing (Δx) is increased �If the distance to the screen (D) is increased, the fringe spacing (Δx) is increased For a constant slit separation: �If wavelength is increased, the fringe spacing is increased. �(Δx is greater for red light is than for blue light)