Interest Rate Futures Chapter 6 Options Futures and

Interest Rate Futures Chapter 6 Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 1

Day Count Conventions in the U. S. (Page 129) Treasury Bonds: Actual/Actual (in period) Corporate Bonds: 30/360 Money Market Instruments: Actual/360 Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 2

Treasury Bond Price Quotes in the U. S Cash price = Quoted price + Accrued Interest Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 3

Treasury Bond Futures Pages 132 136 Cash price received by party with short position = Most recent settlement price × Conversion factor + Accrued interest Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 4

Example Most recent settlement price = 90. 00 Conversion factor of bond delivered = 1. 3800 Accrued interest on bond =3. 00 Price received for bond is 1. 3800× 90. 00+3. 00 = $127. 20 per $100 of principal Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 5

Interest Rate Futures Refinements In this chapter, we extend the discussion of interest rates futures. This chapter is organized into the following sections: 1. The T Bond Futures Contract 2. Seller’s Options for T Bond Futures 3. Interest Rate Futures Market Efficiency 4. Hedging with T Bond Futures Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 6

T Bond Futures Contract In this section, the discussion of T bond futures is extended by analyzing the cheapest to deliver bond. Recall that a number of candidate bonds can be delivered against a T bond future contract. Recall further that short traders choose when to deliver and which combination of bonds to deliver. Some bonds are cheaper to obtain than others. In this section, we learn techniques to identify the cheapest to deliver bond Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 7

Cheapest to Deliver with No Intervening Coupons Assume today, September 14, 2004, a trader observes that the SEP 04 T bond futures settlement price is 107 16 and thus decides to deliver immediately. That is, the trader selects today, September 14, as her Position Day. Therefore, she will have to deliver on September 16. The trader with the short position on futures is considering the following bonds with $100, 000 face value each for delivery. The short wishes to determine if delivering one or the other bond will produce a larger profit for her. How much should the trader receive? Which bond should the trader deliver? To answer these two questions, we need to determine the invoice amount and then which bond is cheapest to deliver. Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 8

Cheapest to Deliver with No Intervening Coupons Recall that the total price of a bond depends upon the quoted price plus the accrued interest (AI). Where: DSP = decimal settlement price the decimal equivalent of the quoted price CF = conversion factor the conversion factor as provided by the CBOT AI = accrued interest the Interest that has accrued since the last coupon payment on the bond Pi = cash market price Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 9

Cheapest to Deliver with No Intervening Coupons The accrued interest (AI) is computed as follows: The days in half year can be obtained from Table 8. 1. Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 10

Cheapest to Deliver with No Intervening Coupons Step 1: compute the cash price and invoice price. 5. 25% Bond AI = (122/184) (0. 5) (0. 0525) ($100, 000) = $1, 740. 49 Invoice Amount= 1. 0750 ($100, 000) (0. 9052) + $1, 740. 49 Invoice Amount = $99, 049. 49 8. 00% Bond AI = (122/184) (0. 5) (0. 08) ($100, 000) = $2, 652. 17 Invoice Amount= 1. 0750 ($100, 000) (1. 2113) + $2, 652. 17 Invoice Amount = $132, 866. 92 The 8% bond has an invoice amount 34% greater than the 5. 25% bond. Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 11

Cheapest to Deliver with No Intervening Coupons Sept 2: compute the cheapest-to-deliver bond. The bond that is most profitable to deliver is the cheapest to deliver bond. The trader’s profit is the difference between the invoice amount and the cash market price. For a particular bond I, the profit πi is: πi = Invoice Amount (Pi + AIi) Recall that the invoice amount is: Substituting the formula for the invoice amount into the profit equation gives: πi = (DFPi) ($100, 000) (CFi) + AIi (Pi + AIi) And simplifying: πi = DFPi ($100, 000) (CFi) Pi Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 12

Cheapest to Deliver with No Intervening Coupons The cheapest to deliver is: 5. 25% Bond π = 1. 0750 ($100, 000) (0. 9052) $93, 468. 75 = $3, 840. 25 8. 00% Bond π = 1. 0750 ($100, 000) (1. 2113) $127, 093. 75 = $3, 121. 00 Thus, in this case the cheapest to deliver bond is the 5. 25% bond. Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 13

Cheapest to Deliver with No Intervening Coupons General rules based on interest rates: 1. When interest rates are below 6%, there is an incentive to deliver short maturity/high coupon bonds. 2. When interest rates exceed 6%, there is an incentive to deliver long maturity/low coupon bonds. General rules based on duration: 1. A trader should deliver low duration bonds when interest rates are below 6%. 2. A trader should deliver high duration bonds when interest rates are above 6%. Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 14

Cheapest to Deliver with Intervening Coupons This section examines, cheapest to deliver bonds when a bond pays a coupon between the beginning of the cash and carry holding period and the futures expiration. To find the cheapest to deliver bond before expiration, the cash and carry strategy is used. The bond with the greatest profit at delivery from following the cash and carry strategy will be the cheapest to deliver bond. For this analysis Assume that: 1. A trader buys a bond a today and carries it until delivery. 2. Interest rates and futures prices remain constant. 3. Consider the estimated invoice amount plus the estimate of the cash flows associated with carrying the bond to delivery. Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 15

Cheapest to Deliver with Intervening Coupons The estimated invoice amount depends on three factors: 1. Today's quoted futures price. 2. The conversion factor for the bond we plan to deliver. 3. The accrued interest on the bond at the expiration date. Acquiring and carrying a bond to delivery involves three cash flows as well: 1. The amount paid today to purchase the bond. 2. The finance cost associated with obtaining money today to buy a bond in the future. 3. The receipt and reinvesting of coupon payment. Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 16

Cheapest to Deliver with Intervening Coupons Estimated Invoice Amount = DFP 0 $100, 000 (CF) + AI 2 Estimated Future Value of the Delivered Bond = (P 0 + AI 0)(1 + C 0, 2) COUP 1(1 + C 1, 2) For bond I, the expected profit from delivery is the estimated invoice amount minus the estimated value of what will be delivered: π = DFP 0 ($100, 000) (CF) + AI 2 {(P 0 + AI 0)(1 + C 0, 2) COUP 1(1 + C 1, 2)} where: P 0 = quoted price of the bond today, t = 0 AI 0 = accrued interest as of today, t = 0 C 0, 2 = interest factor for t = 0 to expiration at t = 2 COUP 1 = coupon to be received before delivery at t = 1 C 1, 2 = interest factor from t = 1 to t = 2 DFP 0 = decimal futures price today, t = 0 CF = conversion factor for a particular bond and the specified futures expiration Options, Futures, and Other Derivatives, AI 2 = accrued interest at t = 2 7 th Edition, Copyright © John C. Hull 2008 17

Cheapest to Deliver with Intervening Coupons To illustrate these computation consider the following situation. Suppose that today is Sept 14, 2004, and you want to find the cheapest to deliver bond for the DEC 04 futures expiration. The bond has a $100, 000 face value and a target delivery date of Dec 31, 2004. The futures contract is the DEC 04. The T bond contract had a settlement price of 106 23 today. The coupon invested repo rates is 7%. Summary Today = Bond face value = Target delivery date = Futures contract = Coupon invested repo rate = Settlement price Sept 14 = You Sept 14 $100, 000 Dec 31 DEC 04 T bond 7% 106 23 are considering two bonds for delivery. The bonds are as follows: Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 18

Cheapest to Deliver with Intervening Coupons Step 1: estimate the value of AI. 5. 25% Bond P 0 + AI 0 = $93, 468. 75 + $1, 740. 49 = $95, 209. 24 8% Bond P 0 + AI 0 = $ 127, 093. 75 + $2, 652. 17 = $129, 745. 92 Step 2: estimate the accrued interest that will accumulate from the next coupon date, Nov 15, 2004 if the planned delivery date is Dec 31, 2004 (46 days). 5. 25% Bond AI 2 = (46/181) (0. 5) (0. 0525) ($100, 000) = $667. 13 8% Bond AI 2 = (46/181) (0. 5) (0. 08) ($100, 000) = $1, 016. 57 Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 19

Cheapest to Deliver with Intervening Coupons Step 3: compute the estimated invoice amounts. 5. 25% Bond 1. 0671875 ($100, 000) (0. 9056) + $667. 13 = $97, 311. 63 8% Bond 1. 0671875 ($100, 000) (1. 2094) + $1, 016. 57 = $130, 082. 23 Step 4: compute financing rates. Period: Sept 15 until Dec 31 (108 days) C 0, 2 = 0. 07 (108/360) = 0. 0210 Period: Nov 15 until Dec 31 (46 days) C 1, 2 = 0. 07 (46/360) = 0. 008944 Table 8. 2 summarizes these calculations. Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 20

Cheapest to Deliver with Intervening Coupons Step 5: Compute expected profit for each bond. 5. 25% Bond π = (1. 06718750) ($100, 000) (0. 9056) + $667. 13 [($ 93, 468. 75 + $1, 740. 49) ( 1. 0210 ) ($2, 625) ( 1. 008944 )] π = $2, 751. 48 8% Bond π= (1. 06718750) ($100, 000) (1. 2094) + $1, 016. 57 [($127, 093. 75 + $2, 652. 17) (1. 0210) $4, 000 (1. 008944)] π =$1, 647. 43 The profit from the 5. 25% bond is higher, so it is the cheapest to deliver. Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 21

Conversion Factor The conversion factor for a bond is approximately equal to the value of the bond on the assumption that the yield curve is flat at 6% with semiannual compounding Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 22

CBOT T Bonds & T Notes Factors that affect the futures price: ◦ Delivery can be made any time during the delivery month ◦ Any of a range of eligible bonds can be delivered ◦ The wild card play Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 23

Wildcard Option The settlement price is determined at 2: 00 PM. However, the short seller has until 8: 00 PM to notify the exchange of his/her intent to deliver. Thus, the seller can observe what happens between 2: 00 PM and 8: 00 PM before making his/her decision. If interest rates jump between 2: 00 PM and 8: 00 PM, the short trader notifies the exchange his/her intent to deliver at the 2: 00 PM price. If interest rates stay the same or go down, the short seller waits for the next day to notify the exchange of an intent to deliver. Chapter 8 24

Eurodollar Futures (Page 136 141) A Eurodollar is a dollar deposited in a bank outside the United States Eurodollar futures are futures on the 3 month Eurodollar deposit rate (same as 3 month LIBOR rate) One contract is on the rate earned on $1 million A change of one basis point or 0. 01 in a Eurodollar futures quote corresponds to a contract price change of $25 Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 25

Eurodollar Futures continued A Eurodollar futures contract is settled in cash When it expires (on the third Wednesday of the delivery month) the final settlement price is 100 minus the actual three month deposit rate Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 26

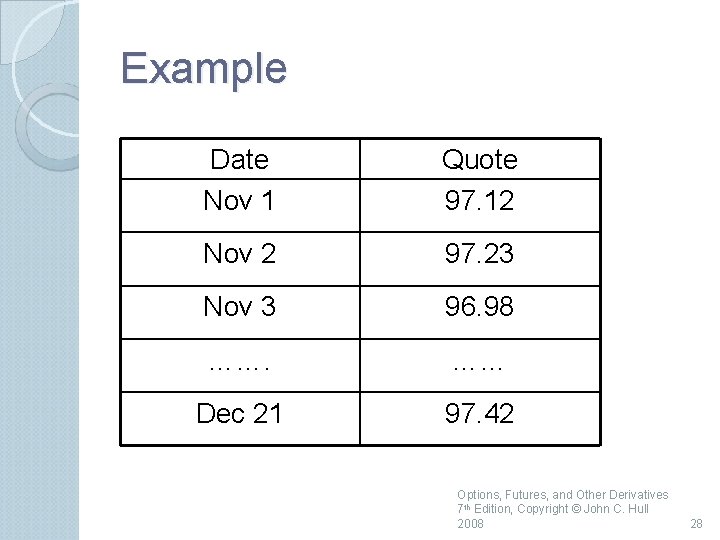
Example Suppose you buy (take a long position in) a contract on November 1 The contract expires on December 21 The prices are as shown How much do you gain or lose a) on the first day, b) on the second day, c) over the whole time until expiration? Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 27

Example Date Nov 1 Quote 97. 12 Nov 2 97. 23 Nov 3 96. 98 ……. …… Dec 21 97. 42 Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 28

Example continued If on Nov. 1 you know that you will have $1 million to invest on for three months on Dec 21, the contract locks in a rate of 100 97. 12 = 2. 88% In the example you earn 100 – 97. 42 = 2. 58% on $1 million for three months (=$6, 450) and make a gain day by day on the futures contract of 30×$25 =$750 Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 29

Formula for Contract Value (page 138) If Q is the quoted price of a Eurodollar futures contract, the value of one contract is 10, 000[100 0. 25(100 Q)] Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 30

Forward Rates and Eurodollar Futures (Page 139 142) Eurodollar futures contracts last as long as 10 years For Eurodollar futures lasting beyond two years we cannot assume that the forward rate equals the futures rate Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 31

There are Two Reasons Futures is settled daily where forward is settled once Futures is settled at the beginning of the underlying three month period; FRA is settled at the end of the underlying three month period Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 32

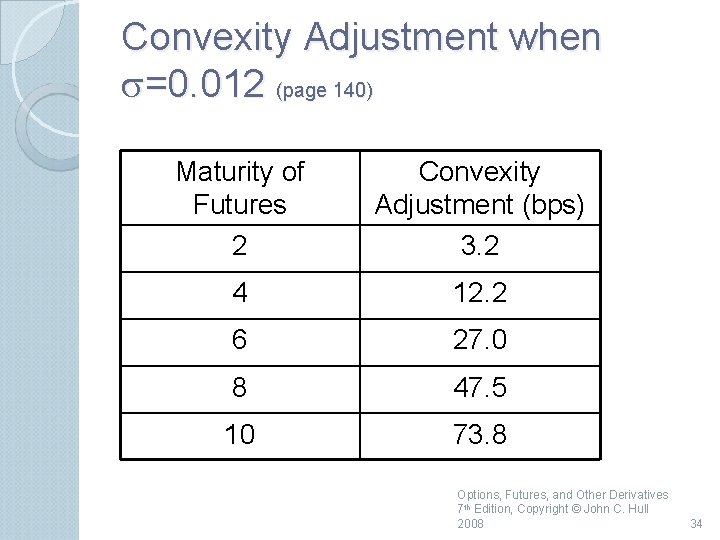
Forward Rates and Eurodollar Futures continued A convexity adjustment often made is Forward Rate=Futures Rate− 0. 5 s 2 T 1 T 2 T 1 is the time to maturity of the forward contract T 2 is the time to maturity of the rate underlying the forward contract (90 days later that T 1) s is the standard deviation of the short rate (typically about 1. 2%) Options, Futures, and Other Derivatives, 7 th Edition, Copyright © John C. Hull 2008 33

Convexity Adjustment when s=0. 012 (page 140) Maturity of Futures 2 Convexity Adjustment (bps) 3. 2 4 12. 2 6 27. 0 8 47. 5 10 73. 8 Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 34

Extending the LIBOR Zero Curve LIBOR deposit rates define the LIBOR zero curve out to one year Eurodollar futures can be used to determine forward rates and the forward rates can then be used to bootstrap the zero curve Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 35

Example (page 141 142) so that If the 400 day LIBOR rate has been calculated as 4. 80% and the forward rate for the period between 400 and 491 days is 5. 30 the 491 day rate is 4. 893% Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 36

Duration Matching This involves hedging against interest rate risk by matching the durations of assets and liabilities It provides protection against small parallel shifts in the zero curve Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 37

Use of Eurodollar Futures One contract locks in an interest rate on $1 million for a future 3 month period How many contracts are necessary to lock in an interest rate on $1 million for a future six month period? Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 38

Duration Based Hedge Ratio FC Contract price for interest rate futures DF Duration of asset underlying futures at maturity P Value of portfolio being hedged DP Duration of portfolio at hedge maturity Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 39

Example It is August. A fund manager has $10 million invested in a portfolio of government bonds with a duration of 6. 80 years and wants to hedge against interest rate moves between August and December The manager decides to use December T bond futures. The futures price is 93 02 or 93. 0625 and the duration of the cheapest to deliver bond is 9. 2 years The number of contracts that should be shorted is Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 40

Limitations of Duration Based Hedging Assumes that only parallel shift in yield curve take place Assumes that yield curve changes are small When T Bond futures is used assumes there will be no change in the cheapest to deliver bond Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 41

GAP Management (Business Snapshot 6. 3) This is a more sophisticated approach used by banks to hedge interest rate. It involves ◦ Bucketing the zero curve ◦ Hedging exposure to situation where rates corresponding to one bucket change and all other rates stay the same Options, Futures, and Other Derivatives 7 th Edition, Copyright © John C. Hull 2008 42