Interconnection Networks o Lecture 5 January 29 th

Interconnection Networks o Lecture 5 : January 29 th 2007 Prof. Chung-Kuan Cheng University of California San Diego Transcribed by: Jason Thurkettle

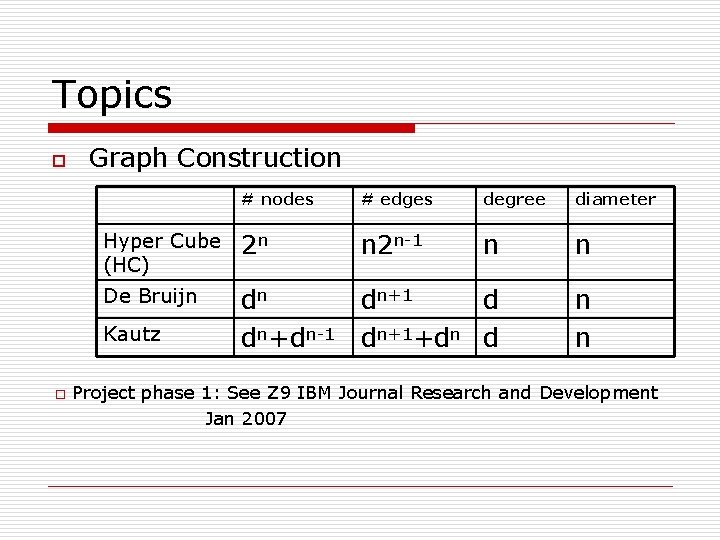
Topics o Graph Construction # nodes # edges degree diameter Hyper Cube (HC) 2 n n 2 n-1 n n De Bruijn dn dn+1 d dn+dn-1 dn+1+dn d n n Kautz o Project phase 1: See Z 9 IBM Journal Research and Development Jan 2007

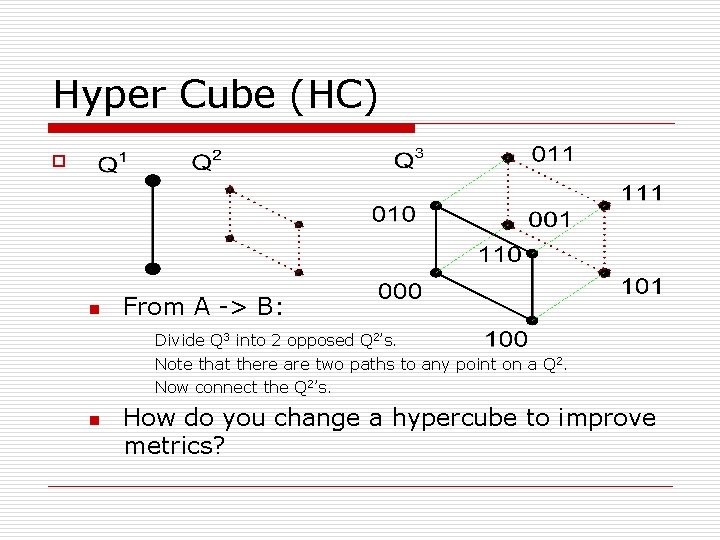
Hyper Cube (HC) o n From A -> B: Divide Q 3 into 2 opposed Q 2’s. Note that there are two paths to any point on a Q 2. Now connect the Q 2’s. n How do you change a hypercube to improve metrics?

Hypercube Variations n n n Generalized Hypercube Toroidal Mesh Hypercube Crossed Hypercube Folded Hypercube Connected Hypercube

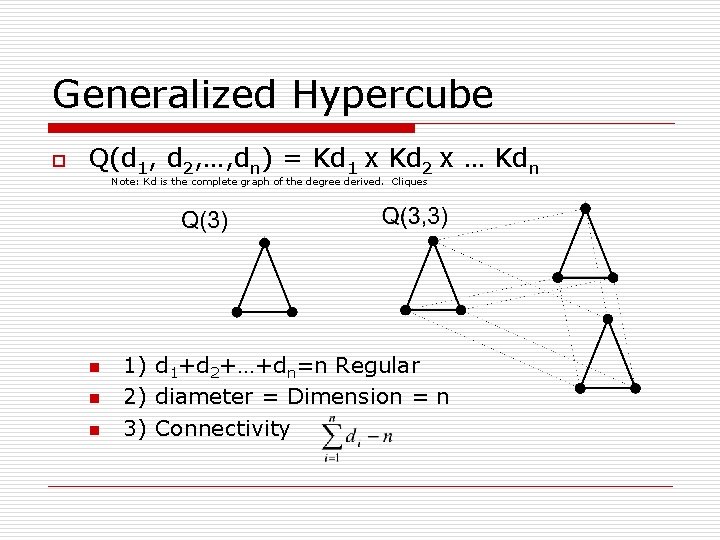
Generalized Hypercube o Q(d 1, d 2, …, dn) = Kd 1 x Kd 2 x … Kdn Note: Kd is the complete graph of the degree derived. Cliques n n n 1) d 1+d 2+…+dn=n Regular 2) diameter = Dimension = n 3) Connectivity

Toroidal Mesh Hypercube C(d 1, d 2, …, dn) o n x = x 1, x 2, …, xn & y = y 1, y 2, …, yn : are linked iff or C(d 1, d 2, …, dn) = Cd 1 x. Cd 2 x…x. Cdn where Cdi is a undirected cycle n n 1) 2) 3) 4) 2 n regular diameter = connectivity = 2 n # nodes =

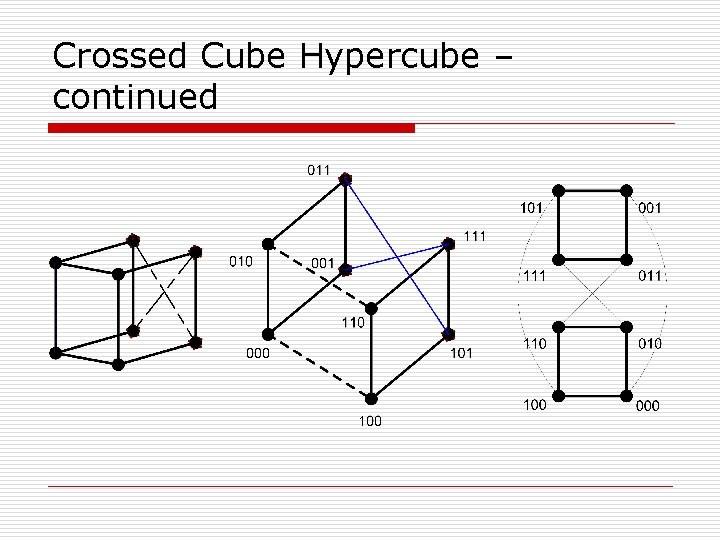
Crossed Cube Hypercube CQ(V, E) o n x = x 1, x 2, …, xn & y = y 1, y 2, …, yn : are linked iff o a) xn…xj+1 = yn…yj+1 o b) xj ≠ yj o c) xj-1 = yj-1 if j is even o d) x 2 i, x 2 i-1 ~ y 2 i, y 2 i-1 e. g. x 1 x 2 ~ y 1 y 2 : {(00, 00), (10, 10), (01, 11), (11, 01)} o o o 1) 2 n vertices, n 2 n-1 edges 2) diameter 3) connectivity n

Crossed Cube Hypercube – continued

Folded Hypercube FQ(V, E) Start with a Hypercube Qn: Add edges (x, y) if i. e. linking the longest distance pairs n n 1) 2) 3) 4) 2 n vertices (n+1)2 n-1 edges n+1 regular diameter connectivity n+1

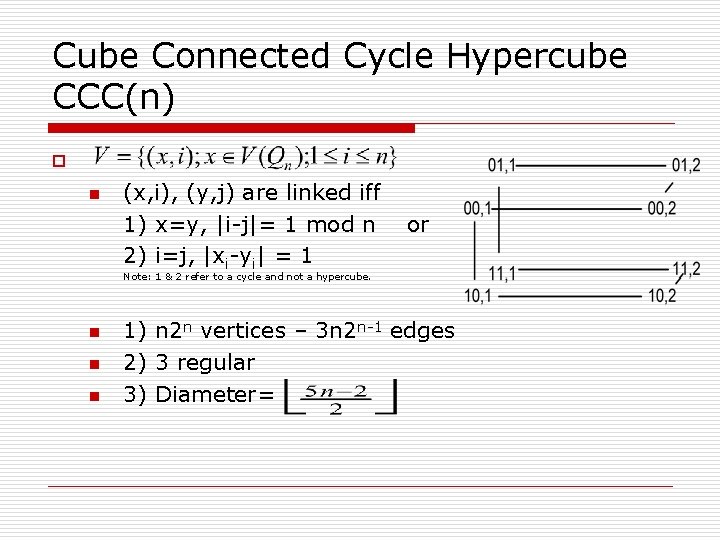
Cube Connected Cycle Hypercube CCC(n) o n (x, i), (y, j) are linked iff 1) x=y, |i-j|= 1 mod n 2) i=j, |xi-yi| = 1 or Note: 1 & 2 refer to a cycle and not a hypercube. n n n 1) n 2 n vertices – 3 n 2 n-1 edges 2) 3 regular 3) Diameter=

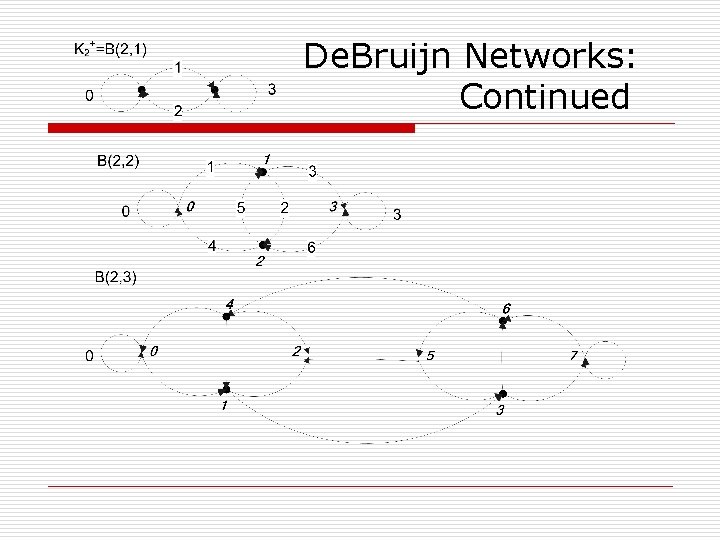
De Bruijn Network 1946 B(d, n) o Def 1: d-ary sequence of length n n o Def 2: iterated line digraphs n B(d, 1) = Kd+ B(d, n)=Ln-1 (Kd+) Note: Kd+ is a complete d vertex graph o Def 3: V = {0, 1, …, dn-1} n≥ 2 E={(x, y), y=xd+β mod dn, β=0, 1, …d-1} n n n 1) dn vertices, dn+1 edges 2) d regular 3) diameter = n

De. Bruijn Networks: Continued