Interactive Proof Systems Def Graph Isomorphism Given 2

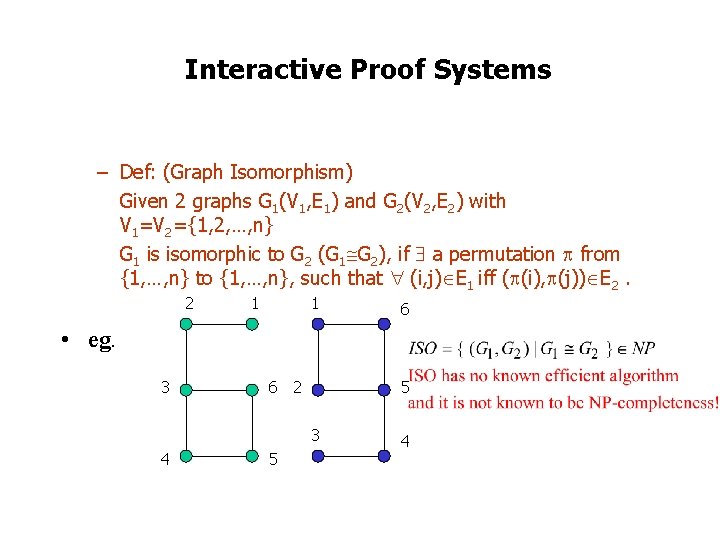
Interactive Proof Systems – Def: (Graph Isomorphism) Given 2 graphs G 1(V 1, E 1) and G 2(V 2, E 2) with V 1=V 2={1, 2, …, n} G 1 is isomorphic to G 2 (G 1 G 2), if a permutation from {1, …, n} to {1, …, n}, such that (i, j) E 1 iff ( (i), (j)) E 2. 2 1 1 6 • eg. 3 6 2 5 3 4 5 4

– Def: (Graph non-isomorphism) NONISO={ (G 0, G 1) | G 0 and G 1 are not isomorphic}. • Arthur Merlin game: king wizard with supernatural abilities – Def: A set L has an Arthur-Merlin proof system if an interactive TM A (Arthur) s. t. : • 1) Exists an interactive TM M (Merlin) s. t. for x L , Pr[A accepts x ] 2/3. • 2) For all possible interactive TM M s. t. the pair (M, A) form an interactive protocol, and for x L, Pr[A accepts x]<1/3.

• eg. NONISO={ (G 0, G 1)|G 0≇G 1 }. |V|=n. INPUT: G 0 and G 1. 1. Mv reads the input an randomly selects n integers ci {0, 1} (toss coins). For each ci, 1 i n, Mv computes a graph Hi which is isomorphic to. At the end, Mv sends to Mp : H 1, H 2, …, Hn.

2. The prover reads the input and tests if G 0 is isomorphic for to G 1. • If G 0 is not isomorphic to G 1, then Mp reads the message sent by the verifier. For each Hi, Mp tests whether Hi G 0 or Hi G 1. • If G 0 G 1 then for each i, Mp can only guess with probability ½. • Mp sends the answers to Mv. 3. Mv compare the answers, for i=1, …, n. If it is incorrect for some i, then it means that either the graphs are isomorphic, or the prover made a mistake, and Mv rejects. Otherwise, Mv verifies G 0 ≇ G 1.

• Interactive Proof Systems provide a way to define a probabilistic analog to NP, that is BPNP. • The language in P are those whose members all have short certificates (evidence) of membership that can be verified efficiently. • Rephrase the above by two entities: Prover (powerful) finds the proof of membership. Verifier checks the correctness of proof in poly time. Prover tries to convince Verifier of w’s membership in A. 1. Two-way communication between Prover and Verifier. 2. Verifier can be a probabilistic TM.

Formal definition of interactive proof system: 1. Verifier V: * * {accept, reject} V(w, r, m 1# m 2# … # mi)= mi+1 w: the input, r: the random string, m 1# m 2# … # mi: the current message history mi+1: Verifier’s next message to the Prover. 2. Prover P: * * * P(w, m 1# m 2# … # mi)= mi+1 means that the P sends mi+1 to V after exchanging m 1# m 2# … # mi

(V P)(w, r) = accept if a message sequence m 1# m 2# … # mk exists for some k and 1. For 0<= i < k, where i is an even number, V(w, r, m 1# m 2# … # mi)= mi+1; 2. For 0< i < k, where i is an odd number, P(w, m 1# m 2# … # mi)= mi+1; and 3. The final message mk in the message history is accept.

Define Pr[V P accepts w] = Pr[(V P)(w, r) = accept], where r is a randomly selected string of length p(|w|). Definition: A is in IP if some poly time function V and arbitrary function P exist, where for every function P’ and string w 1. w A implies Pr[V P accepts w] 2/3, and 2. w A implies Pr[V P’ accepts w] 1/3. The error probability can be reduced by amplification lemma. Goal: Prove IP = PSPACE.

Lemma: IP PSPACE. Proof: Let A IP. Assume A’s verifier V exchanges exactly p=p(|w|) messages. Construct a PSPACE TM M to simulate V. For any w define Pr[V accepts w] = max_P Pr[[V P accepts w], which we show to calculate in poly time.

Let Mj denote m 1# m 2# … # mj. Write (V P)(w, r, Mj)=accept if we can extend Mj with messages mj+1 through mp so that 1. For j<= i < p, where i is an even number, V(w, r, Mi)= mi+1; 2. For j<= i < p, where i is an odd number, P(w, Mi)= mi+1; and 3. The final message mp in the message history is accept.

Define Pr[V P accepts w starting at Mj] = Pr[(V P)(w, r, Mj) = accept], where r is a randomly selected string of length p(|w|). Define Pr[V accepts w starting at Mj] = max_P Pr[V P accepts w starting at Mj]. For every 0<=j <= p and every message stream Mj define

Let M 0 be the empty message stream. NM 0 can be computed in poly space, since it is computed by recursion and the depth of recursion is p. Goal: NM 0 =Pr[V accepts w]. Claim For every 0<= j <= p and every Mj, NMj = Pr[V accepts w starting at Mj]. Prove by induction on j, where the basis is j=p and the induction proceeds from p down to 0. Basis: For j=p, we have mp is either accept or reject. If mp is accept then NMp =1 and Pr[V accepts w starting at Mj] =1. Similarly for mp =reject.

Induction step: Assume it is true for some j+1 <=p and any message stream Mj+1. Want to prove that it is true for j and any message stream Mj. If j is even, mj+1 is a message from V to P: If j is odd, mj+1 is a message from P to V: QED.

Define counting problem for SAT: #SAT={< , k>| is cnf-formula with exactly k satisfying assignments}. Theorem: #SAT IP. Proof: has exactly k satisfying assignments iff there exists k 0, k 1 such that 1. k 0 + k 1= k 2. 0(x 1, x 2, …, xn) = (0, x 2, …, xn) has exactly k 0 satisfying assignments. 3. 1(x 1, x 2, …, xn) = (1, x 2, …, xn) has exactly k 1 satisfying assignments.

and k are given to both P and V. Arithmetization: We’ll extend : {0, 1}n {0, 1} to p: Fn F, where F is a large finite field, so p is a low-degree polynomial. 1. (x 1, …, xn) =p(x 1, …, xn), if for all xi {0, 1}. 2. d = degree (p) | | 3. p(x) can be evaluated in poly time given and x Fn The transform is done recursively by: 1 -(1 - )

Choose F=Zq, where q is a prime such that q> 2 d > 2 n. P wants to prove to V that: x 1 {0, 1} x 2 {0, 1}………. xn {0, 1}p(x 1, …, xn)=k. The domain of is in F. (*) Let k = x 2 {0, 1}………. xn {0, 1}p( , x 2, …, xn) P: send {k } for all in F. ---- this can be a long list! V: 1. Check k 0 + k 1= k 2. Choose from F randomly 3. Send The protocol continues with the recursive proof on p( , x 2, …, xn) and k.

P: 1. Compute degree d polynomial p 1(x)= x 2 {0, 1}………. xn {0, 1}p(x, x 2, …, xn). 2. Send the coefficients of p 1 to V. V: 1. Check p 1(0)+ p 1(1) = k 2. Choose 1 F randomly and send it to P. P: 1. Compute polynomial p 2(x)= x 3 {0, 1}………. xn {0, 1}p( 1 , x, x 3, …, xn). 2. Send the coefficients of p 2 to V. V: 1. Check p 2(0)+ p 2(1) = p 1( 1 ) 2. Choose 2 F randomly and send it to P. ……….

Continue for n rounds…. V: 1. Check pn(0)+ pn(1) = pn-1( n-1 )? 2. Choose n F randomly 3. Check pn( n ) = p( 1, …, n)? 4. Accept if all of these checks pass, reject otherwise. Claim: The above is an interactive proof for #SAT. Pf: 1. V spends polynomial time, because of arithmetization. 2. Suppose does not have k satisfying assignments. We show that for all P*, Pr[ V P* accepts ( , k)] nd/|F| 0. Let p 1*, …. , pn* be the polynomials sent by P*. Let p 1, …. , pn be the polynomials computed according to specified P-strategy.

Assume p 1(0)+ p 1(1) = # satisfying assignments to k. Then either p 1*(0)+ p 1*(1) k or p 1* p 1. In the first case V rejects immediately. Otherwise, with probability > 1 - d/|F|, p 1* ( 1) p 1 ( 1). Suppose p 1* ( 1) p 1 ( 1)= p 2(0)+ p 2(1). Then either -- p 2*(0)+ p 2*(1) p 2* ( 1)---V rejects immediately. -- p 2* p 2 implies with probability > 1 - d/|F|, over 2 p 2* ( 2) p 2 ( 2). -- etc… By union bound, Pr[ V P* rejects or pn* ( n) pn ( n)] 1 -nd/|F| 2/3.

Lemma: PSPACE IP Proof: Goal: To show TQBF is in IP. Let =Q 1 x 1 Q 2 x 2. . Qmxm[ ], where is a cnf-formula and Qi is or . For all i in [m], ai {0, 1} let fi(a 1, . . . , ai) = 1 if Qi+1 xi+1. . Qmxm[ (a 1, . . . , ai)] is true, 0 otherwise. Qi+1 is : fi(a 1, . . . , ai) = fi+1(a 1, . . . , ai, 0) · fi+1(a 1, . . . , ai, 1) and Qi+1 is : fi(a 1, . . . , ai) = fi+1(a 1, . . . , ai, 0) *fi+1(a 1, . . . , ai, 1), x*y = 1 -(1 -x)(1 -y).

To arithmetize we introduce ’ = Qx 1 Rx 1 Qx 2 Rx 1 Rx 2 Qx 3 Rx 1 Rx 2 Rx 3. . . Qmxm Rx 1. . Rxm[ ]. Rewrite ’ = S 1 y 1 S 2 y 2. . . Skyk [ ], where Si { , , R} and yi {x 1, . . . , xm}. Define fk(x 1, . . . , xm) to be the poly p(x 1, . . . , xm) obtained by arithmetizing . For i<k we define fi in terms of fi+1: Si+1= : fi (. . . )= fi+1(. . . , 0)· fi+1(. . . , 1) Si+1= : fi (. . . )= fi+1(. . . , 0)* fi+1(. . . , 1) Si+1= R: fi (. . . , a)=(1 -a)fi+1(. . . , 0) + a fi+1(. . . , 1) If S is or , fi has one fewer input variable than fi+1. If S is R, the two functions have the same number of input variables.

Note that Rx operation on polynomial does not change their values on Boolean inputs and produces a result that is linear in x. Therefore f 0( ) is still the truth value of . Add Rx 1. . Rxi after Qixi in ’ in order to reduce the degree of each variable to 1 prior to the squaring due to arithmetizing Qi. Select a field F of size at least n 4, where n is the length of . Phase 0: P: sends f 0( ) to V V: Check that f 0( ) =1 and rejects if not.

Phase i: [P persuades V that fi-1(r 1. . . ) is correct if fi(r 1. . . , r) is correct. ] P: Sends the coefficients of fi(r 1. . . , z) as a poly in z. V: Evaluates fi(r 1. . . , 0) and fi(r 1. . . , 1). Checks that the poly degree is n and that the identities: fi-1(r 1. . . ) = fi(r 1. . . , 0). fi(r 1. . . , 1) if S= fi-1(r 1. . . ) = fi(r 1. . . , 0)*fi(r 1. . . , 1) if S= or fi-1(r 1. . . , r) = (1 -r) fi(r 1. . . , 0) + r fi(r 1. . . , 1) if S=R. If either fails, V rejects. Pick a random r in F and sends it to P. . . .

Phase k+1: [V checks fk(r 1, . . . , rm) is correct. ] V: Evaluates p(r 1, . . . , rm) to compare with the value V has for fk(r 1, . . . , rm). If the values are the same, then accepts. ; O/W rejects. The correctness of this protocol is similar to the proof for #SAT. If is true, P can follow the protocol and V will accept. If is false, P* must lie at phase 0 by sending an incorrect value for f 0(). At phase i, if V has an incorrect value for fi-1(r 1. . . ), one of the values fi(r 1. . . , 0) and fi(r 1. . . , 1) must be wrong and the poly for fi must be incorrect.

Consequently, for a random r the poly that P* gets lucky at this phase because fi(r 1. . . , z)|z=r is correct is n/n 4. The protocol proceeds for O(n 2) phases, so the probability that P* gets lucky at some phase is at most 1/n. If P* is never lucky, V will reject at phase k+1. QED.