Interaction Xrays Matter Pair production 1 M e



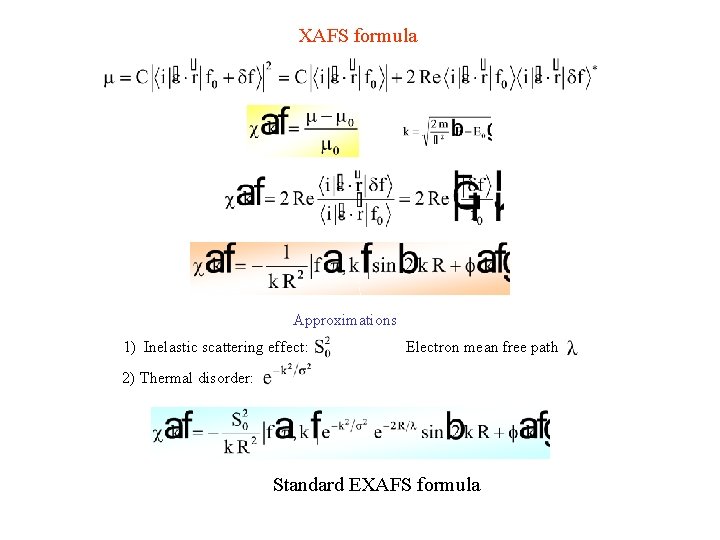
- Slides: 27

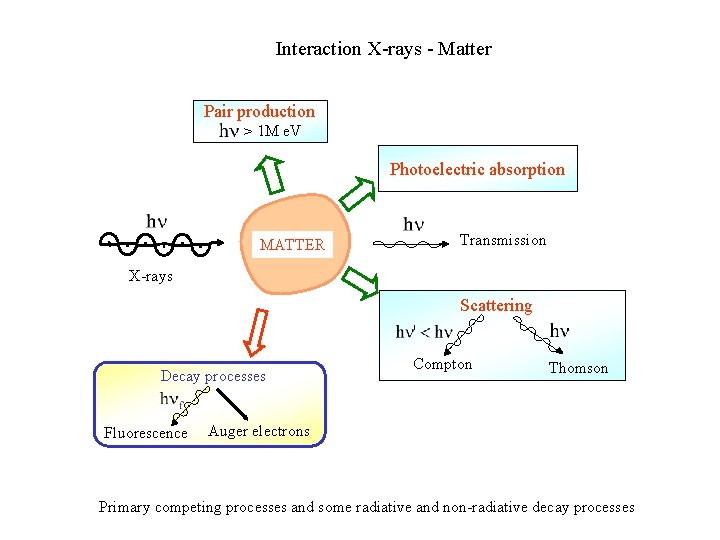
Interaction X-rays - Matter Pair production > 1 M e. V Photoelectric absorption MATTER Transmission X-rays Scattering Decay processes Fluorescence Compton Thomson Auger electrons Primary competing processes and some radiative and non-radiative decay processes

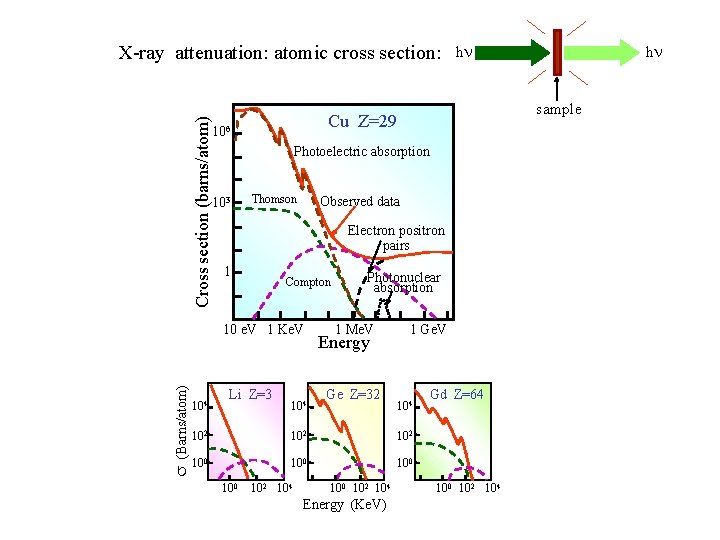
Cross section (barns/atom) X-ray attenuation: atomic cross section: Photoelectric absorption 103 Thomson Observed data Electron positron pairs 1 Compton s (Barns/atom) 10 e. V 1 Ke. V 104 sample Cu Z=29 106 Li Z=3 104 Photonuclear absorption 1 Me. V Energy Ge Z=32 1 Ge. V 104 102 102 100 100 102 104 Energy (Ke. V) h h Gd Z=64 100 102 104

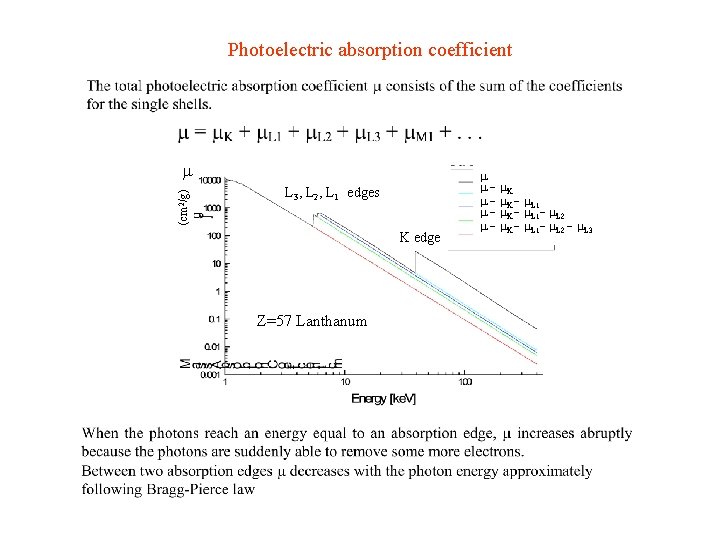
Photoelectric absorption coefficient (cm 2/g) L 3, L 2, L 1 edges K edge Z=57 Lanthanum - K - L 1 - L 2 - L 3

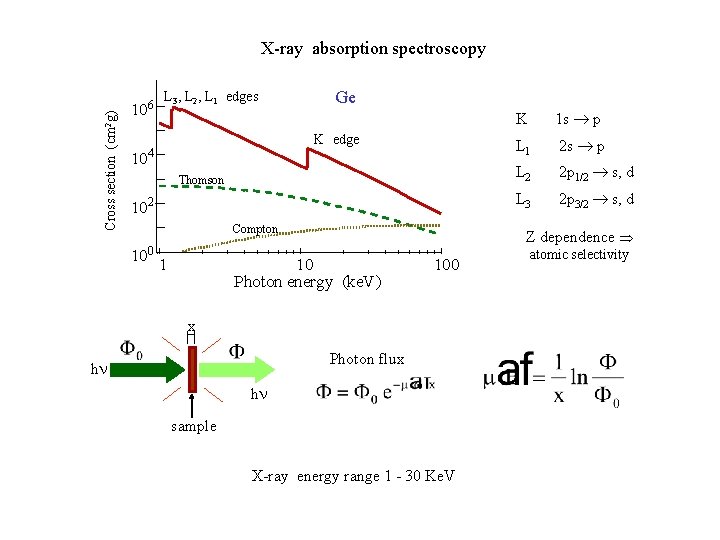
Cross section (cm 2 g) X-ray absorption spectroscopy 106 10 L 3, L 2, L 1 edges Ge K edge 4 Thomson 102 Compton 10 0 1 1 s ® p L 1 2 s ® p L 2 2 p 1/2 ® s, d L 3 2 p 3/2 ® s, d Z dependence Þ 10 Photon energy (ke. V) 100 x Photon flux h K h sample X-ray energy range 1 - 30 Ke. V atomic selectivity

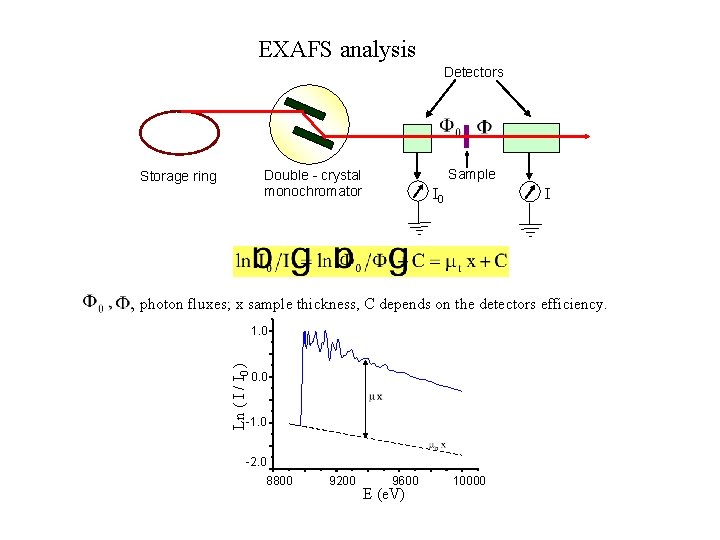
EXAFS analysis Detectors Sample Double - crystal monochromator Storage ring I 0 I photon fluxes; x sample thickness, C depends on the detectors efficiency. Ln ( I / I 0 ) 1. 0 0. 0 -1. 0 -2. 0 8800 9200 9600 E (e. V) 10000

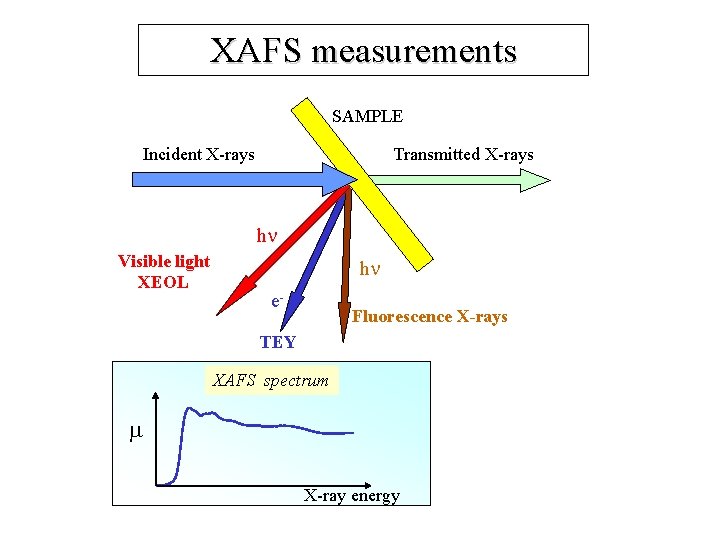
XAFS measurements SAMPLE Incident X-rays Transmitted X-rays h Visible light XEOL h e- Fluorescence X-rays TEY XAFS spectrum X-ray energy

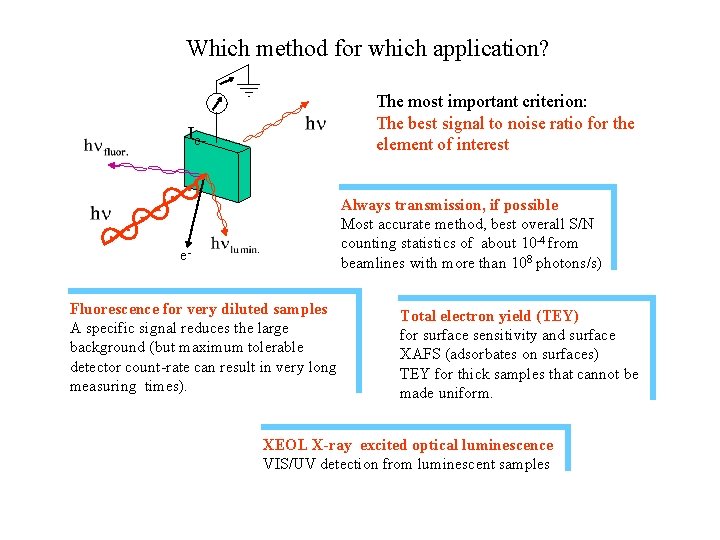
Which method for which application? The most important criterion: The best signal to noise ratio for the element of interest Ie- Always transmission, if possible Most accurate method, best overall S/N counting statistics of about 10 -4 from beamlines with more than 108 photons/s) e. Fluorescence for very diluted samples A specific signal reduces the large background (but maximum tolerable detector count-rate can result in very long measuring times). Total electron yield (TEY) for surface sensitivity and surface XAFS (adsorbates on surfaces) TEY for thick samples that cannot be made uniform. XEOL X-ray excited optical luminescence VIS/UV detection from luminescent samples

Measurement sensitivity in transmission mode Sample = Species (A + B) A = solute, B = Solvent By changing the solute absorption coefficient For x and Statistically: so that Assuming that the solute X-ray cross section is almost equal to that of the solvent: R= Dilution Ratio

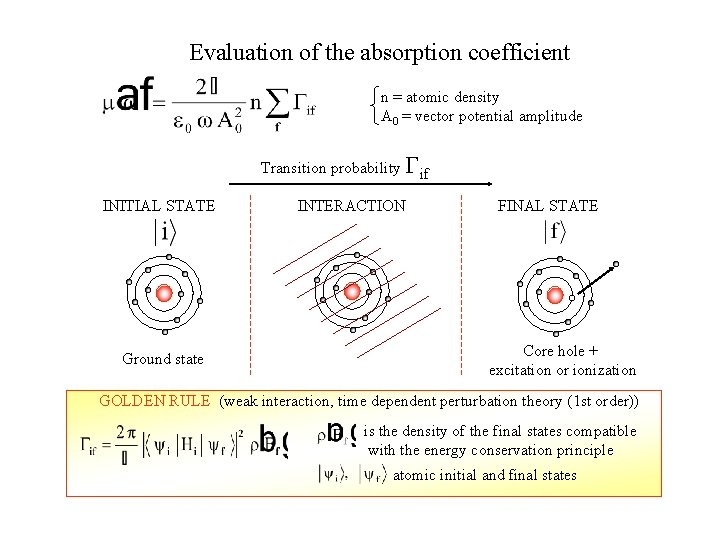
Evaluation of the absorption coefficient n = atomic density A 0 = vector potential amplitude Transition probability Gif INITIAL STATE Ground state INTERACTION FINAL STATE Core hole + excitation or ionization GOLDEN RULE (weak interaction, time dependent perturbation theory (1 st order)) is the density of the final states compatible with the energy conservation principle atomic initial and final states

Interaction Hamiltonian j = electrons; = polarization unit vector; An equivalent expression often used is: = radiation wavevector Electric dipole approximation This approximation is valid if: i. e. for the K edges for energies up to 25 - 30 K e. V and for the L edges Selection rules:

The direct and inverse problem Direct problem: Inverse problem In practice one is interested to the inverse problem. Given: , experimentally determined, one wants to know from XAFS, the final state But also in this case one needs to know the initial and final states or, at least , to express in parametric form the interesting structural properties. is known because it is the fundamental state of the atom. The calculation of is complicated because the absorption process because: • Many bodies interactions • The final state is influenced by the environment around the absorption atom

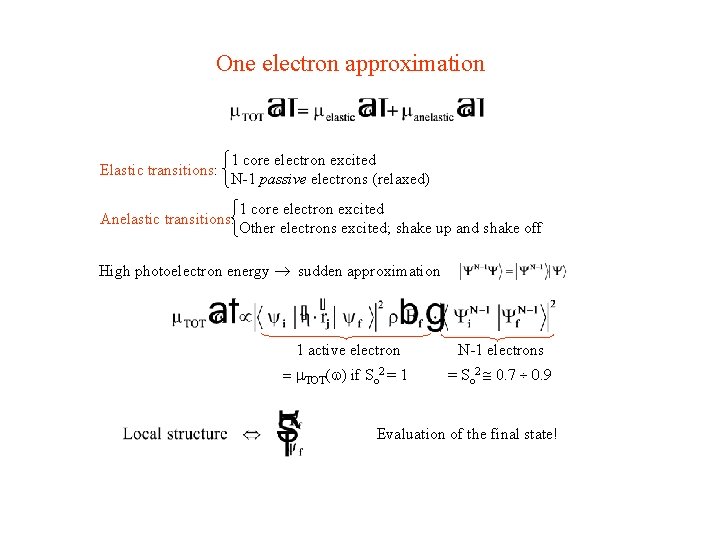
One electron approximation Elastic transitions: 1 core electron excited N-1 passive electrons (relaxed) Anelastic transitions: 1 core electron excited Other electrons excited; shake up and shake off High photoelectron energy ® sudden approximation 1 active electron N-1 electrons = TOT(w) if So 2 = 1 = So 2 @ 0. 7 ¸ 0. 9 Evaluation of the final state!

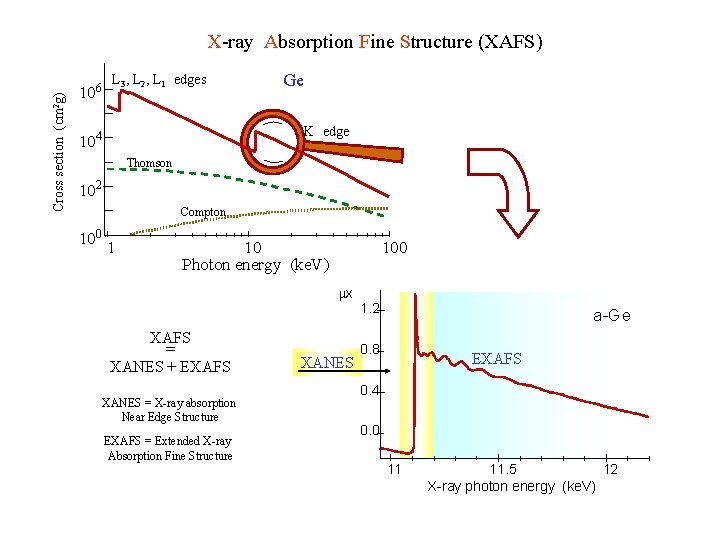
Cross section (cm 2 g) X-ray Absorption Fine Structure (XAFS) 10 6 L 3, L 2, L 1 edges Ge K edge 104 Thomson 102 Compton 100 1 10 Photon energy (ke. V) 100 x 1. 2 XAFS = XANES + EXAFS XANES = X-ray absorption Near Edge Structure EXAFS = Extended X-ray Absorption Fine Structure XANES a-Ge 0. 8 EXAFS 0. 4 0. 0 11 11. 5 12 X-ray photon energy (ke. V)

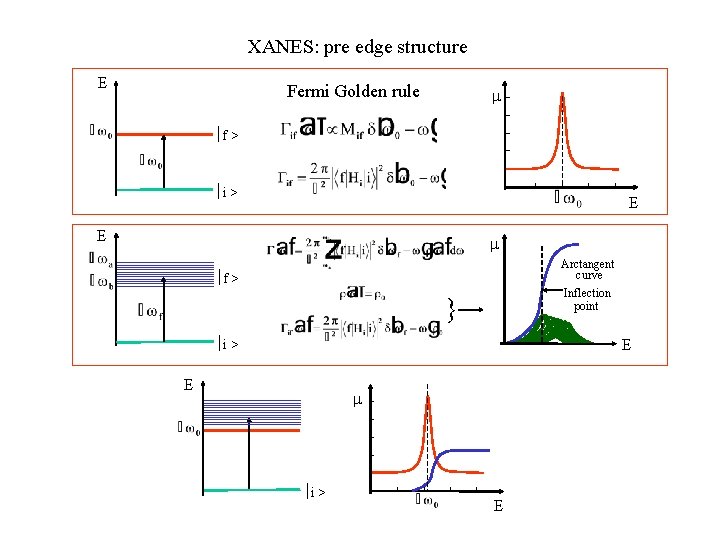
XANES: pre edge structure E Fermi Golden rule ½f > ½i > E E Arctangent curve ½f > Inflection point } ½i > E E ½i > E

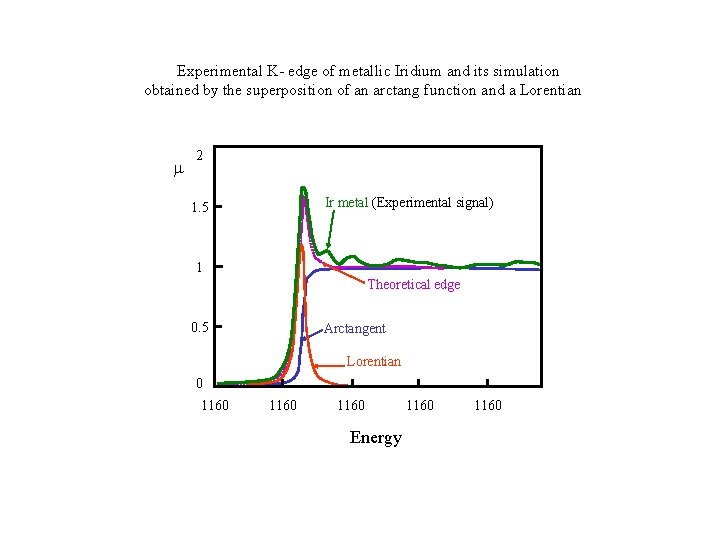
Experimental K- edge of metallic Iridium and its simulation obtained by the superposition of an arctang function and a Lorentian 2 Ir metal (Experimental signal) 1. 5 1 Theoretical edge 0. 5 Arctangent Lorentian 0 1160 Energy 1160

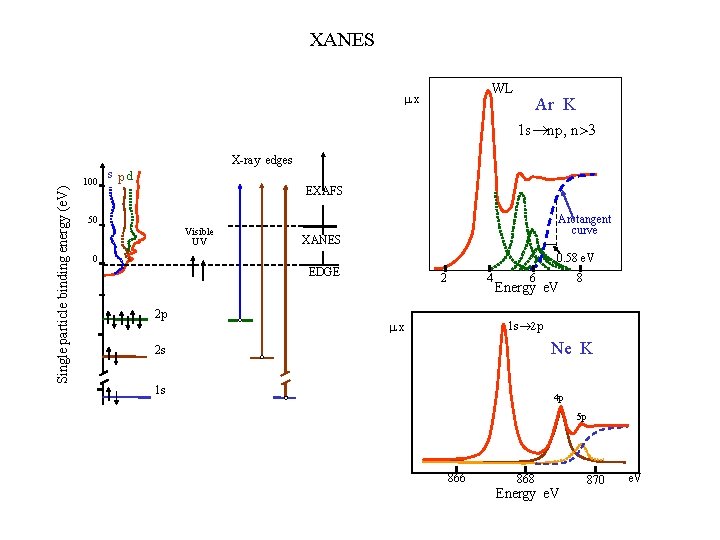
XANES WL x Ar K 1 s®np, n>3 Single particle binding energy (e. V) X-ray edges s pd 100 EXAFS Arctangent curve 50 Visible UV XANES 0. 58 e. V 0 EDGE 2 p 2 4 x 6 Energy e. V 8 1 s® 2 p Ne K 2 s 1 s 4 p 5 p 866 868 Energy e. V 870 e. V

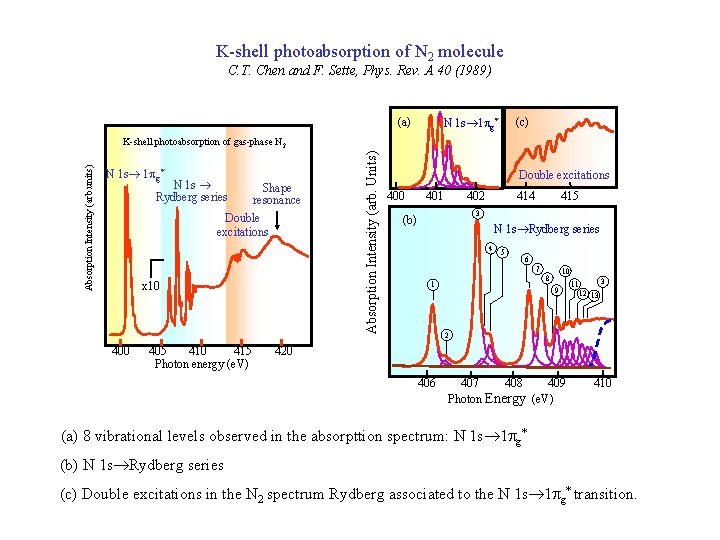
K-shell photoabsorption of N 2 molecule C. T. Chen and F. Sette, Phys. Rev. A 40 (1989) (a) (c) N 1 s® 1 pg* N 1 s ® Rydberg series Shape resonance Double excitations x 10 405 410 415 Photon energy (e. V) Absorption Intensity (arb. Units) Absorption Intensity (arb. units) K-shell photoabsorption of gas-phase N 2 Double excitations 400 401 402 414 415 3 (b) N 1 s®Rydberg series 4 5 6 7 10 8 1 9 3 11 12 13 2 420 406 407 408 409 Photon Energy (e. V) 410 (a) 8 vibrational levels observed in the absorpttion spectrum: N 1 s® 1 pg* (b) N 1 s®Rydberg series (c) Double excitations in the N 2 spectrum Rydberg associated to the N 1 s® 1 pg* transition.

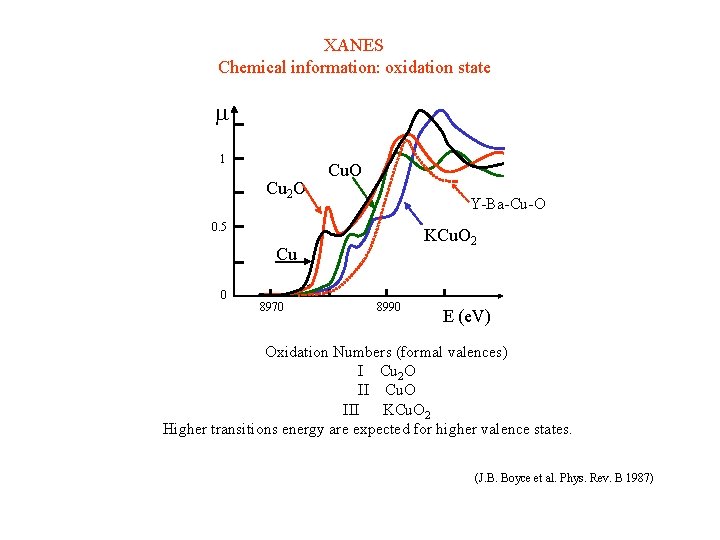
XANES Chemical information: oxidation state 1 Cu 2 O Cu. O Y-Ba-Cu-O 0. 5 KCu. O 2 Cu 0 8970 8990 E (e. V) Oxidation Numbers (formal valences) I Cu 2 O II Cu. O III KCu. O 2 Higher transitions energy are expected for higher valence states. (J. B. Boyce et al. Phys. Rev. B 1987)

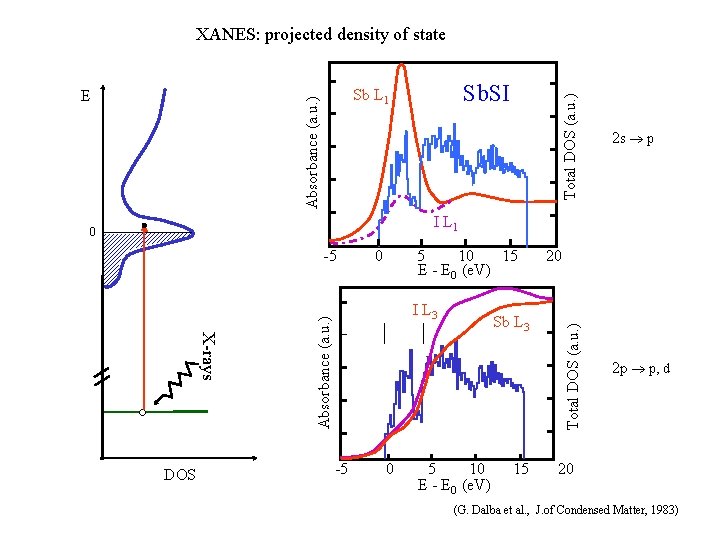
XANES: projected density of state Total DOS (a. u. ) Sb. SI Sb L 1 Absorbance (a. u. ) E 2 s ® p I L 1 -5 5 10 15 E - E 0 (e. V) I L 3 Absorbance (a. u. ) X-rays DOS 0 -5 0 Sb L 3 5 10 E - E 0 (e. V) 15 20 Total DOS (a. u. ) 0 2 p ® p, d 20 (G. Dalba et al. , J. of Condensed Matter, 1983)

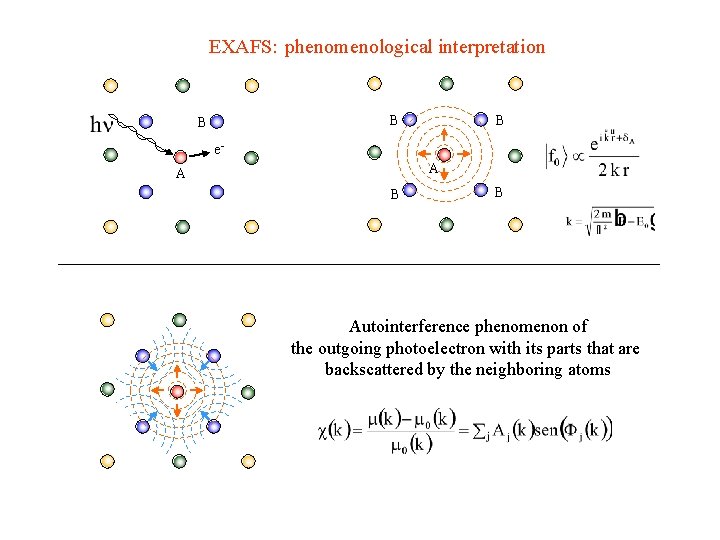
EXAFS: phenomenological interpretation B B B e. A A B B Autointerference phenomenon of the outgoing photoelectron with its parts that are backscattered by the neighboring atoms

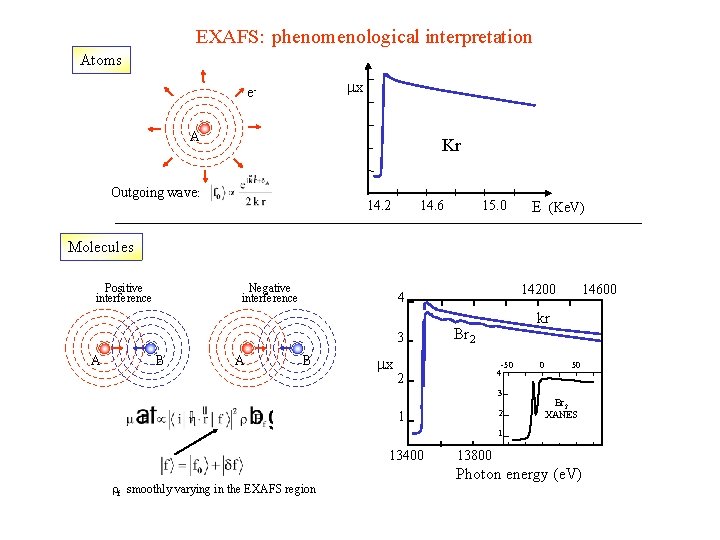
EXAFS: phenomenological interpretation Atoms x e. A Kr Outgoing wave: 14. 2 14. 6 15. 0 E (Ke. V) Molecules Positive interference Negative interference 3 A B A 14200 4 B x kr Br 2 -50 4 2 3 2 1 14600 0 50 Br 2 XANES 1 13400 rf smoothly varying in the EXAFS region 13800 Photon energy (e. V)

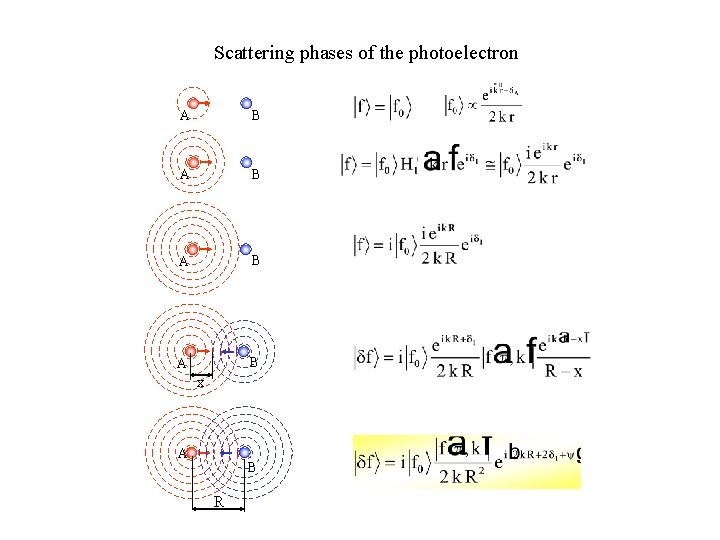
Scattering phases of the photoelectron A B A B x A B R
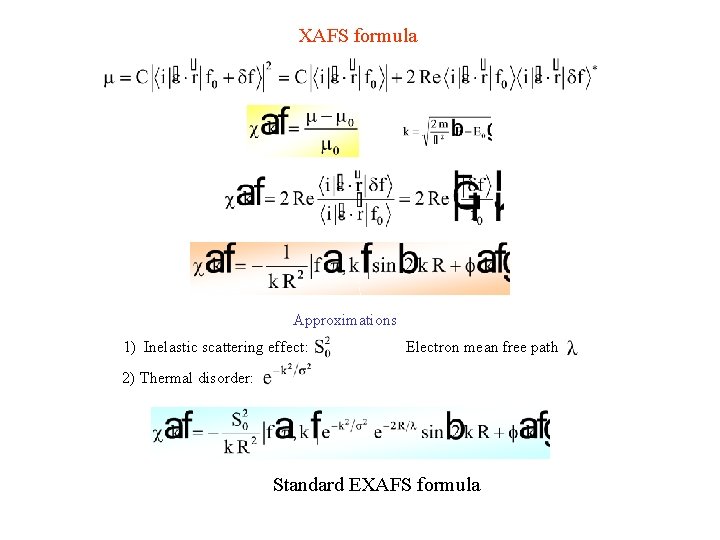
XAFS formula Approximations 1) Inelastic scattering effect: Electron mean free path 2) Thermal disorder: Standard EXAFS formula

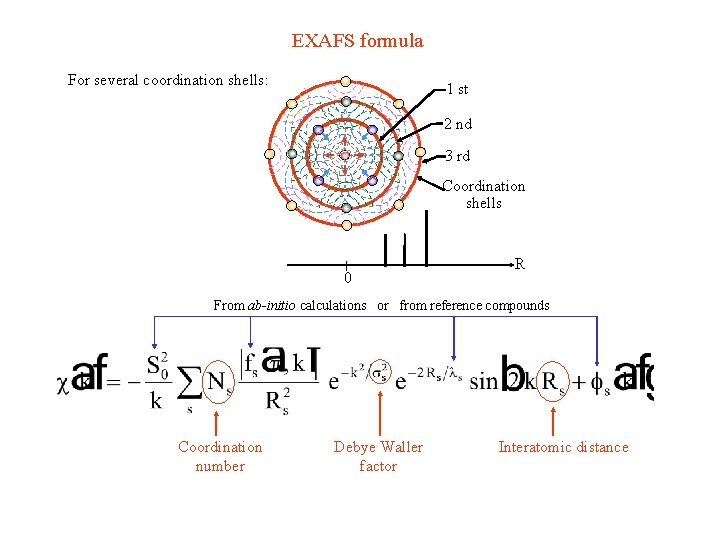
EXAFS formula For several coordination shells: 1 st 2 nd 3 rd Coordination shells 0 R From ab-initio calculations or from reference compounds Coordination number Debye Waller factor Interatomic distance

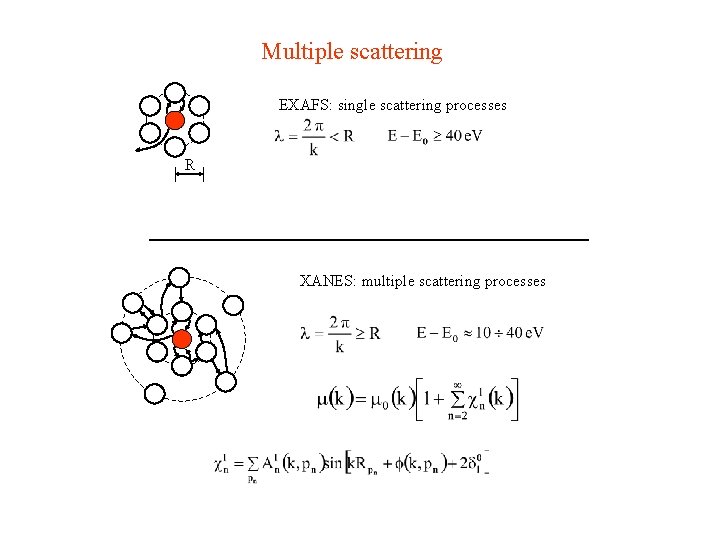
Multiple scattering EXAFS: single scattering processes R XANES: multiple scattering processes

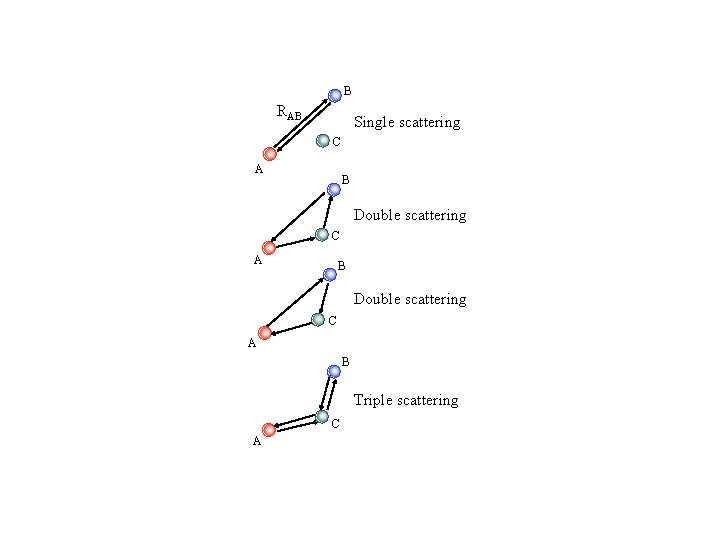
B RAB Single scattering C A B Double scattering C A B Triple scattering C A

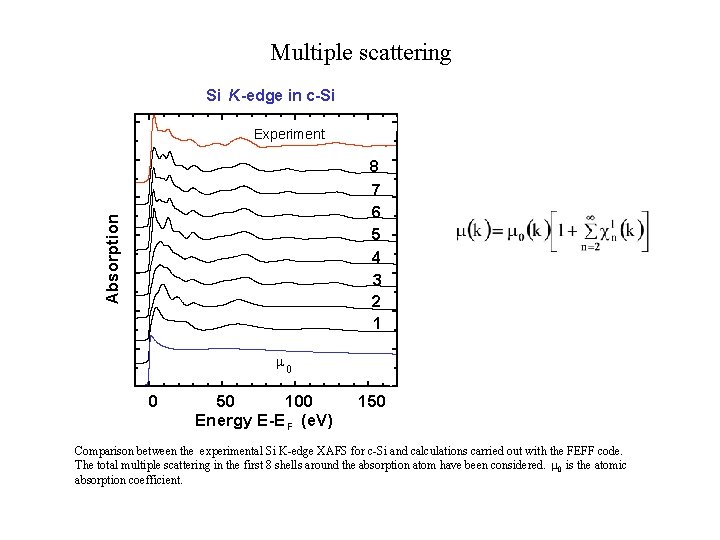
Multiple scattering Si K-edge in c-Si Experiment Absorption 8 7 6 5 4 3 2 1 0 0 50 100 Energy E-E F (e. V) 150 Comparison between the experimental Si K-edge XAFS for c-Si and calculations carried out with the FEFF code. The total multiple scattering in the first 8 shells around the absorption atom have been considered. 0 is the atomic absorption coefficient.