Interaction Terms and dummy variables in Regression Dummy

Interaction Terms and dummy variables in Regression

Dummy variables • Dichotomous independent variables – Takes value of 0 or 1 – Gender = female (yes or no); Democrat (yes or no); South (yes or no); Klingon v Earthling; etc.

Interactions between variables • Effect of one X variable may depend another X variable – Effect of X 1 conditional on X 2 – Effect of education on income may depend on gender (dummy variable) or age.

Interactions • Tested with OLS regression • Easiest to understand when a dichotomous (dummy, categorical) variable interacted with a interval variable – Also works with continuous * continuous

First, a dummy variable example • Data used is fake and includes the following variables as follows: – – Race (Klingon = 0, Earthling = 1) Education (4 <–> 16 years) Age (25 <–> 60) Income (100 <–> 280 dollars) – Income is Dependent variable

Initial Model No interaction here: Each X variable is estimated to have its own independent association with Y (income)

Initial Model Recall, how is t statistic calculated? How do we know if slope (Coef. ) is significantly different than 0?

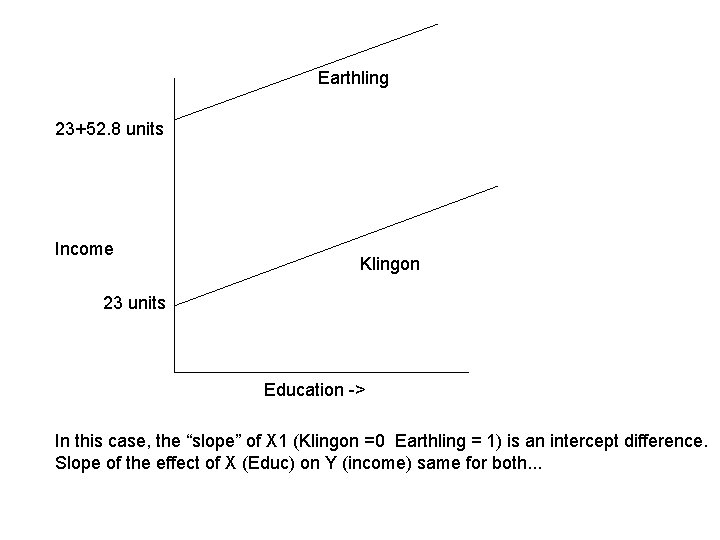
Earthling 23+52. 8 units Income Klingon 23 units Education -> In this case, the “slope” of X 1 (Klingon =0 Earthling = 1) is an intercept difference. Slope of the effect of X (Educ) on Y (income) same for both. . .

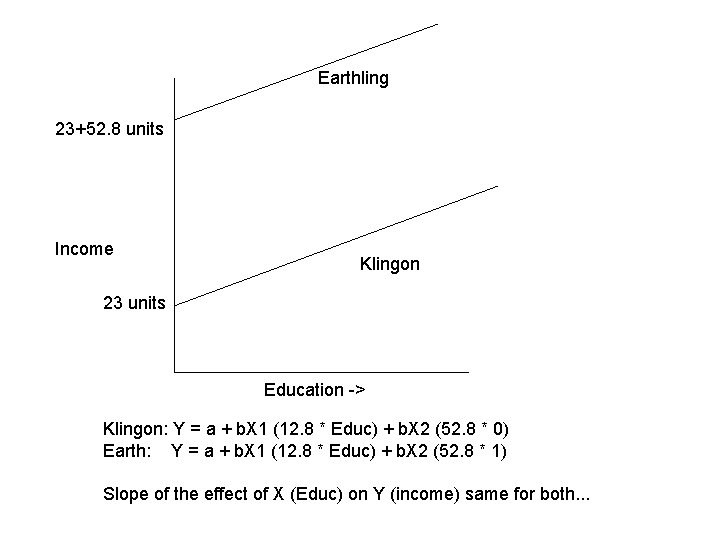
Earthling 23+52. 8 units Income Klingon 23 units Education -> Klingon: Y = a + b. X 1 (12. 8 * Educ) + b. X 2 (52. 8 * 0) Earth: Y = a + b. X 1 (12. 8 * Educ) + b. X 2 (52. 8 * 1) Slope of the effect of X (Educ) on Y (income) same for both. . .

Interactive Model • Does education affect income differently by race? • Find out by multiplying observations for Education by observations by race • Educationi * Earthlingi

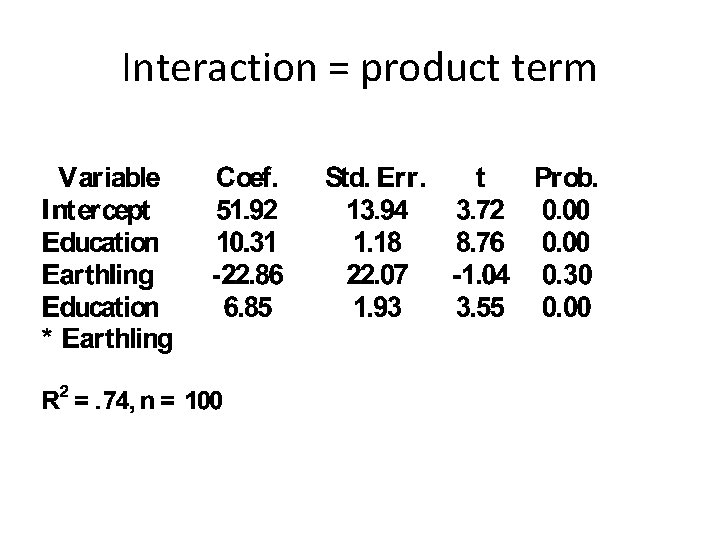
Interaction = product term

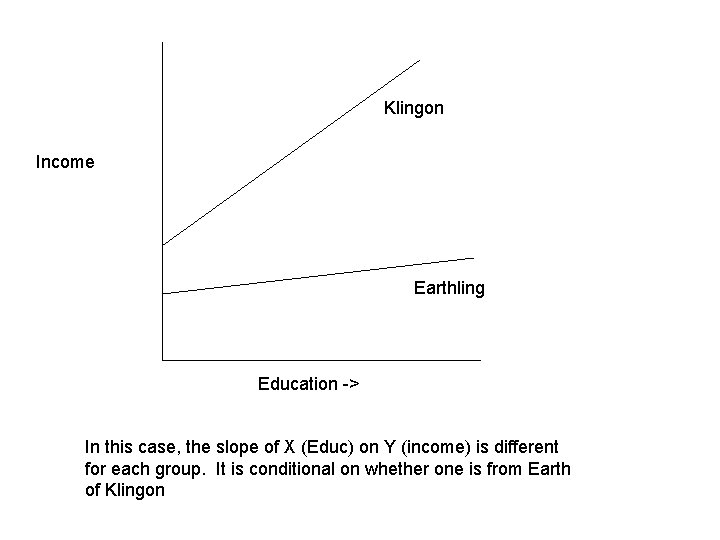
Klingon Income Earthling Education -> In this case, the slope of X (Educ) on Y (income) is different for each group. It is conditional on whether one is from Earth of Klingon

Specification • DO NOT omitting variables that are part of the interaction – All variables that are part of the interaction stay in the equation – e. g. , don’t drop the Education and Earthling variables while leaving in Education * Earthling

F-test • Omitting variables. • Not performing an F-test – Need to know if interaction contributes to model

F-Test Formula The F-test formula is where k denotes the number of variables, subscript 1 refers to original model and subscript 2 refers to the expanded model.

F-Test = (. 74 -. 70)/(3 -2) (1 -. 74)/(100 -3 -1) = 14. 8 Critical value for F < 3. 84 14. 8 > 3. 84 so interactive model is statistically significant

Evaluating the Overall Model • Interactive terms lessen parsimony, increase difficulty of interpretation. • Don’t do unless the interactive adds explanatory power. • For OLS perform an F-test.