Interaction des rayonnements avec la matire 1 Particules

Interaction des rayonnements avec la matière- 1 Particules chargées IAEA Jour 2 – Leçon 1 1

Objectif • Comprendre les interaction suivantes des particules chargées: Ø Mécanismes de transfert de l’énergie Ø Gammes d’énergies Ø Courbe de Bragg Ø Pouvoir d’arrêt Ø Blindage IAEA 2

Mécanismes de transfert d’énergie Le transfert d'énergie de particules radioactives à d'autres matériaux dépend: Ø du type et de l’énergie du rayonnement Ø De la nature milieu absorbant • Le rayonnement peut interagir aussi bien avec le noyau d’un atome qu’avec les électrons du cortège électronique • Les résultats de l’interaction est l’excitation et l’ionisation des atomes absorbants IAEA 3

Interactions des Particules Ø Lorsqu’une particule interagit avec un atome d’un absorbant, il peut: v Interagir par collision (avec les électrons) v Interagir par freinage (avec le noyau) Ø Une forte collision entre deux particules de même masse entraine le transfert d’une grande quantité d'énergie à la matière IAEA 4

Pouvoir d’arrêt Ø La quantité d'énergie déposée sera la somme des énergies déposées par collision et par freinage Ø Le pouvoir d’arrêt est la somme des énergies déposées par collision et par freinage Ø les interactions avec les électrons atomiques sont prédominantes, elles s’accompagnent chaque fois d’un transfert d’énergie. La probabilité d’interaction avec le noyau est faible, il faut que l’énergie de la particule incidente soit suffisante. IAEA 5

Pouvoir d’arrêt • Le pouvoir d’arrêt est fonction de la charge de la particule, de l'énergie de la particule, et du matériau avec lequel les particules chargées interagissent IAEA 6

Pouvoir d’arrêt • Le pouvoir d’arrêt s’exprime en Me. V/cm • La quantité d’énergie déposée par cm du milieu traversé par la particule • C’est la somme des énergies déposées par collision et par freinage. S= IAEA d. E dx = Tot d. Es dx + d. Eh dx 7

Pouvoir d’arrêt Massique • Souvent, le pouvoir d’arrêt est divisé par la densité du matériau, • C’est ce qu’on appelle ″le pouvoir d’arrêt massique″ • La dimension du pouvoir d’arrêt massique est: Me. V – cm 2 g IAEA 8

Pouvoir d’arrêt Le pouvoir d’arrêt massique est utiliser pour déterminer l’énergie perdue par unité de masse: D= d. E dx en Me. V/g, où = fluence de particules, le nombre de particules tapant un objet pendant un intervalle de temps spécifié IAEA 9

Pouvoir d’arrêt Pour la conversion en unité de dose nous procédons de la manière suivant: D= d. E dx Me. V/g = d. E dx (1. 6 x 10 -10) Gy 1 ev = 1. 6 X 10 -19 J IAEA 10

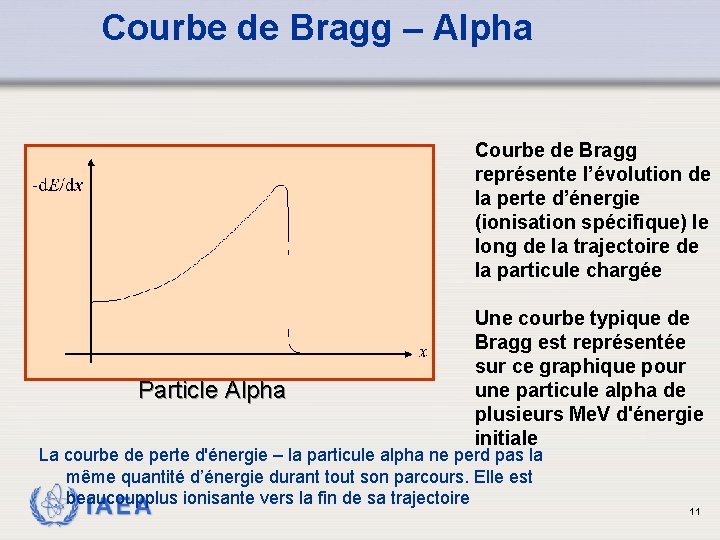
Courbe de Bragg – Alpha Courbe de Bragg représente l’évolution de la perte d’énergie (ionisation spécifique) le long de la trajectoire de la particule chargée Particle Alpha Une courbe typique de Bragg est représentée sur ce graphique pour une particule alpha de plusieurs Me. V d'énergie initiale La courbe de perte d'énergie – la particule alpha ne perd pas la même quantité d’énergie durant tout son parcours. Elle est beaucoupplus ionisante vers la fin de sa trajectoire IAEA 11

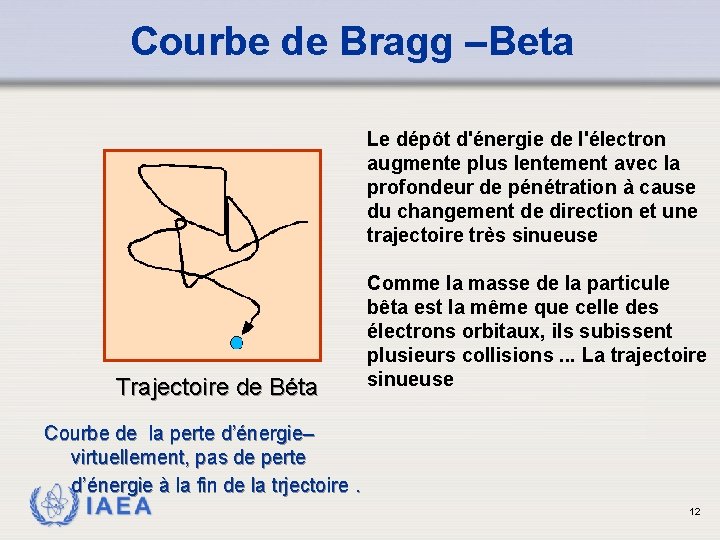
Courbe de Bragg –Beta Le dépôt d'énergie de l'électron augmente plus lentement avec la profondeur de pénétration à cause du changement de direction et une trajectoire très sinueuse Trajectoire de Béta Comme la masse de la particule bêta est la même que celle des électrons orbitaux, ils subissent plusieurs collisions. . . La trajectoire sinueuse Courbe de la perte d’énergie– virtuellement, pas de perte d’énergie à la fin de la trjectoire. IAEA 12

Parcours – Particules Béta • Dépend de l’énergie de la particule béta et de la densité du milieu absorbeur Ø L’Énergie des particules bêta diminue à mesure que la densité du milieu traversé augmente • Les analyses expérimentales montrent que la capacité d'absorber des particules bêta: Ø Dépend de la densité d’électrons (électrons par cm 2) sur la trajectoire du rayon bêta Ø Moindre pour le numéro atomique de l'absorbeur IAEA 13

Parcours – en fonction de l’énergie • Atténuation des particules béta Ø En Interposant des écrans d‘un absorbeur entre une source bêta et détecteur: Ø Le nombre de particules béta o Diminue rapidement au début o plus lentement à mesure que l'épaisseur de l’absorbeur augmente o S’arrêtent complétement après une certaaine épaisseur de l’absorbeur Ø Le parcours de la particule béta – c’est l’épaisseur du milieu absorbeur qui arrête toutes les particules IAEA 14

Parcours – Particules Béta • La densité aérienne est liée à la densité de l'absorbeur td g/cm 2 = ρ (densité de l’absorbeur) g/cm 3 X tl (épaisseur de l’absorbeur) cm • Les écrans de protection pour les particules béta sont formés de matériaux de faible Z IAEA 15

Parcours – Particules Béta • Calculer la densité surfacique pour une épaisseur de 1 cm d’aluminium. Note: (Densité de Al = 2. 7 g/cm 3) IAEA 16

Parcours – Particules Béta • Calculer la densité surfacique pour une épaisseur de 1 cm d’aluminium. td g/cm 2 = ρ g/cm 3 X tl cm td = 2. 7 g/cm 2 • Un graphique de l'énergie bêta en fonction de l’épaisseur, de densité est utile pour le blindage et l'identification de la source bêta IAEA 17

Parcours – Particules Alpha • Les particules Alpha sont moins pénétrantes que les autres types de rayonnements • Les particules Alpha sont mono-énergétiques. Par conséquent, le nombre de particules alpha ne se réduit pas jusqu'à élimination totale par une épaisseur particulière de l'absorbeur. • L’épaisseur qui arrête toutes les particules alpha est le parcours de la particule dans le matériau. • Les particules plus énergétiques traversent quelques cm dans l’air, et quelques µm dans les tissus. IAEA 18

Transfert Linéique de l’Energie TLE: est la quantité d’énergie transférée au milieu cible par la particule incidente par unité de longueur de la trajectoire. LET = d. E dx ke. V/µm d. E = est l'énergie moyenne communiquée par le rayonnement de l'énergie spécifique en parcourant une distance de dx. IAEA 19

Transfert Linéique de l’Energie • L’ionisation spécifique est le nombre de paires d'ions formées par unité de distance parcourue par la particule. Ce concept est très utile en radioprotection. • L’ionisation spécifique est très élevée pour les particules bêta de faible énergie et diminue à mesure que l'énergie augmente. • L’ionisation spécifique est très élevée pour les particules alpha. • En traversant l’air ou les tissus, les particules alpha perdent en moyenne 35 e. V par paire d’ion crée. • La charge électrique élevée et la faible vitesse signifient des dizaines de milliers de paires d'ions par cm d'air se sont crées. IAEA 20

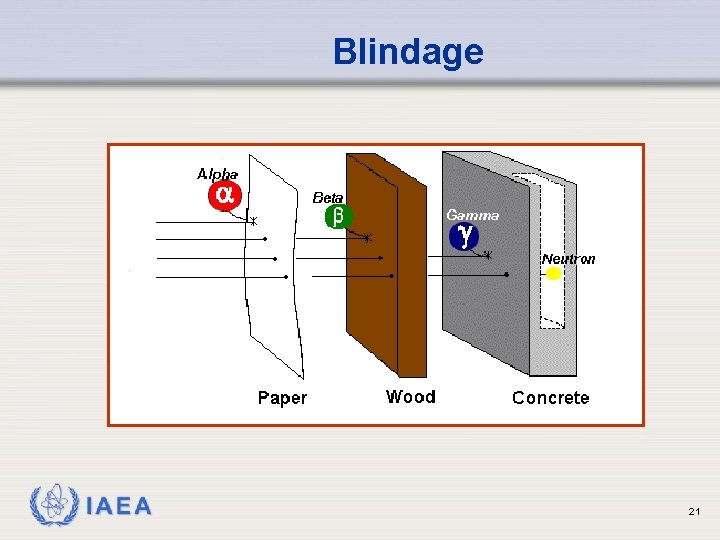
Blindage IAEA 21

Dose Absorbée ØC’est l’énergie déposée par unité de masse de la matière Ø L’unité de la dose absorbée est Gray (Gy) (1 Gray = 1 joule/kg) ØPour calculer la dose due aux particules chargées, nous devons déterminer la quantité d'énergie déposée par gramme de matière IAEA 22

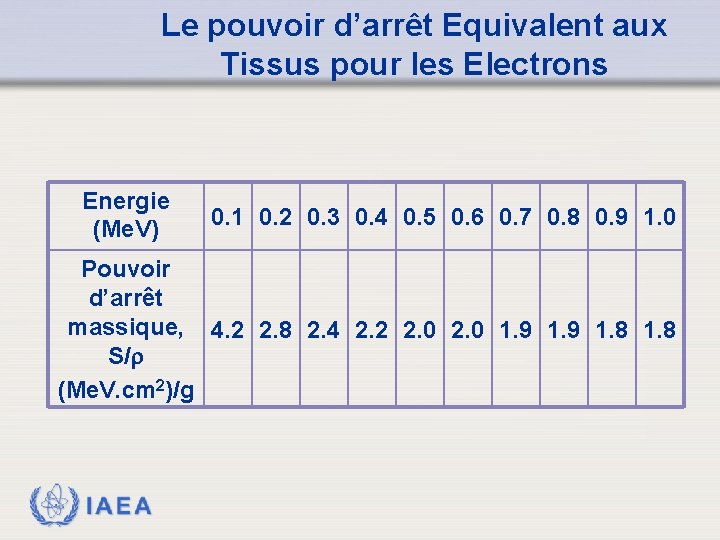
Le pouvoir d’arrêt Equivalent aux Tissus pour les Electrons Energie (Me. V) 0. 1 0. 2 0. 3 0. 4 0. 5 0. 6 0. 7 0. 8 0. 9 1. 0 Pouvoir d’arrêt massique, 4. 2 2. 8 2. 4 2. 2 2. 0 1. 9 1. 8 S/ (Me. V. cm 2)/g IAEA

Exemple Calculer la dose délivrée par une contamination de 37 000 Bq du 32 P, déposée sur une surface de 1 cm 2 de la peau d’un individu pendant 1 heure d. E D= dx (1. 6 x 10 -10) Gy 32 P émet des particules béta de 0. 690 Me. V (énergie moyenne). On suppose que 50% (1/2) des particules déposées interagissent avec la peau IAEA 24

Pouvoir d’arrêt -Exemple = (½)(37. 000 Bq)(1 dés. /s/Bq)(1 h)(3600 s/h) = 6. 67 x 107 dés. 32 P émet des particules béta d’une énergie moyenne de 0. 690 Me. V Pour le plastique équivalent aux tissus, et une particule bêta d’une énergie de 0. 690 Me. V, le pouvoir d’arrêt massique est de 1. 96 Me. V. cm 2/g IAEA 25

Pouvoir d’arrêt -Exemple d. E D= dx Me. V. cm 2/g D = 6. 67 x 107 X 1. 96 X 1. 6 x 10 -10 J/kg D = 0. 021 Gy IAEA 26

Where to Get More Information Ø Cember, H. , Johnson, T. E, Introduction to Health Physics, 4 th Edition, Mc. Graw-Hill, New York (2009) Ø International Atomic Energy Agency, Postgraduate Educational Course in Radiation Protection and the Safety of Radiation Sources (PGEC), Training Course Series 18, IAEA, Vienna (2002) IAEA 27