Inter Block Backtracking Exploiting Structure in Numerical CSPs

Inter. Block. Backtracking: Exploiting Structure in Numerical CSPs Solving Christophe Jermann LINA/CNRS, University of Nantes Joint work with: Bertrand Neveu, Gilles Trombettoni I 3 S/CNRS-INRIA, University of Nice

Outline m IBB: a general framework for solving decomposed NCSPs m m m Principle Inputs Process m IBB+Interval: m m m an instance of IBB Interval solving Interblock Filtering Experiments m Conclusion & Future directions

Outline m IBB: a general framework for solving decomposed NCSPs m m m Principle Inputs/Parameters Process m IBB+Interval: m m m an instance of IBB Interval solving Interblock Filtering Experiments m Conclusion & Future directions
![IBB: general sight m Main ideas in [Bliek et al, CP 98] m Since IBB: general sight m Main ideas in [Bliek et al, CP 98] m Since](http://slidetodoc.com/presentation_image_h2/5d36b6f463b5bf1513ebaa397930b3b4/image-4.jpg)
IBB: general sight m Main ideas in [Bliek et al, CP 98] m Since then, made a general framework m Parameters: fix to obtain one instance of IBB m m m a (set of) solving method(s) a backtracking process optional: a set of “add-ons” m Inputs: m a decomposed numerical CSP (NCSP) m Output: m One (or all the) solution(s) of the NCSP

Numerical CSPs m Defined m m m by (X, D, C) where: X: a set of variables D: a set of continuous domains, one for each x X C: a set of constraints (equations, inequalities, …) on X m Applications: m m m Physics: forces, electrical measurements… Design & Geometry: distances, angles, … Program verification: instructions with floats, … Robotics: kinematic constraints, … …

Decomposed NCSPs m Decomposed(S) = ({S 1, S 2, …, S 3}, <, +) Si = well-constrained sub-NCSP m < = partial order for Si’s solving m + = partial solutions combination operator Such that Sol(S 1)+Sol(S 2)+…+Sol(S 3) = Sol(S) m m Why m decompose ? Divide & conquer => reduce solving complexity m Several m m m kinds of decompositions : Equational [Michelucci et al. 1996], [Bliek et al. 1998], … Geometric [Hoffmann et al 1995], [Jermann et al. 2000], … …

Solving methods m NCSP system of (non-linear) equations/inequalities m Symbolic: Groebner basis, … m Numeric: Local (Newton-Raphson, …), Homotopy, Interval, … Generally, the structure is under-exploited IBB allows to generically exploit the structure identified by decomposition
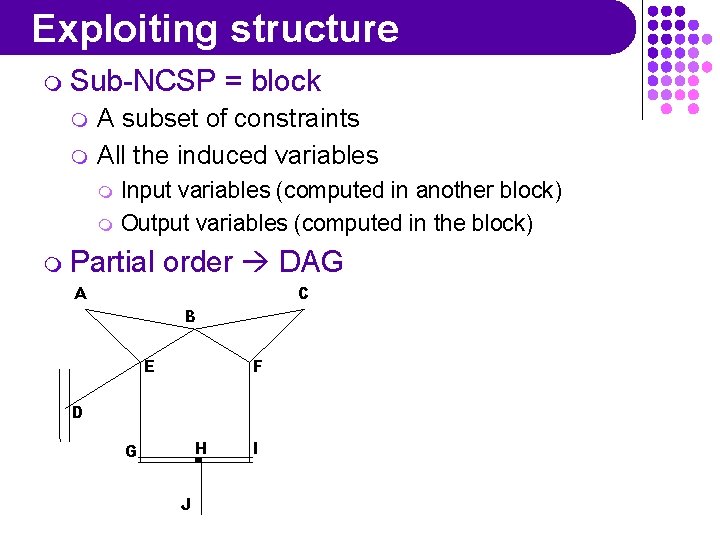
Exploiting structure m Sub-NCSP m m = block A subset of constraints All the induced variables m m Input variables (computed in another block) Output variables (computed in the block) m Partial order DAG A C B E F D H G J I
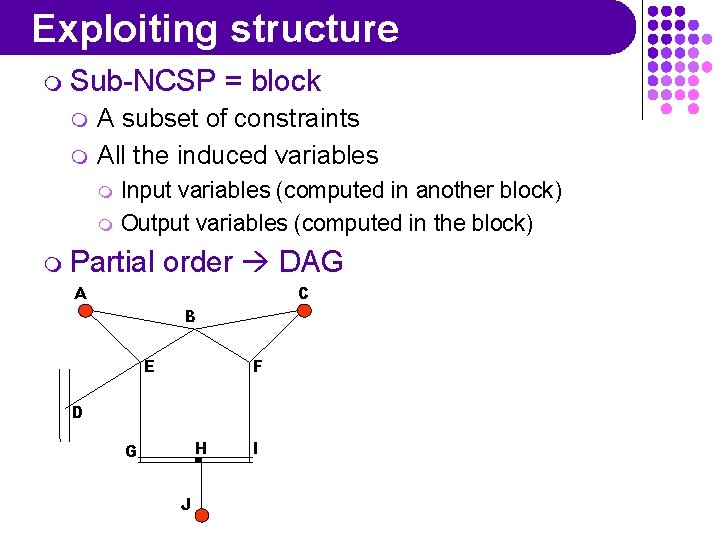
Exploiting structure m Sub-NCSP m m = block A subset of constraints All the induced variables m m Input variables (computed in another block) Output variables (computed in the block) m Partial order DAG A C B E F D H G J I
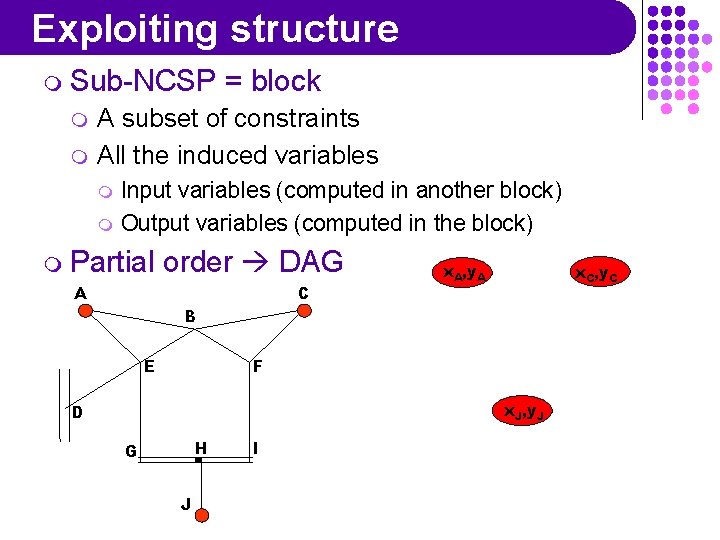
Exploiting structure m Sub-NCSP m m = block A subset of constraints All the induced variables m m Input variables (computed in another block) Output variables (computed in the block) m Partial order DAG A C x. A, y. A x. C, y. C B E F x. J, y. J D H G J I
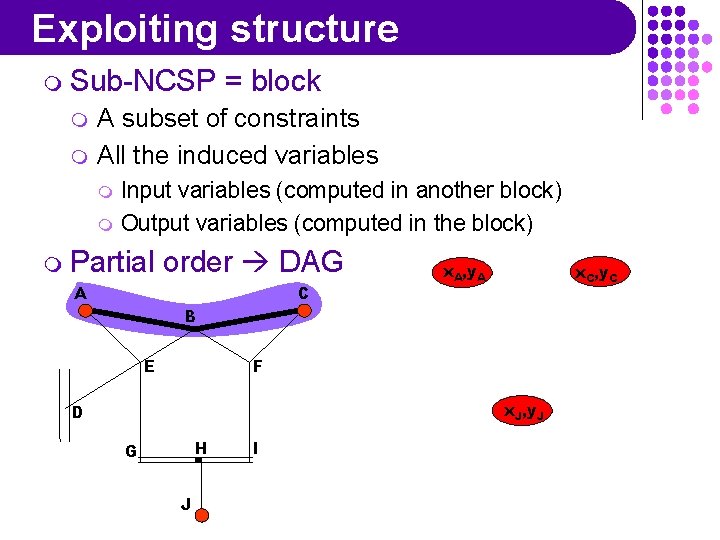
Exploiting structure m Sub-NCSP m m = block A subset of constraints All the induced variables m m Input variables (computed in another block) Output variables (computed in the block) m Partial order DAG A C x. A, y. A x. C, y. C B E F x. J, y. J D H G J I
Exploiting structure m Sub-NCSP m m = block A subset of constraints All the induced variables m m Input variables (computed in another block) Output variables (computed in the block) m Partial order DAG A C B E x. A, y. A x. C, y. C x. B, y. B F x. J, y. J D H G J I
Exploiting structure m Sub-NCSP m m = block A subset of constraints All the induced variables m m Input variables (computed in another block) Output variables (computed in the block) m Partial order DAG A C B E x. A, y. A x. C, y. C x. B, y. B F x. J, y. J D H G J I
Exploiting structure m Sub-NCSP m m = block A subset of constraints All the induced variables m m Input variables (computed in another block) Output variables (computed in the block) m Partial order DAG A C x. A, y. A B E x. C, y. C x. B, y. B F x. E, y. E D H G J I x. J, y. J
Exploiting structure m Sub-NCSP m m = block A subset of constraints All the induced variables m m Input variables (computed in another block) Output variables (computed in the block) m Partial order DAG A C x. A, y. A B E x. C, y. C x. B, y. B F x. E, y. E D H G J I x. J, y. J x. F, y. F
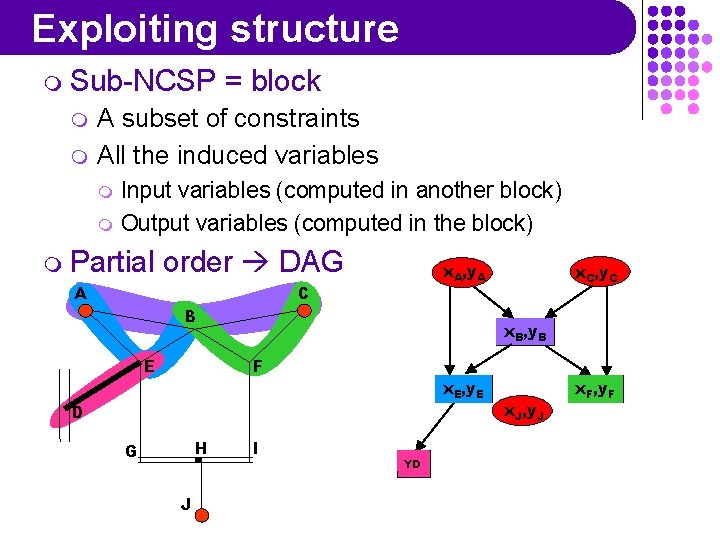
Exploiting structure m Sub-NCSP m m = block A subset of constraints All the induced variables m m Input variables (computed in another block) Output variables (computed in the block) m Partial order DAG A x. A, y. A C B E x. C, y. C x. B, y. B F x. E, y. E D H G J I YD x. J, y. J x. F, y. F
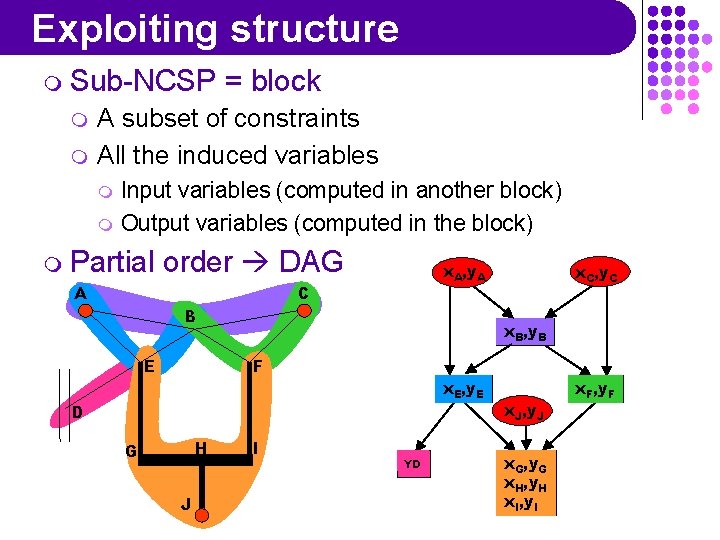
Exploiting structure m Sub-NCSP m m = block A subset of constraints All the induced variables m m Input variables (computed in another block) Output variables (computed in the block) m Partial order DAG A x. A, y. A C B E x. C, y. C x. B, y. B F x. E, y. E D H G J I YD x. J, y. J x. G, y. G x. H, y. H x. I, y. I x. F, y. F
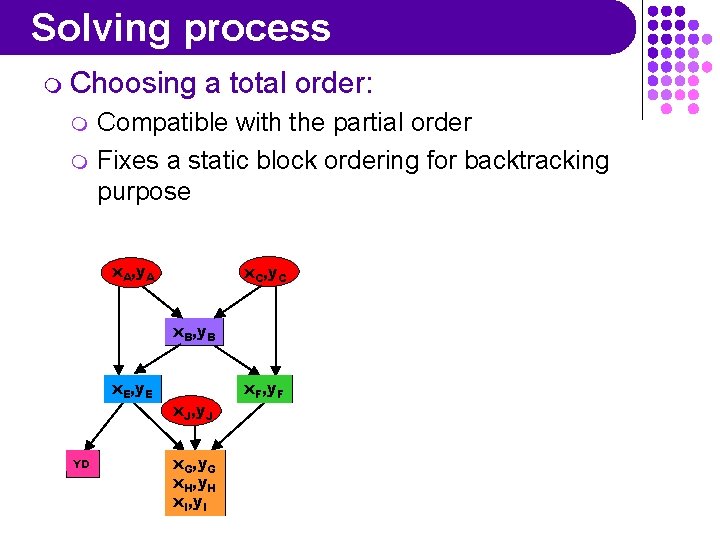
Solving process m Choosing m m a total order: Compatible with the partial order Fixes a static block ordering for backtracking purpose x. A, y. A x. C, y. C x. B, y. B x. E, y. E YD x. J, y. J x. G, y. G x. H, y. H x. I, y. I x. F, y. F
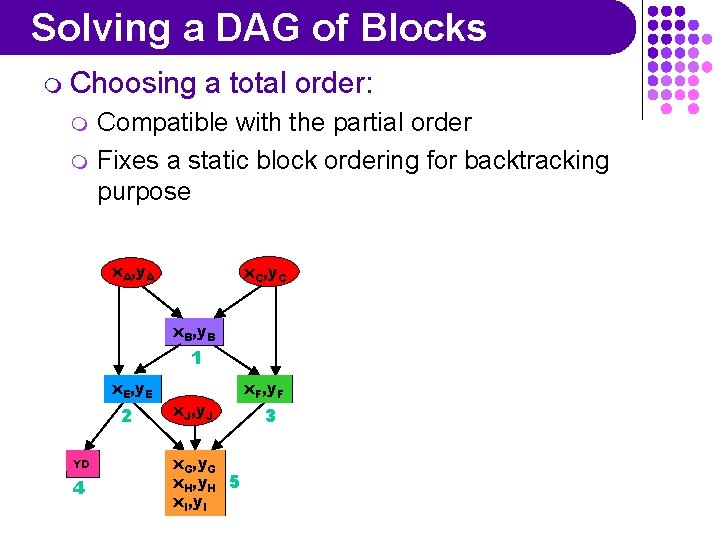
Solving a DAG of Blocks m Choosing m m a total order: Compatible with the partial order Fixes a static block ordering for backtracking purpose x. A, y. A x. C, y. C x. B, y. B 1 x. E, y. E 2 YD 4 x. J, y. J x. G, y. G x. H, y. H 5 x. I, y. I x. F, y. F 3
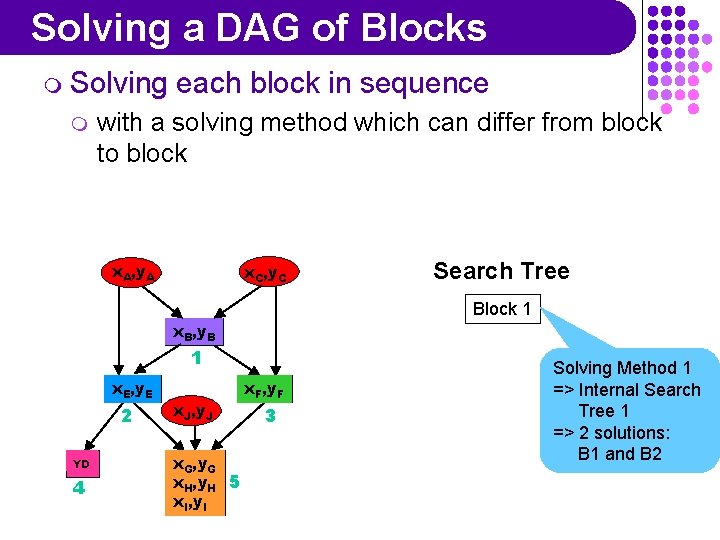
Solving a DAG of Blocks m Solving m each block in sequence with a solving method which can differ from block to block x. A, y. A x. C, y. C Search Tree Block 1 x. B, y. B 1 x. E, y. E 2 YD 4 x. J, y. J x. G, y. G x. H, y. H 5 x. I, y. I x. F, y. F 3 Solving Method 1 => Internal Search Tree 1 => 2 solutions: B 1 and B 2
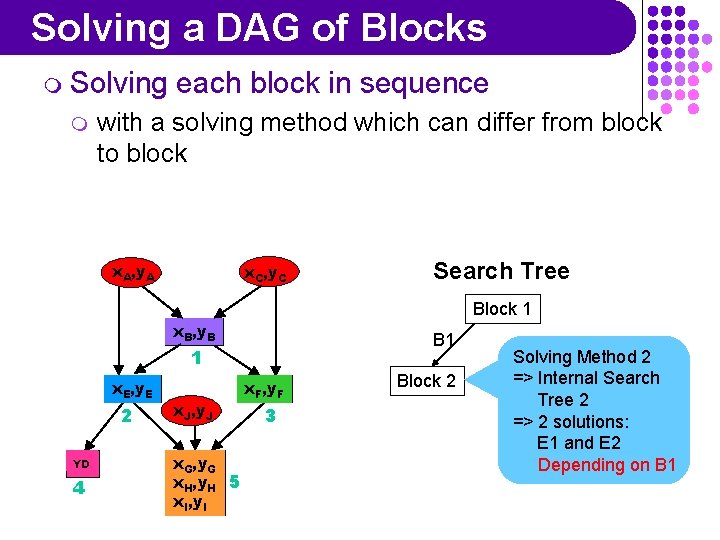
Solving a DAG of Blocks m Solving m each block in sequence with a solving method which can differ from block to block x. A, y. A x. C, y. C Search Tree Block 1 x. B, y. B B 1 1 x. E, y. E 2 YD 4 x. J, y. J x. G, y. G x. H, y. H 5 x. I, y. I x. F, y. F 3 Block 2 Solving Method 2 => Internal Search Tree 2 => 2 solutions: E 1 and E 2 Depending on B 1
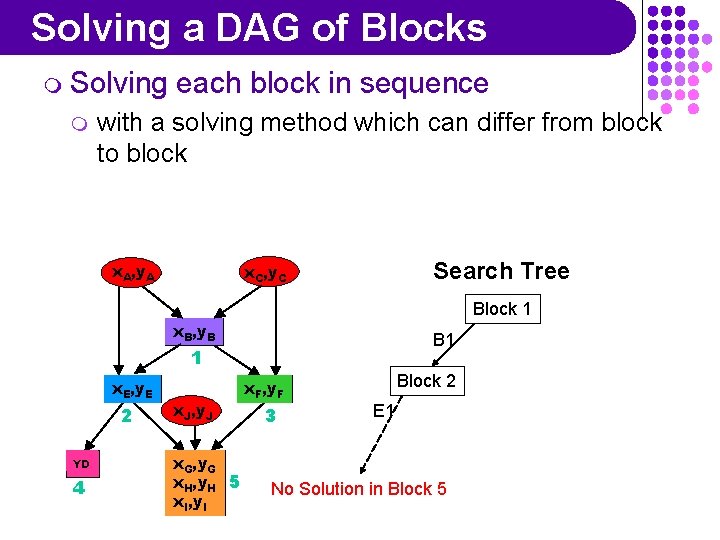
Solving a DAG of Blocks m Solving m each block in sequence with a solving method which can differ from block to block x. A, y. A Search Tree x. C, y. C Block 1 x. B, y. B B 1 1 x. E, y. E 2 YD 4 x. J, y. J x. G, y. G x. H, y. H 5 x. I, y. I x. F, y. F 3 Block 2 E 1 No Solution in Block 5
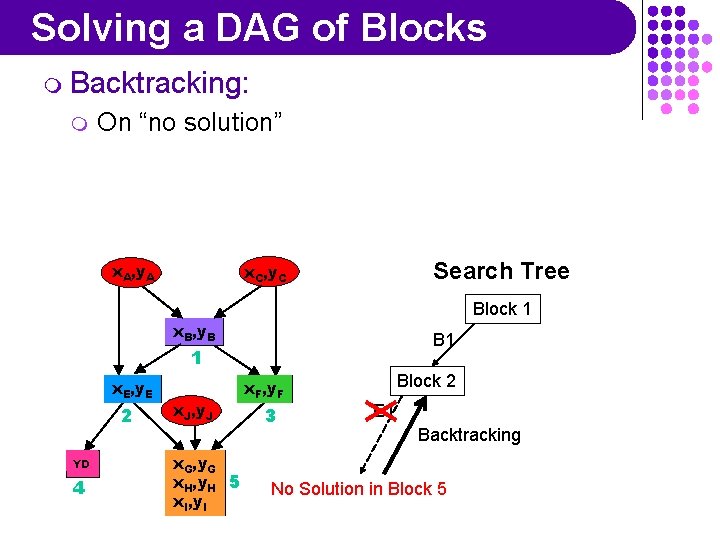
Solving a DAG of Blocks m Backtracking: m On “no solution” x. A, y. A Search Tree x. C, y. C Block 1 x. B, y. B B 1 1 x. E, y. E 2 YD 4 x. J, y. J x. G, y. G x. H, y. H 5 x. I, y. I x. F, y. F 3 Block 2 E 1 Backtracking No Solution in Block 5
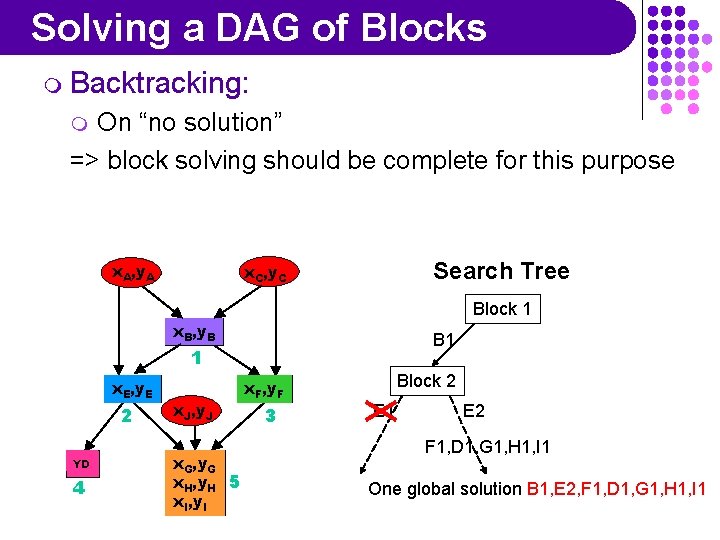
Solving a DAG of Blocks m Backtracking: On “no solution” => block solving should be complete for this purpose m x. A, y. A Search Tree x. C, y. C Block 1 x. B, y. B B 1 1 x. E, y. E 2 YD 4 x. J, y. J x. G, y. G x. H, y. H 5 x. I, y. I x. F, y. F 3 Block 2 E 1 E 2 F 1, D 1, G 1, H 1, I 1 One global solution B 1, E 2, F 1, D 1, G 1, H 1, I 1
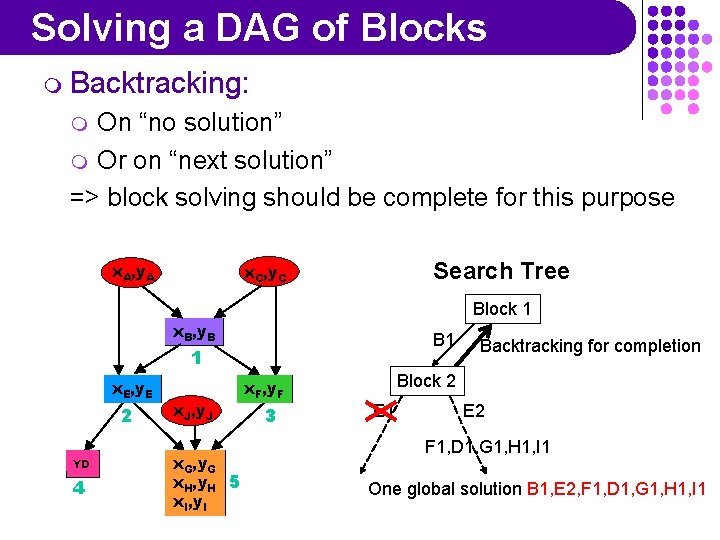
Solving a DAG of Blocks m Backtracking: On “no solution” m Or on “next solution” => block solving should be complete for this purpose m x. A, y. A Search Tree x. C, y. C Block 1 x. B, y. B B 1 1 x. E, y. E 2 YD 4 x. J, y. J x. G, y. G x. H, y. H 5 x. I, y. I x. F, y. F 3 Backtracking for completion Block 2 E 1 E 2 F 1, D 1, G 1, H 1, I 1 One global solution B 1, E 2, F 1, D 1, G 1, H 1, I 1
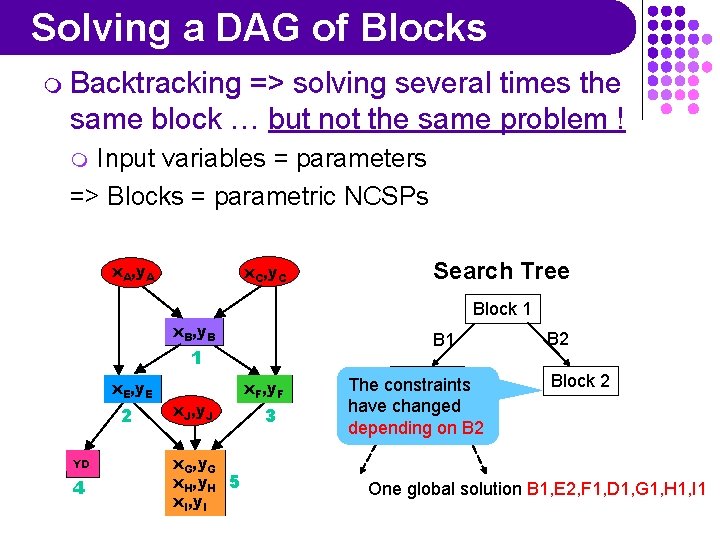
Solving a DAG of Blocks m Backtracking => solving several times the same block … but not the same problem ! Input variables = parameters => Blocks = parametric NCSPs m x. A, y. A x. C, y. C Search Tree Block 1 x. B, y. B B 1 1 x. E, y. E 2 YD 4 x. J, y. J x. G, y. G x. H, y. H 5 x. I, y. I x. F, y. F 3 Block 2 The constraints have E 1 changed E 2 depending on B 2 Block 2 One global solution B 1, E 2, F 1, D 1, G 1, H 1, I 1
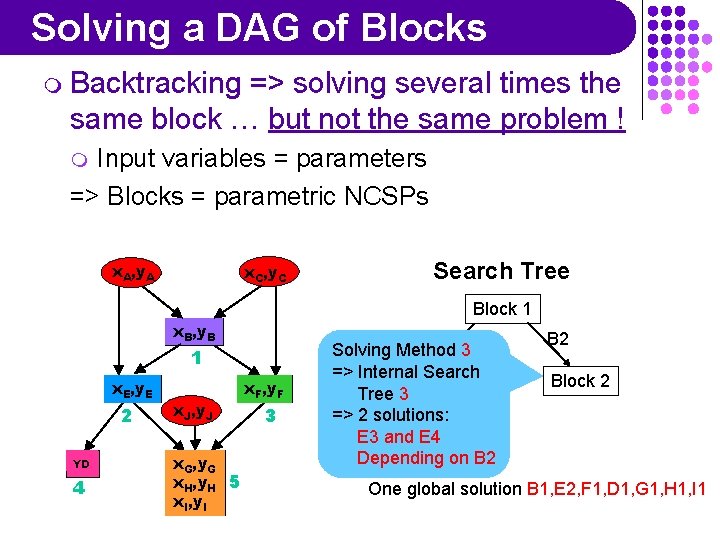
Solving a DAG of Blocks m Backtracking => solving several times the same block … but not the same problem ! Input variables = parameters => Blocks = parametric NCSPs m x. A, y. A x. C, y. C Search Tree Block 1 x. B, y. B 1 x. E, y. E 2 YD 4 x. J, y. J x. G, y. G x. H, y. H 5 x. I, y. I x. F, y. F 3 B 1 Solving Method 3 => Internal Search Block 2 Tree 3 => 2 E 1 solutions: E 2 E 3 and E 4 Depending on B 2 Block 2 One global solution B 1, E 2, F 1, D 1, G 1, H 1, I 1
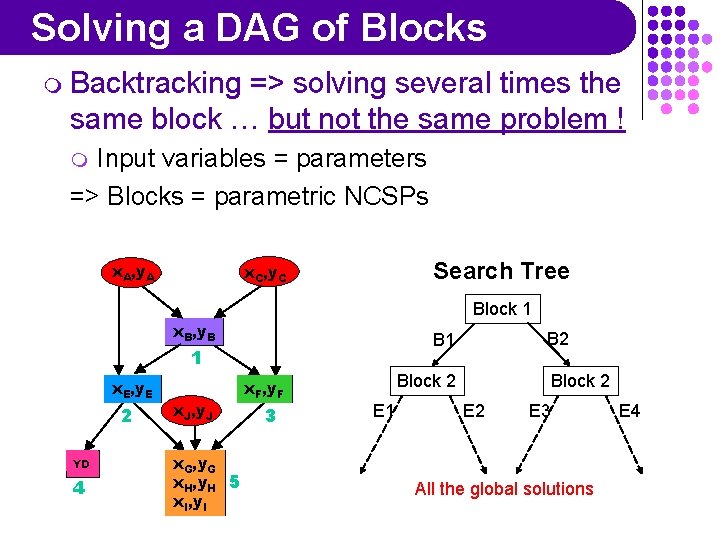
Solving a DAG of Blocks m Backtracking => solving several times the same block … but not the same problem ! Input variables = parameters => Blocks = parametric NCSPs m x. A, y. A Search Tree x. C, y. C Block 1 x. B, y. B 1 x. E, y. E 2 YD 4 x. J, y. J x. G, y. G x. H, y. H 5 x. I, y. I B 2 B 1 x. F, y. F 3 Block 2 E 1 Block 2 E 3 All the global solutions E 4
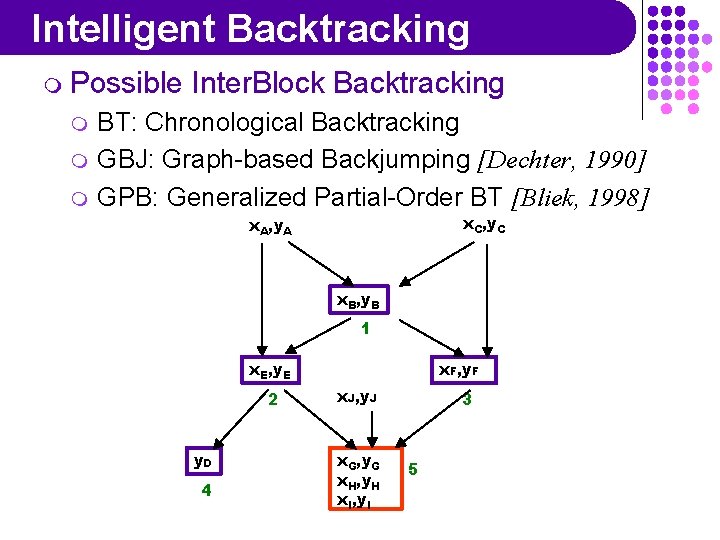
Intelligent Backtracking m Possible m m m Inter. Block Backtracking BT: Chronological Backtracking GBJ: Graph-based Backjumping [Dechter, 1990] GPB: Generalized Partial-Order BT [Bliek, 1998] x. C, y. C x. A, y. A x. B, y. B 1 x. E, y. E 2 y. D 4 x. F, y. F x. J, y. J x. G, y. G x. H, y. H x. I, y. I 3 5
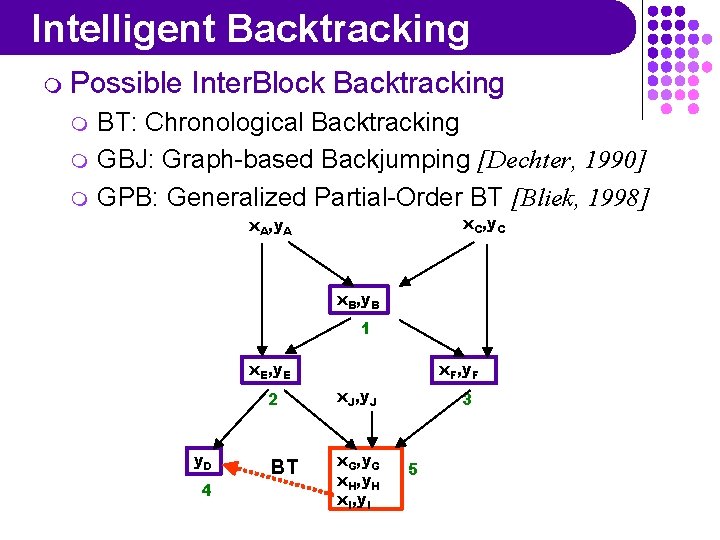
Intelligent Backtracking m Possible m m m Inter. Block Backtracking BT: Chronological Backtracking GBJ: Graph-based Backjumping [Dechter, 1990] GPB: Generalized Partial-Order BT [Bliek, 1998] x. C, y. C x. A, y. A x. B, y. B 1 x. E, y. E y. D 4 x. F, y. F 2 x. J, y. J BT x. G, y. G x. H, y. H x. I, y. I 3 5
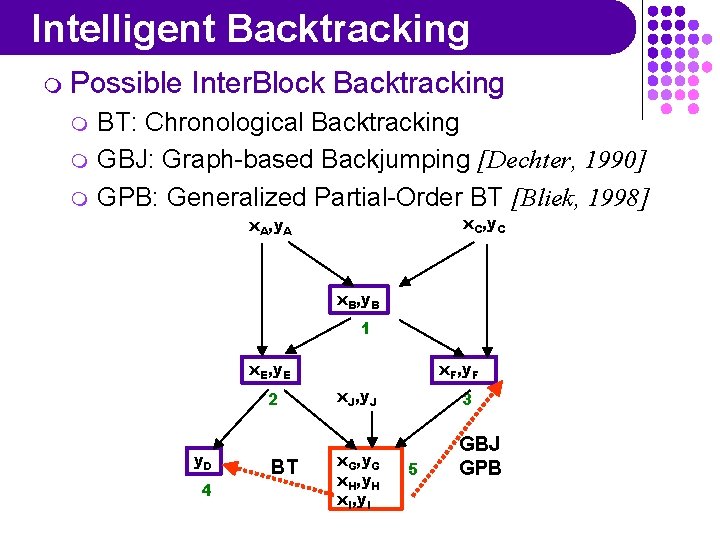
Intelligent Backtracking m Possible m m m Inter. Block Backtracking BT: Chronological Backtracking GBJ: Graph-based Backjumping [Dechter, 1990] GPB: Generalized Partial-Order BT [Bliek, 1998] x. C, y. C x. A, y. A x. B, y. B 1 x. E, y. E 2 y. D 4 BT x. F, y. F x. J, y. J x. G, y. G x. H, y. H x. I, y. I 3 5 GBJ GPB
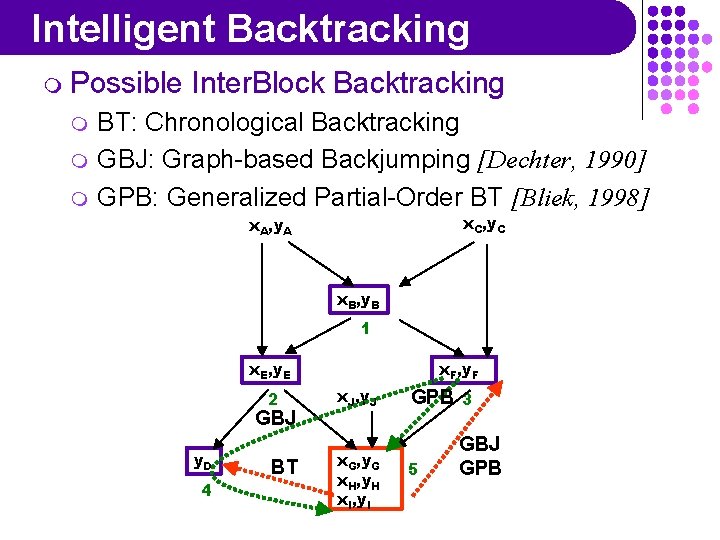
Intelligent Backtracking m Possible m m m Inter. Block Backtracking BT: Chronological Backtracking GBJ: Graph-based Backjumping [Dechter, 1990] GPB: Generalized Partial-Order BT [Bliek, 1998] x. C, y. C x. A, y. A x. B, y. B 1 x. E, y. E 2 GBJ y. D 4 BT x. F, y. F x. J, y. J x. G, y. G x. H, y. H x. I, y. I GPB 3 5 GBJ GPB
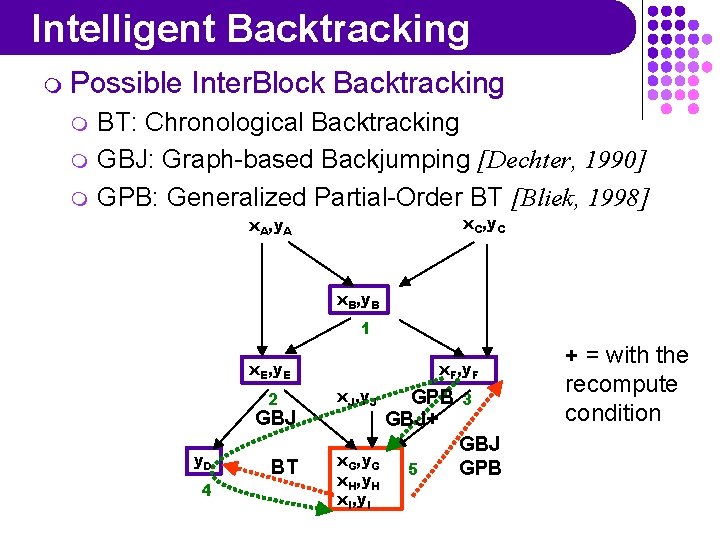
Intelligent Backtracking m Possible m m m Inter. Block Backtracking BT: Chronological Backtracking GBJ: Graph-based Backjumping [Dechter, 1990] GPB: Generalized Partial-Order BT [Bliek, 1998] x. C, y. C x. A, y. A x. B, y. B 1 x. E, y. E 2 GBJ y. D 4 BT x. F, y. F x. J, y. J x. G, y. G x. H, y. H x. I, y. I GPB GBJ+ 5 3 GBJ GPB + = with the recompute condition

IBB: extending the framework m Specific m m treatments as add-ons: Generally, depending on the solving methods Choose the strategy of application (before/after/during a block solving, …) m E. g. : m m Pre-conditioners, Propagators, Inequalities checkers, …
Outline m IBB: a general framework for solving decomposed NCSPs m m m Principle Inputs Process m IBB+Interval: m m m an instance of IBB Interval solving Interblock Filtering Experiments m Conclusion & Future directions

IBB + Interval m Solving method = Interval constraint programming techniques m Backtracking: BT, GBJ & GPB => 3 instances in fact m An interesting add-on: Inter-Block Filtering (IBF) m Propagates domain reductions in following blocks
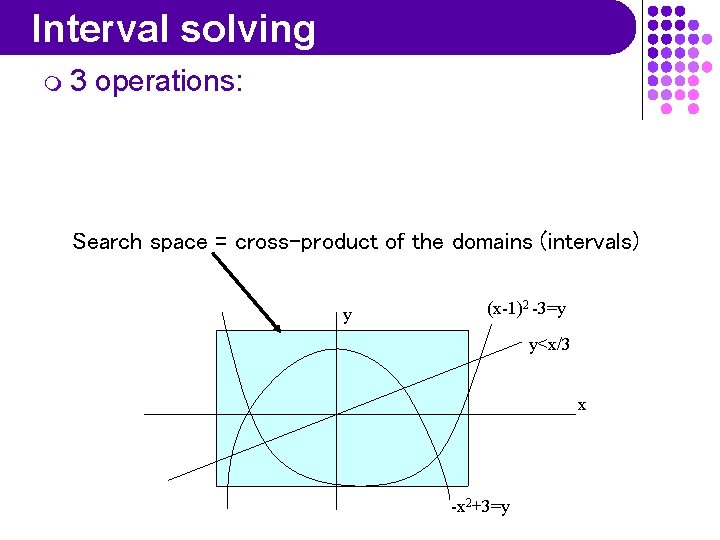
Interval solving m 3 operations: Search space = cross-product of the domains (intervals) y (x-1)2 -3=y y<x/3 x -x 2+3=y
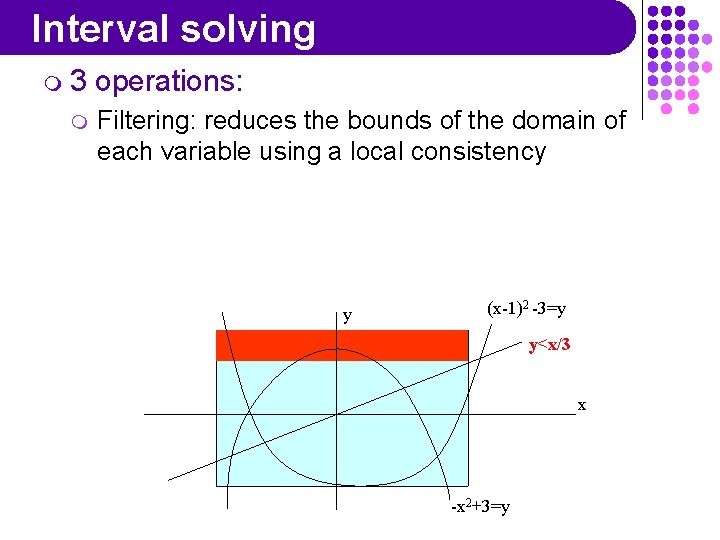
Interval solving m 3 m operations: Filtering: reduces the bounds of the domain of each variable using a local consistency y (x-1)2 -3=y y<x/3 x -x 2+3=y
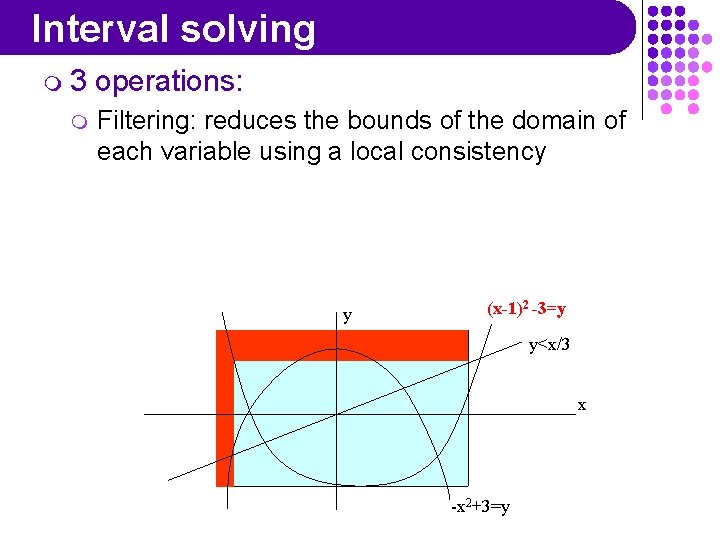
Interval solving m 3 m operations: Filtering: reduces the bounds of the domain of each variable using a local consistency y (x-1)2 -3=y y<x/3 x -x 2+3=y
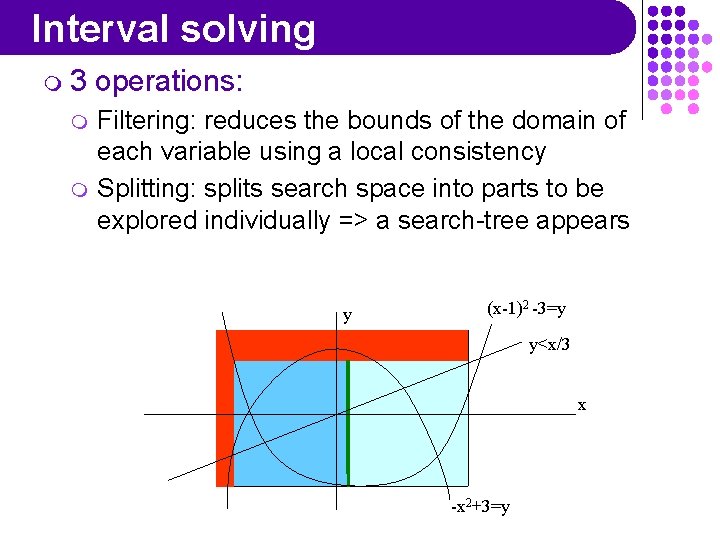
Interval solving m 3 m m operations: Filtering: reduces the bounds of the domain of each variable using a local consistency Splitting: splits search space into parts to be explored individually => a search-tree appears y (x-1)2 -3=y y<x/3 x -x 2+3=y

Interval solving m 3 m m m operations: Filtering: reduces the bounds of the domain of each variable using a local consistency Splitting: splits search space into parts to be explored individually => a search-tree appears Existence: checks if a unique solution exists in the current sub-search-space 2 y (x-1) -3=y y<x/3 x -x 2+3=y
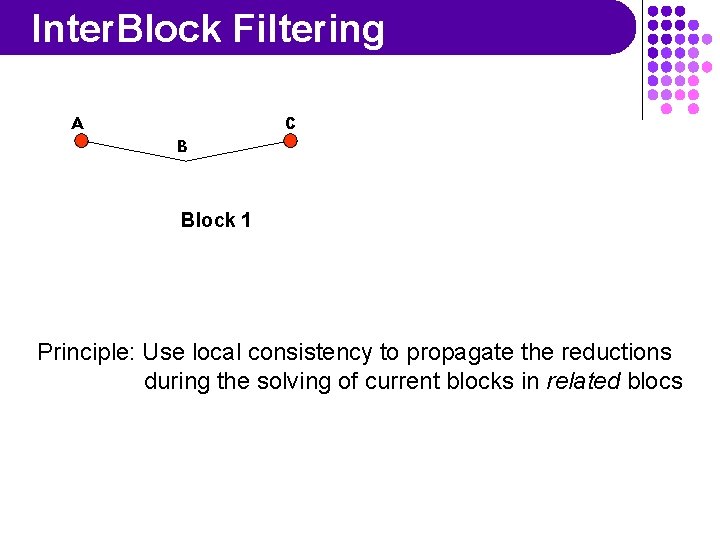
Inter. Block Filtering A C B Block 1 Principle: Use local consistency to propagate the reductions during the solving of current blocks in related blocs
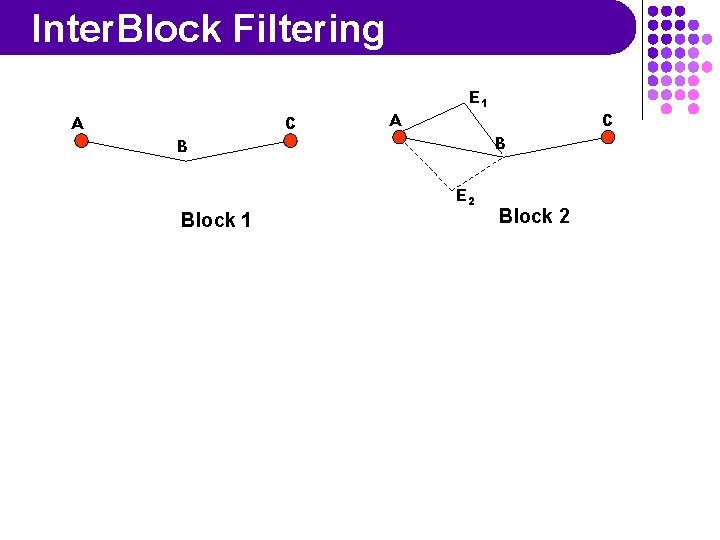
Inter. Block Filtering A C A E 1 B B E 2 Block 1 C Block 2
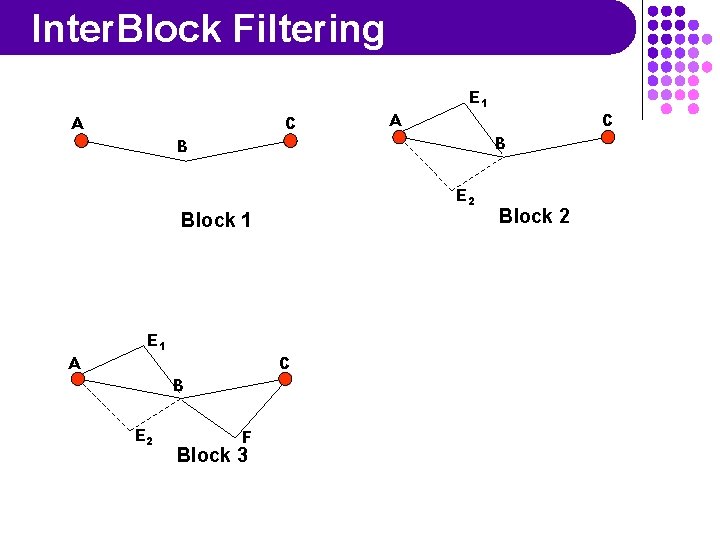
Inter. Block Filtering A C A E 1 B B E 2 Block 1 A E 1 C B E 2 F Block 3 C Block 2
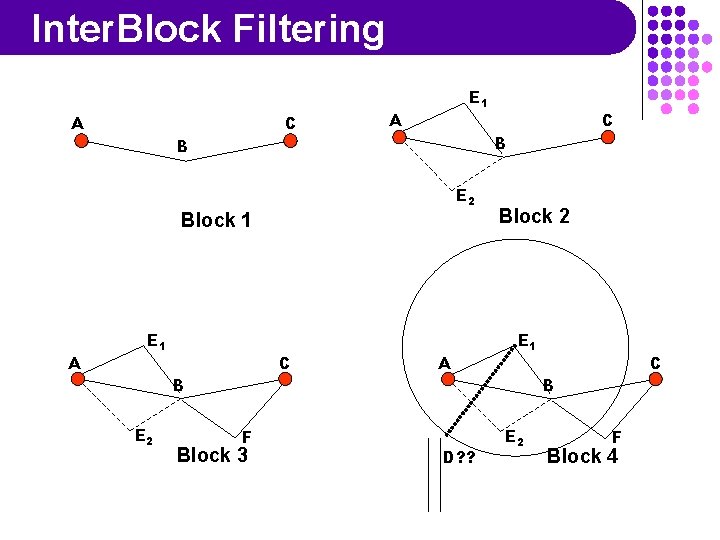
Inter. Block Filtering A C E 1 A B B E 2 Block 1 A E 1 C B E 2 F Block 3 C A D? ? Block 2 E 1 C B E 2 F Block 4
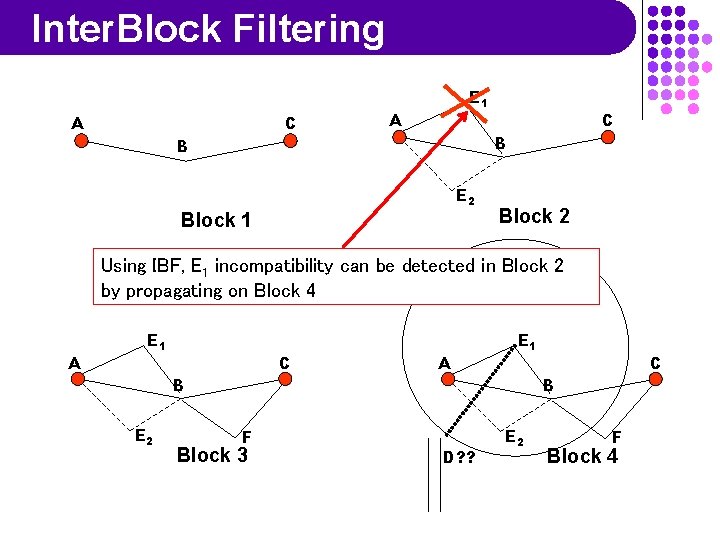
Inter. Block Filtering A C E 1 A C B B E 2 Block 1 Block 2 Using IBF, E 1 incompatibility can be detected in Block 2 by propagating on Block 4 A E 1 C B E 2 F Block 3 A D? ? E 1 C B E 2 F Block 4

Benchmarking m Implemented as a C++ prototype m Run on a PIII 935 m Experimental protocol: m Parameters: ~12 instances of IBB+Interval m Interval Solving: (uses ILOG Solver 5. 0) m m m Filtering: 2 B, 3 B, Box, Bound, 2 B+Box, 3 B+Bound; best choice per problem (usually 2 B+Box or 3 B) Splitting: classical interval bisection Existence: always and only with Box and Bound Backtracking: BT, GBJ, GPB, with or without + Inter. Block Filtering: with or without Inputs: m m NCSPs: 8 from CAD, 4 domain sizes Decomposition: best among 4 methods
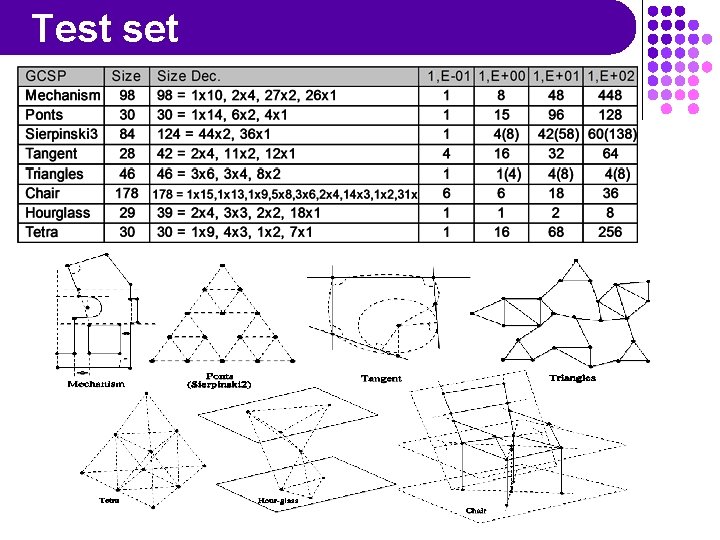
Test set
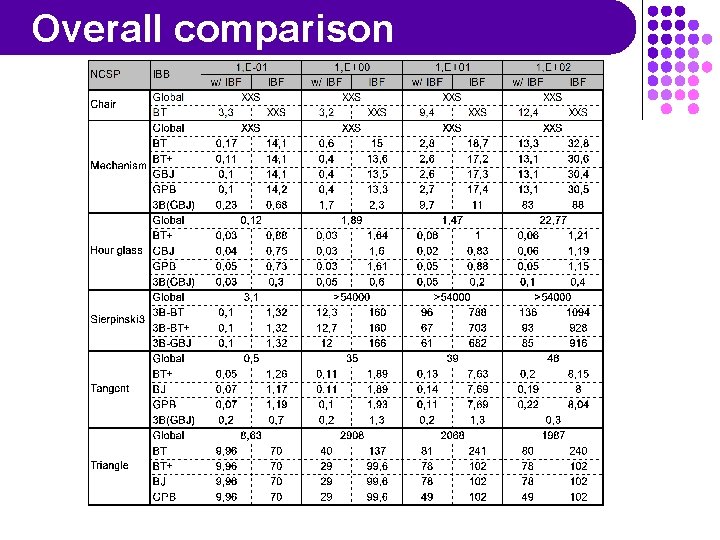
Overall comparison
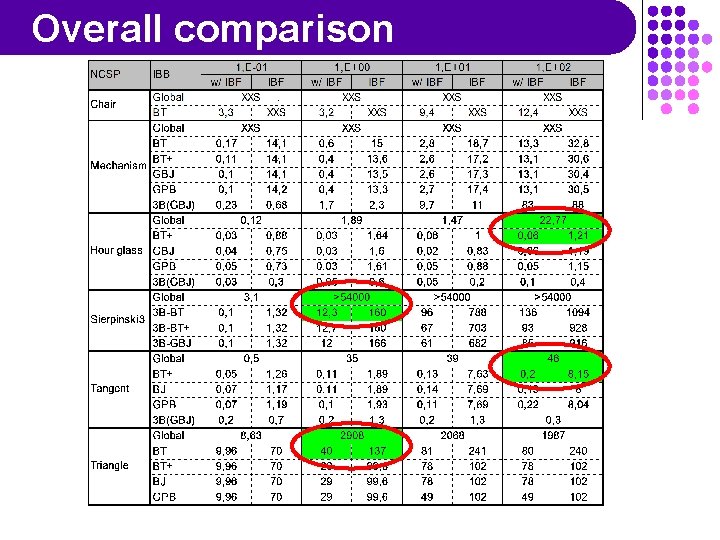
Overall comparison
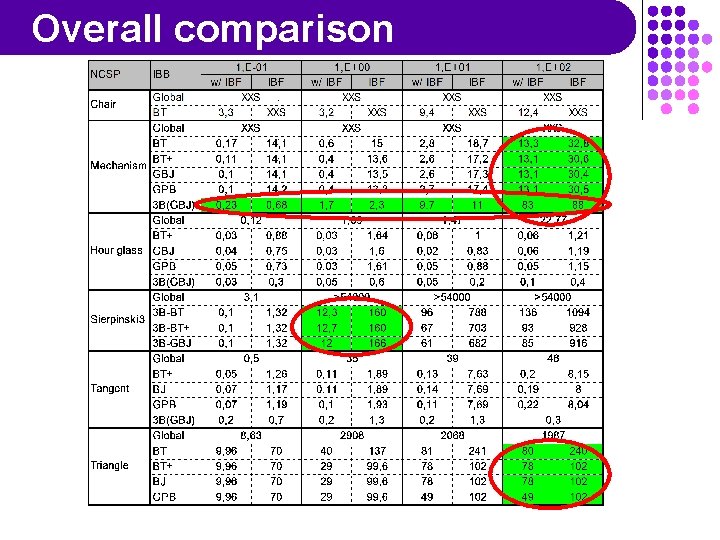
Overall comparison
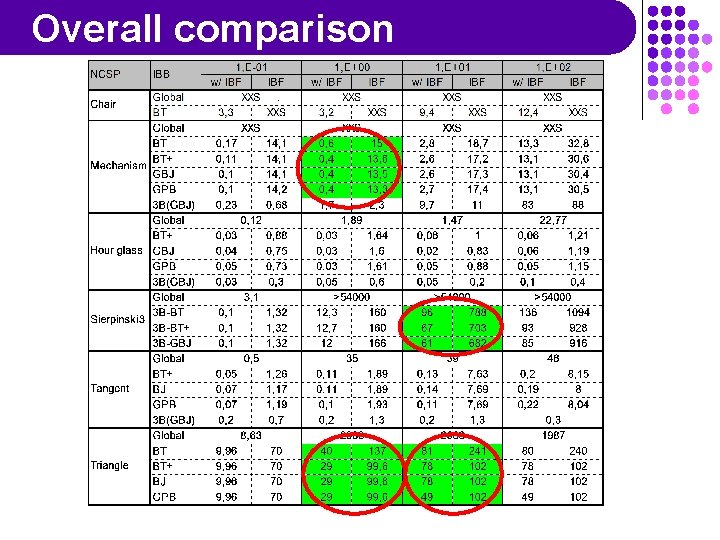
Overall comparison

Outline m IBB: a general framework for solving decomposed NCSPs m m m Principle Inputs Process m IBB+Interval: m m m an instance of IBB Interval solving Interblock Filtering Experiments m Conclusion & Future directions

Conclusion m We have presented a general framework for solving decomposed NCSPs m Instanciating the framework = choosing a BT process, a set of solving methods, and optionally a set of add-ons m From m the experiments, we can say that: Decomposition seems very interesting for NCSPs with a structure Filtering, a strength of constraint programming, seems counter-productive when used against the structure Intelligent BT seems more profitable, and introduces at least no overhead

Future directions m Try other instances of IBB, involving different solvers m m Intervals + symbolic … m Solver m dynamic selection strategies According to blocks’ properties that may change (block = parametric NCSP) m Use other frameworks to solve decomposed NCSPs m m m Multi-agent systems Solver cooperation frameworks …
- Slides: 55