IntensityModulated Radiotherapy and Inverse Planning CM Charlie Ma

Intensity-Modulated Radiotherapy and Inverse Planning C-M Charlie Ma, Ph. D. Department of Radiation Oncology Fox Chase Cancer Center Philadelphia, PA 19111, USA

Outline · Rationale for intensity-modulated radiotherapy · The IMRT process · Elements of an inverse planning system · Concepts of inverse planning · Inverse planning algorithms

Clinical Rationale for IMRT l To improve local-regional control through dose escalation to improve overall survival l To reduce normal tissue complications to improve quality of life l To reduce treatment time/cost

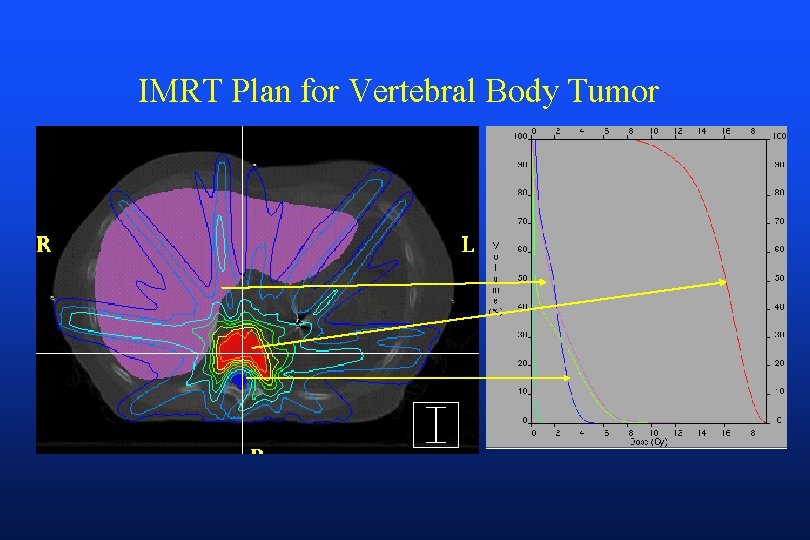
IMRT Plan for Vertebral Body Tumor

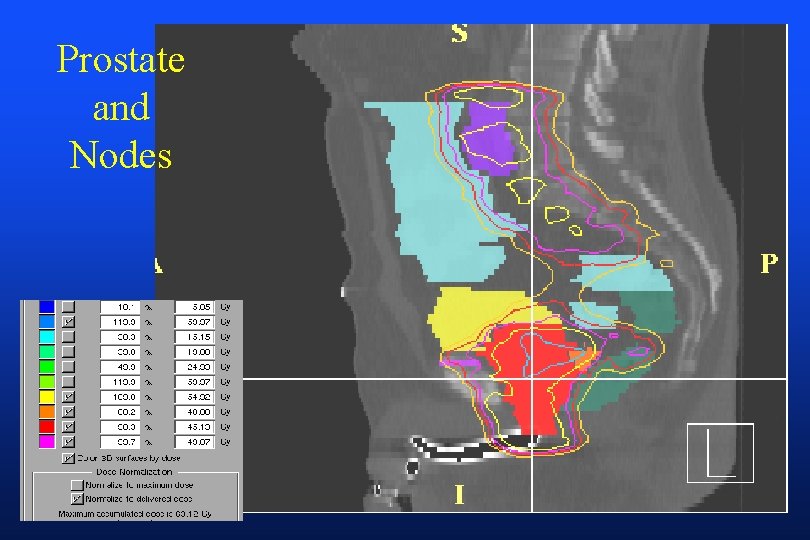
Prostate and Nodes

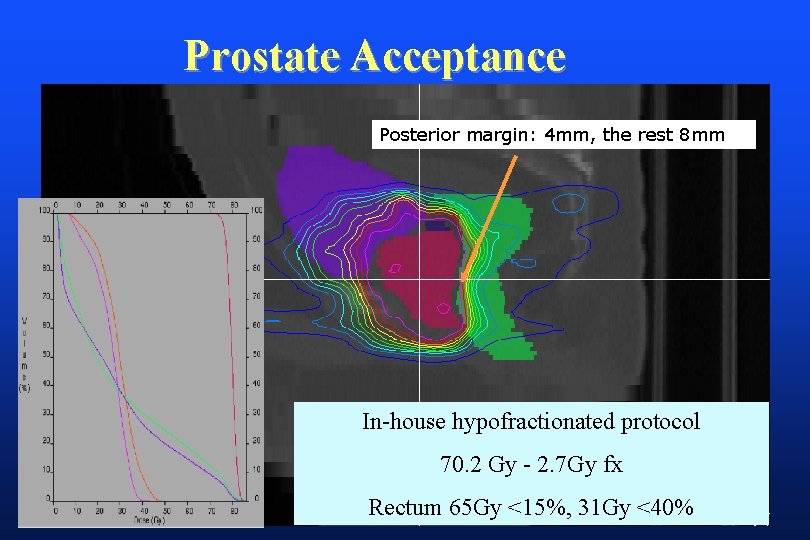
Prostate Acceptance Posterior margin: 4 mm, the rest 8 mm In-house hypofractionated protocol 70. 2 Gy - 2. 7 Gy fx Rectum 65 Gy <15%, 31 Gy <40%

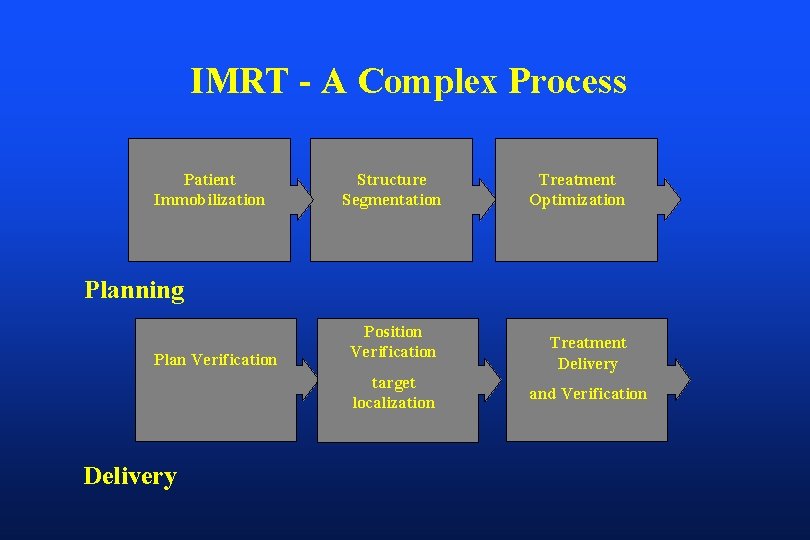
IMRT - A Complex Process Patient Immobilization Structure Segmentation Treatment Optimization Planning Plan Verification Position Verification target localization Delivery Treatment Delivery and Verification

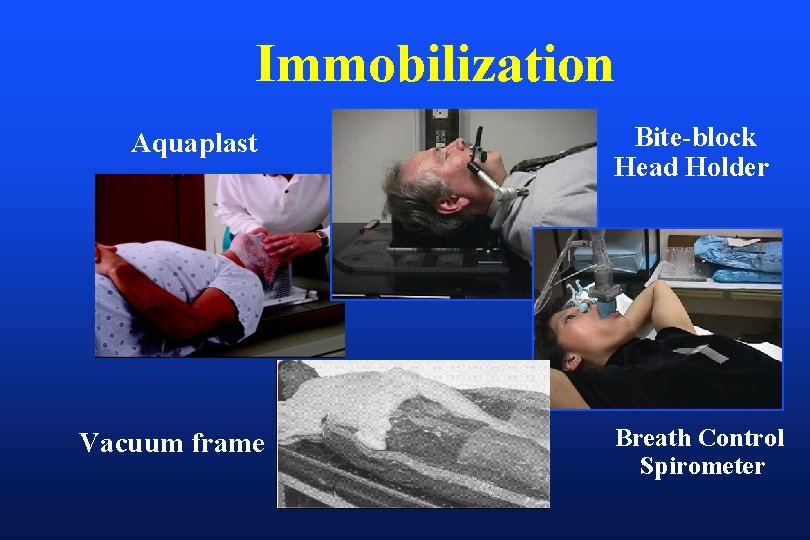
Immobilization Aquaplast Vacuum frame Bite-block Head Holder Breath Control Spirometer

CT/MRI/PET Image Acquisition

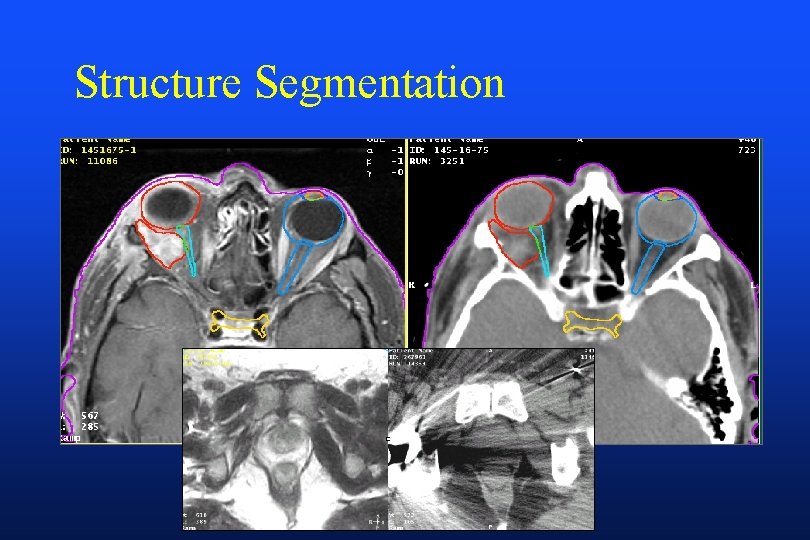
Structure Segmentation

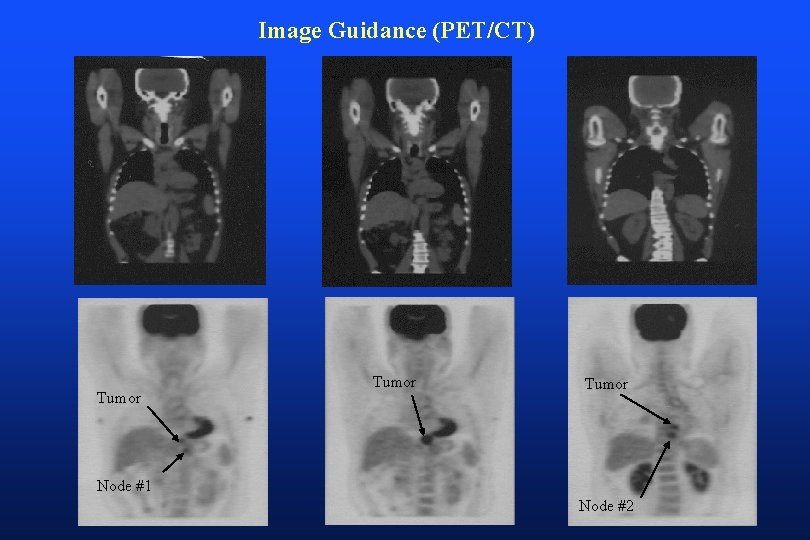
Image Guidance (PET/CT) Tumor Node #1 Node #2

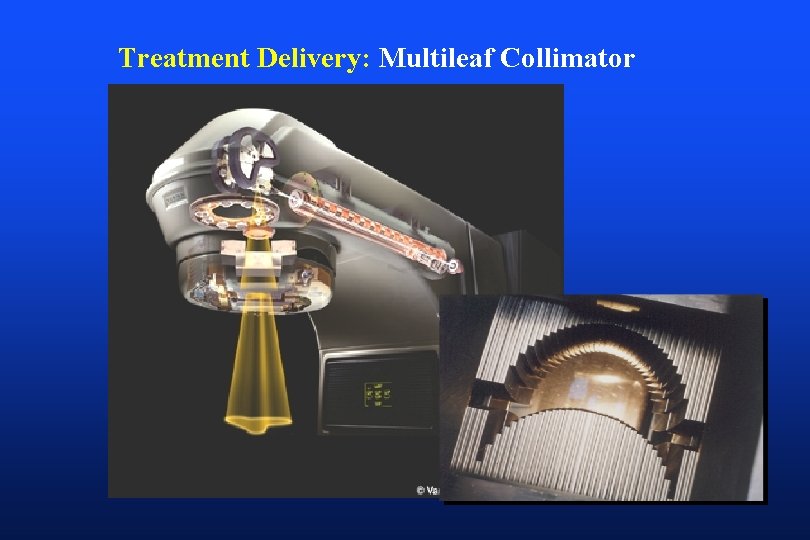
Treatment Delivery: Multileaf Collimator

Beam Delivery with a MLC

Beam Delivery with a MLC 0. 03 MU Dose Delivery 2. 5 mm spatial longitudinal 5. 0 mm spatial lateral

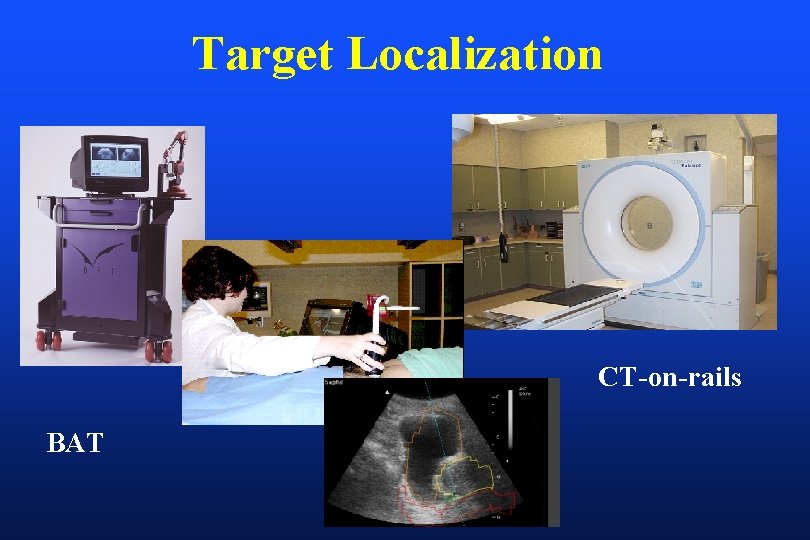
Target Localization CT-on-rails BAT

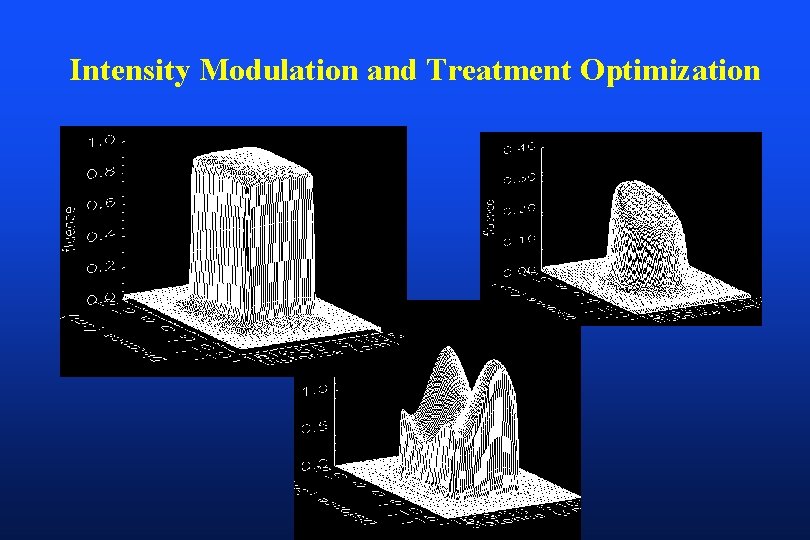
Intensity Modulation and Treatment Optimization

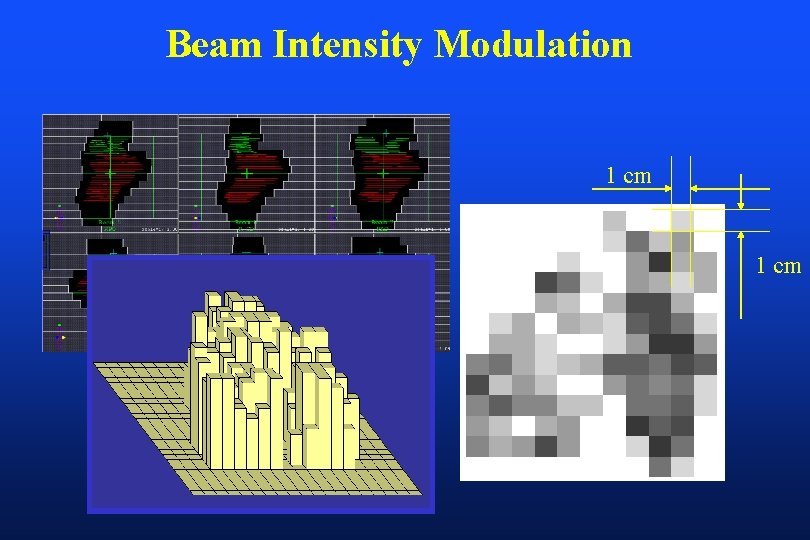
Beam Intensity Modulation 1 cm

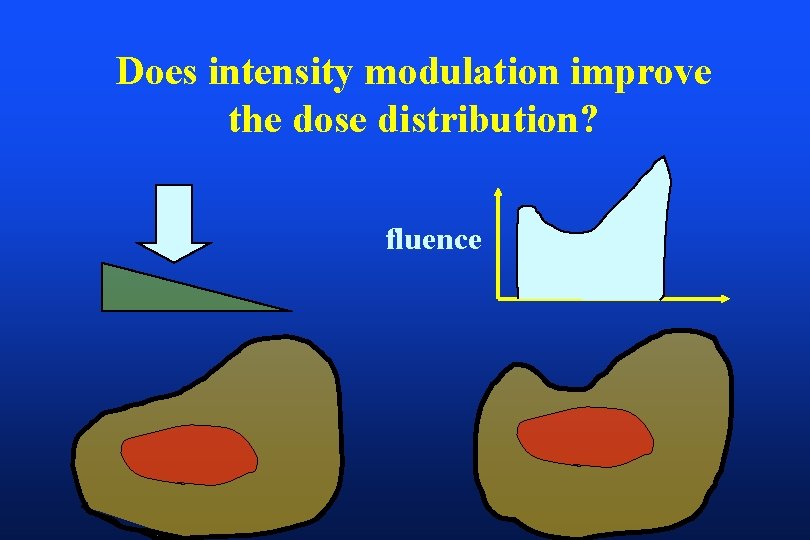
Does intensity modulation improve the dose distribution? fluence

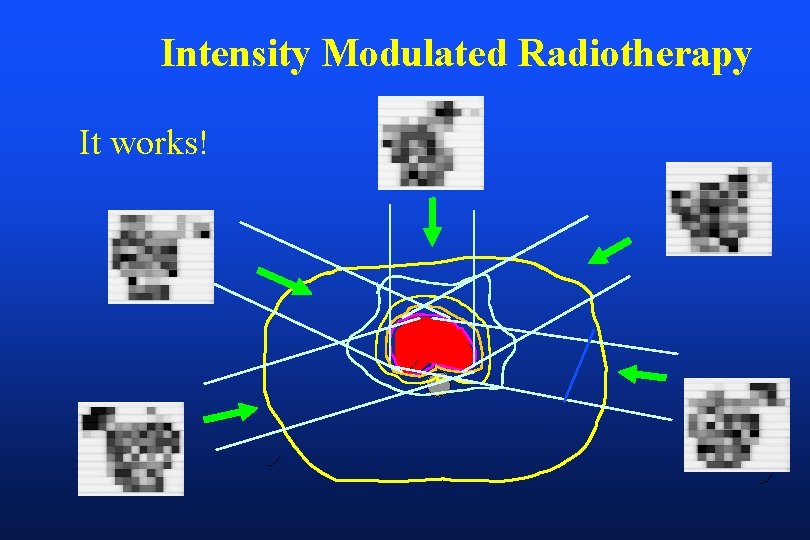
Intensity Modulated Radiotherapy It works!

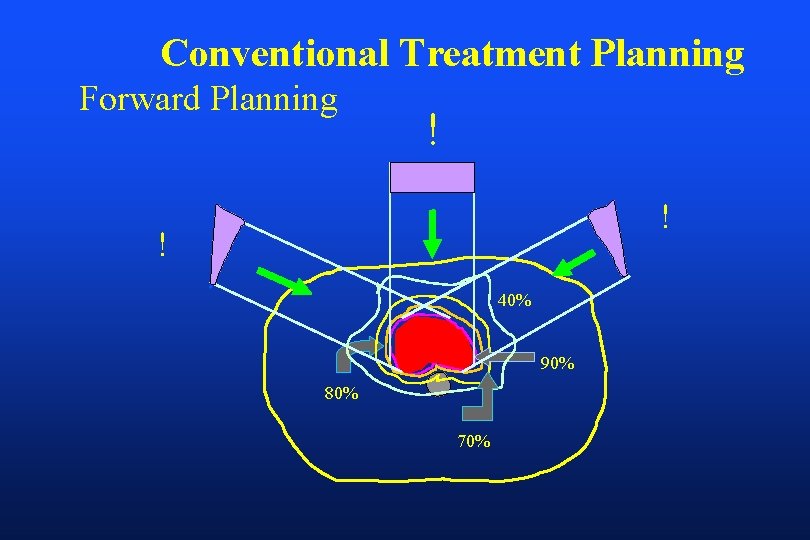
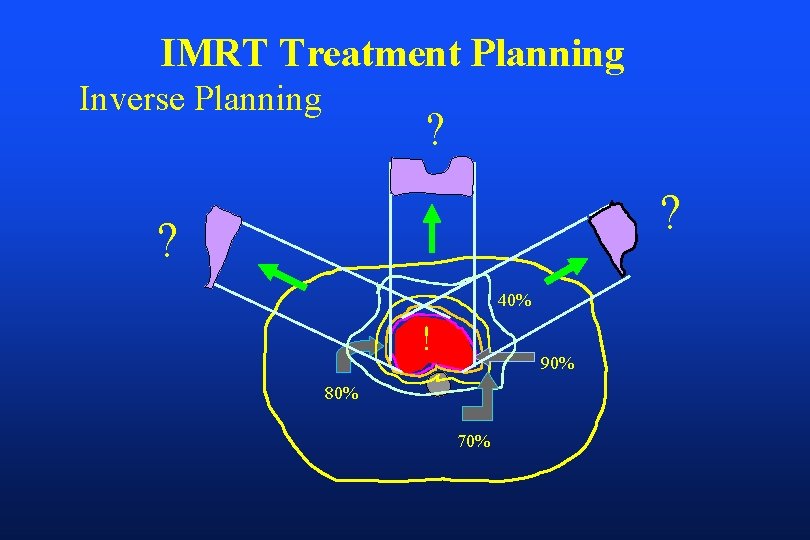
How can we determine the individual beamlet weights for IMRT ? Conventional treatment planning starts with a set of beam weights and obtains a plan by a trial-and-error process. This procedure won’t work for IMRT since there are too many unknowns (>2000 beamlet weights).

Conventional Treatment Planning Forward Planning ! ! ! 40% 90% 80% 70%

IMRT Treatment Planning Inverse Planning ? ? ? 40% ! 90% 80% 70%

What is in an Inverse Planning System? Patient data Dose calculation Optimization Leaf sequencing Interface with R&V

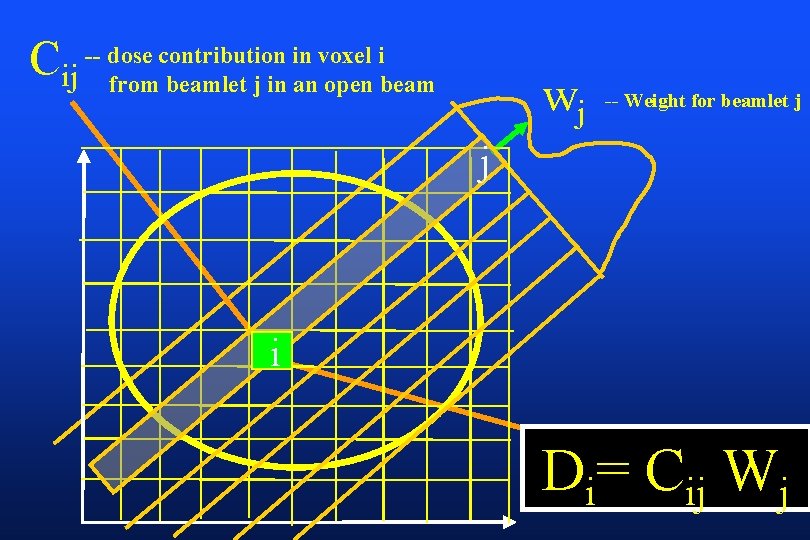
contribution in voxel i Cij -- dose from beamlet j in an open beam wj -- Weight for beamlet j j i Di= Cij Wj

Dose Calculation for IMRT · Total dose in voxel i j i · Or dose in any voxel in a more generic form

What’s Inverse Planning ? · Assume D 0 is the desired dose · and W 0 the required beamlet weights and we have

is an exact mathematical expression of inversely derived beamlet weights for a desired dose distribution D 0 However, Unfortunately this inverse process does not work in most, if not all, realistic treatment cases. Practically, what we want is a set of beamlet weights that will give us the best available dose distribution !

What’s Our Solution ? · Assume D 0 is the desired dose and W 0 the required beamlet weights Ideal but may be a pie in the sky! · What we want is to derive Db the “best achievable” dose and Wb the corresponding beamlet weights Not ideal but achievable The question is how do we know Db is good enough compared with D 0?

What’s an Objective Function ? • An objective function is a mathematical evaluation of a treatment dose distribution (wrt. the desired dose distribution). • Ideally, it should include all of our knowledge of radiotherapy: physical as well as biological dosimetric requirements. • The question now is how to “optimize” a given objective function.

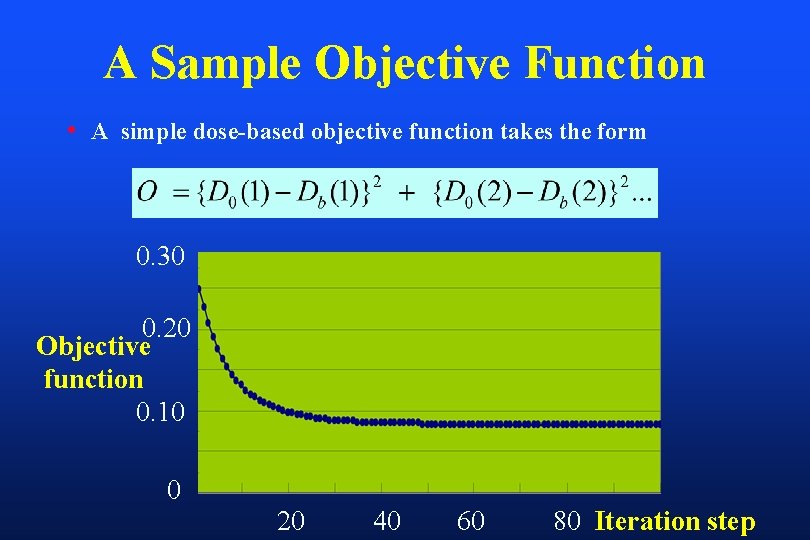
A Sample Objective Function • A simple dose-based objective function takes the form 0. 30 0. 20 Objective function 0. 10 0 20 40 60 80 Iteration step

There are many ways to build an objective function (everybody wants his/her own)! There are many ways to optimize a treatment plan for a given objective function (forward, backward, hybrid, etc)! An inverse planning system may use any optimization algorithms (more likely it is a forward planning, or a hybrid, process).

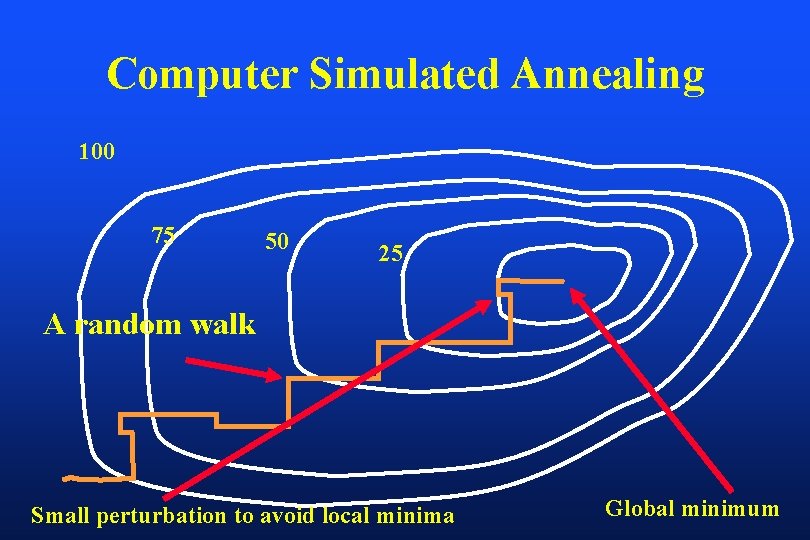
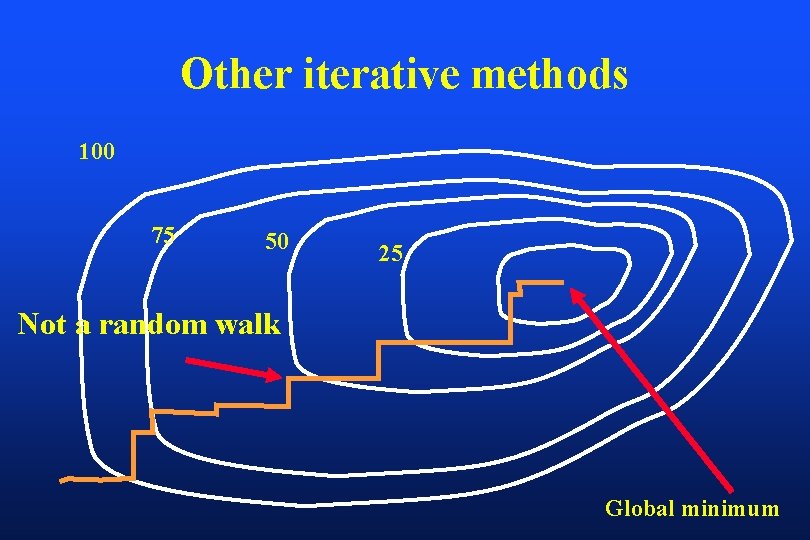
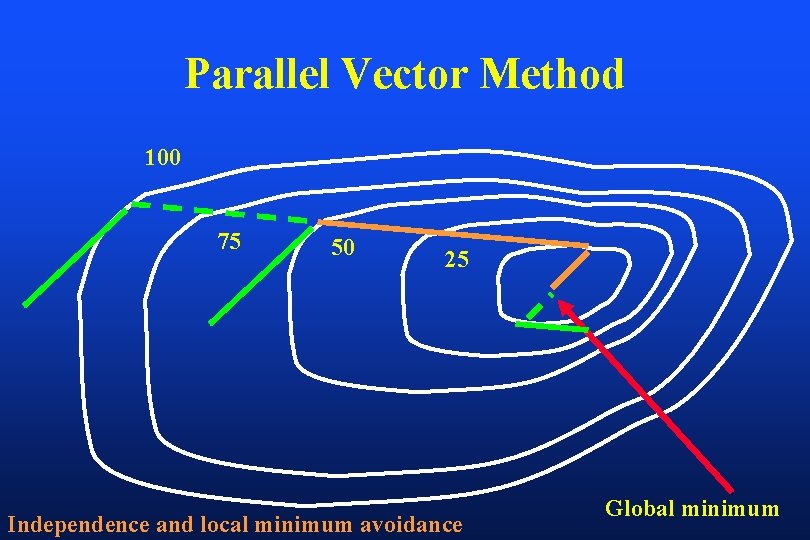
Optimization of a Multi-Dimensional Objective Function Computer simulated annealing (Corvus) Gradient method (Helios, Pinnacle) Filtered back-projection (Konrad) Other iterative methods (CMS) Parallel vector method (? )

Most optimization methods use an iterative approach, one way or another Major differences between optimization systems are the construction of the objective function and the methods for search directions and step-length

Computer Simulated Annealing 100 75 50 25 A random walk Small perturbation to avoid local minima Global minimum

Other iterative methods 100 75 50 25 Not a random walk Global minimum

Gradient Method 100 75 50 25 local downhill gradient [ -grad f(w )] Global minimum

Parallel Vector Method 100 75 50 25 Independence and local minimum avoidance Global minimum

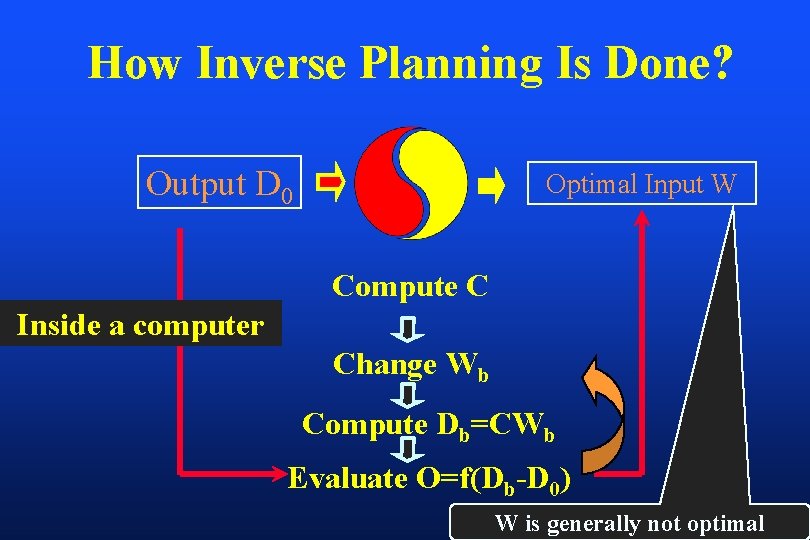
How Inverse Planning Is Done? Output D 0 Optimal Input W Compute C Inside a computer Change Wb Compute Db=CWb Evaluate O=f(Db-D 0) W is generally not optimal

Factors Affecting Optimization Results · Number of beams · Beam orientation · Optimization parameter and dose constraints · Optimization algorithm and objective function · Experience is gold!

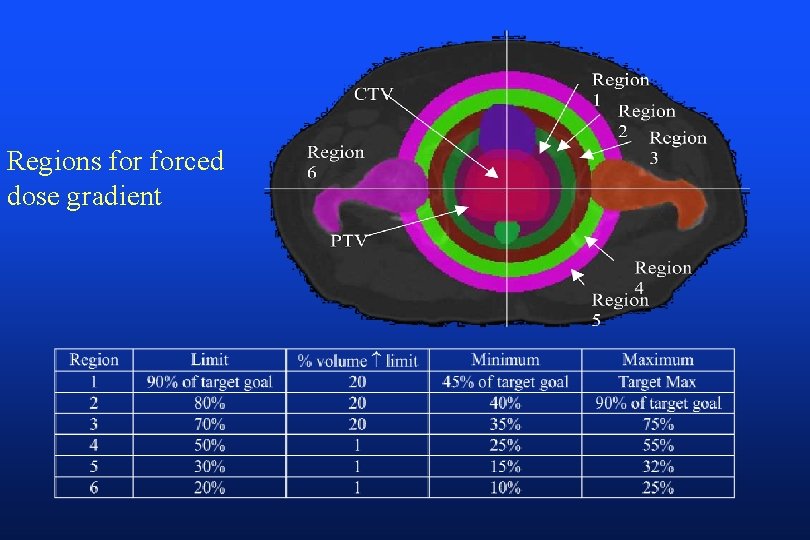
Regions forced dose gradient

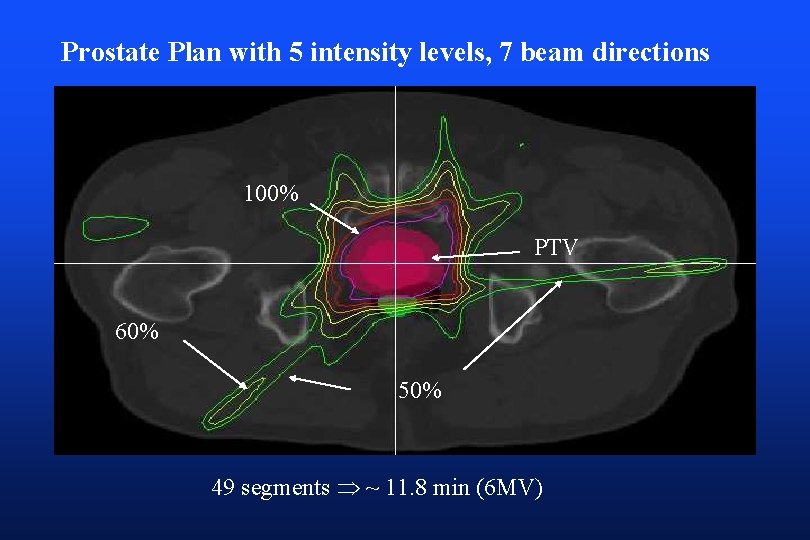
Prostate Plan with 5 intensity levels, 7 beam directions 100% PTV 60% 50% 49 segments ~ 11. 8 min (6 MV)

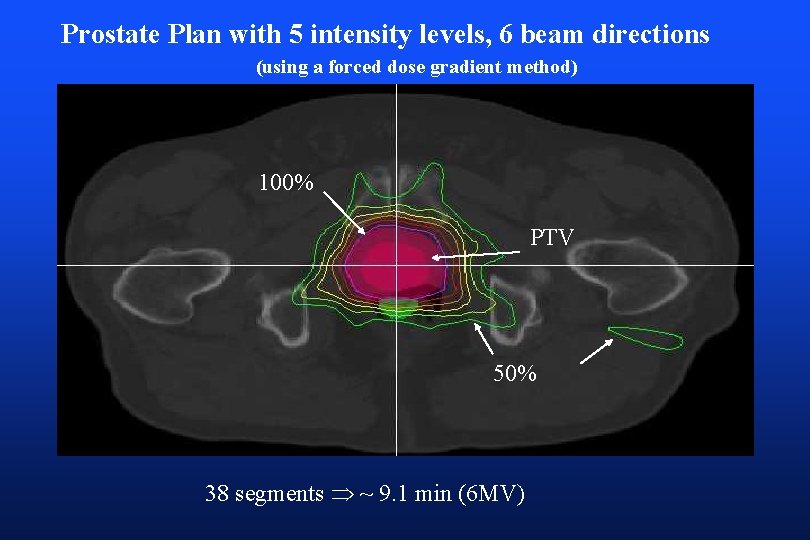
Prostate Plan with 5 intensity levels, 6 beam directions (using a forced dose gradient method) 100% PTV 50% 38 segments ~ 9. 1 min (6 MV)

Conclusions · An inverse planning system does not give an optimal plan, but a customized plan · Inverse planning generally works but it is not magic! · It works better for you if you know how it works

Conclusions (cont. ) · If it does not work, it’s more likely due to the complexity of the situation…

Conclusions (cont. ) · If it does not work, maybe the situation is too simple. . .

Conclusions (cont. ) · Fortunately, we are very familiar with the situation and we also learn from each other. Therefore, we reach more or less the same goal. . .

Conclusions (cont. ) · Treatment optimization is an integral part of IMRT · Much more work is needed for the clinical implementation of IMRT · Much more effort is needed to keep it running smoothly and keep pace with upgrades and future enhancements

Thank You