Intelligent Practice EMBEDDING INTELLIGENT PRACTICE INTO EVERY DAY

Intelligent Practice EMBEDDING INTELLIGENT PRACTICE INTO EVERY DAY TEACHING. Jonathan Hall: Lead Practitioner School: Leeds City Academy Twitter: @Study. Maths Website: Maths. Bot. com

Some of my resources

Recent Updates mathsbot. com/#Manipulatives

Workshop Aims Outline three types of practice; ‘SLOP’, ‘Purposeful’ and ‘Intelligent’ and when to use them with our students. Signpost resources to support all types of practice. Take a look at how well-designed ‘Intelligent’ practices can steer pupils away from mechanical processes and encourage them to think about the structure of the maths. An opportunity for you to develop some intelligent practice questions of your own.

Types of practice S. L. O. P Purposeful Intelligent

S. L. O. P (S)hed (L)oads (O)f (P)ractice “Don’t practice until you get it right, practice until you can’t get it wrong. ”

Maths. Bot. com Maths. Bot – Differentiated questions Maths. Bot – Starter generator

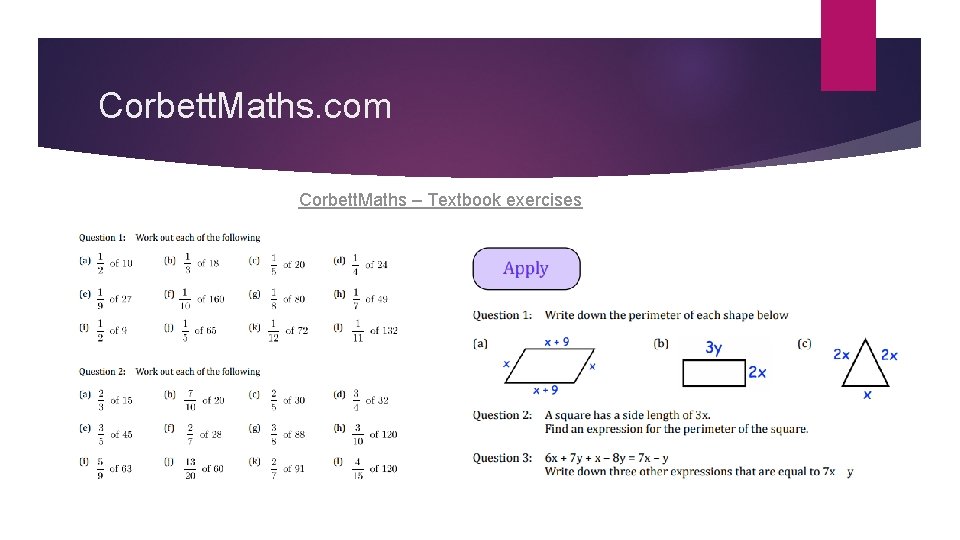
Corbett. Maths. com Corbett. Maths – Textbook exercises

taylorda 01. weebly. com Dave Taylor - Increasingly difficult questions

S. L. O. P. in 1955

S. L. O. P – Other sources of resources? Any other S. L. O. P resources? Write them on a post-it.

Purposeful Practice “Demands focus and intense concentration on a skill or problem beyond the ordinary. ”

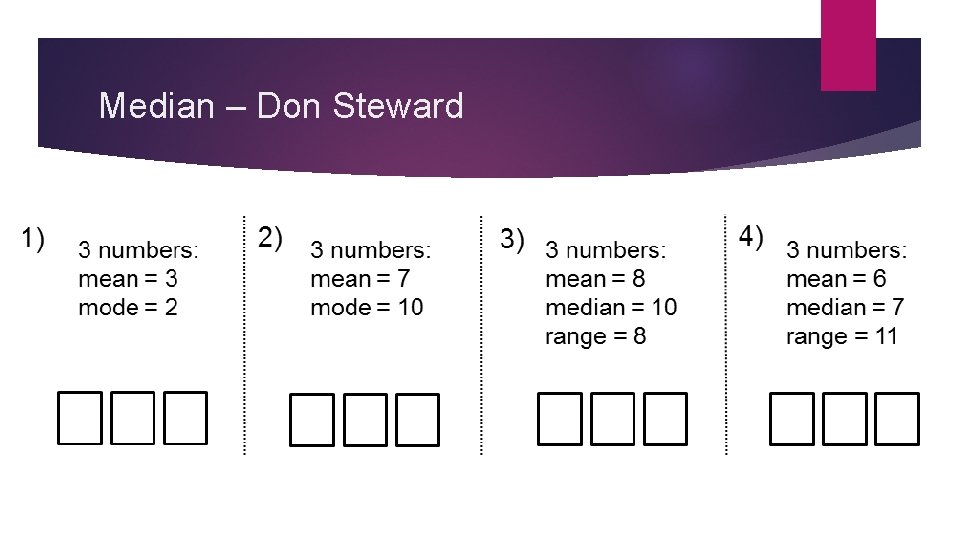
Median – Don Steward

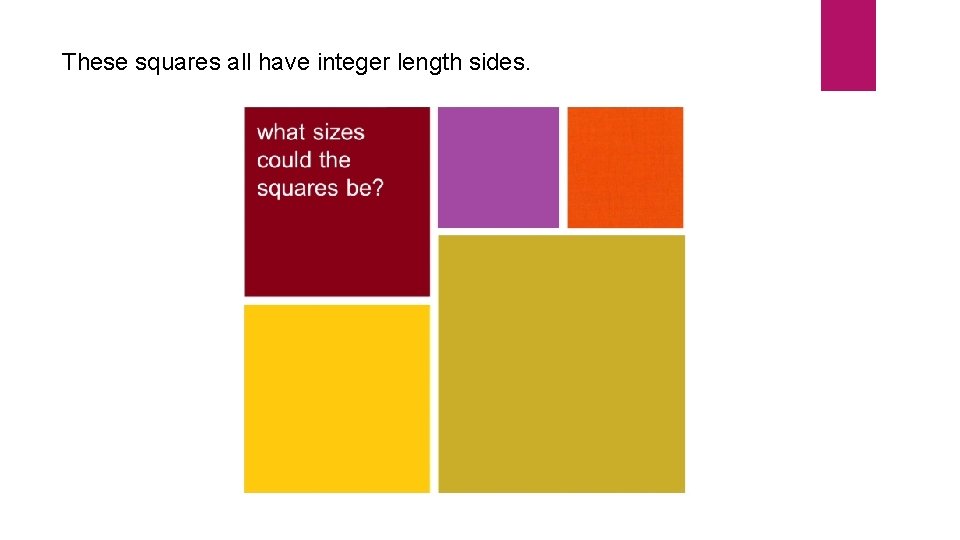
These squares all have integer length sides.

Starting Points @Chris. Mc. Grane 84 startingpointsmaths. blogspot. com

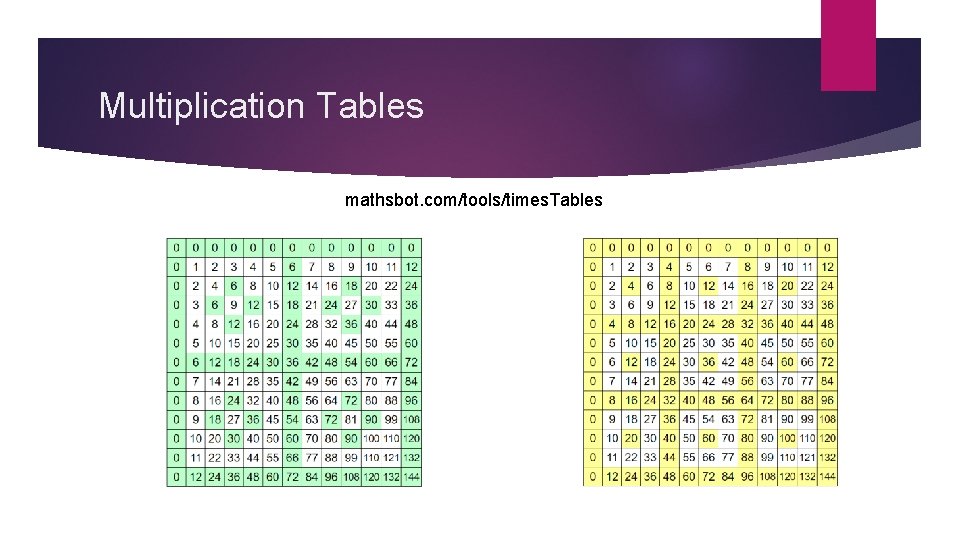
Multiplication Tables mathsbot. com/tools/times. Tables

PP – Other sources of resources? Any other purposeful practice resources? Write them on a post-it.

What is Intelligent Practice? A key feature of teaching for mastery is the precise designing of pupil activities and practice questions, so that, rather than pupils repeating a mechanical activity, they are taken down a path where thinking process is practised with increasing creativity. Through connected calculations, the pupil has the opportunity to think about key concepts. The arrangement of these tasks and exercises draw pupils’ attention to patterns, structure and mathematical relationships, thus providing ‘intelligent practice’ and the opportunity to deepen conceptual understanding. “Memory is the residue of thought” Daniel Willingham

An ‘Intelligent’ sequence @Mr. Mattock § 2 × 3 + 5 × 3 § 2 × 7 + 5 × 7 § 2 × 12 + 5 × 12 § 2 × 1000 + 5 × 1000 § 2 × 1 million + 5 × 1 million

Fractions I expect the answer to be…because… Encourage vigorous use of correct mathematical language

Collecting Like Terms § 2 × 3 + 5 × 3 § 2(x + 1) + 5(x + 1) § 2 × n + 5 × n § 2(x + 1) + 5(1 + x) § 2 n + 5 n § 2(x + 1) + 5(x - 1) § 2 n + 5 m § x(x + 1) + 5(x + 1) § 2(n + 1) + 5(n + 1)

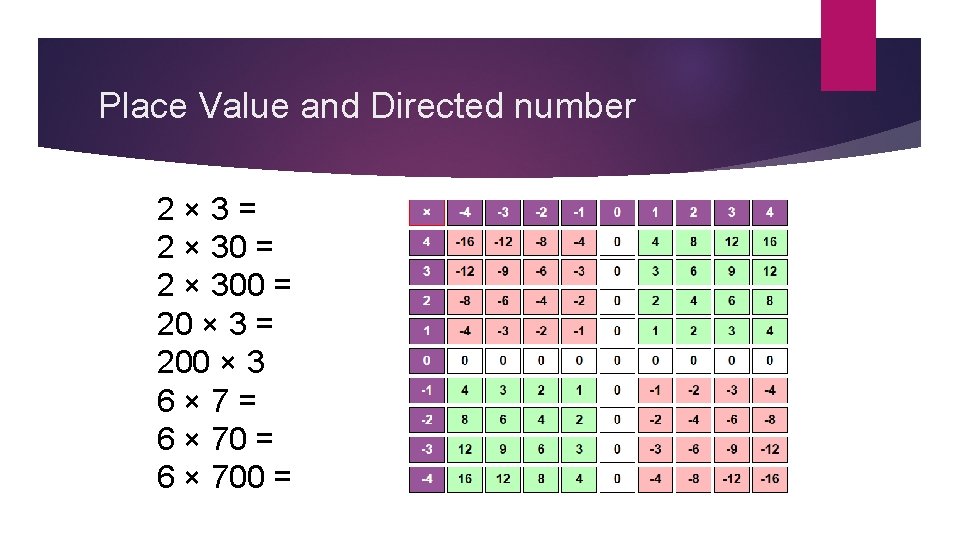
Place Value and Directed number 2 × 3 = 2 × 300 = 20 × 3 = 200 × 3 6 × 7 = 6 × 700 =

Intelligent Practice Useful Websites

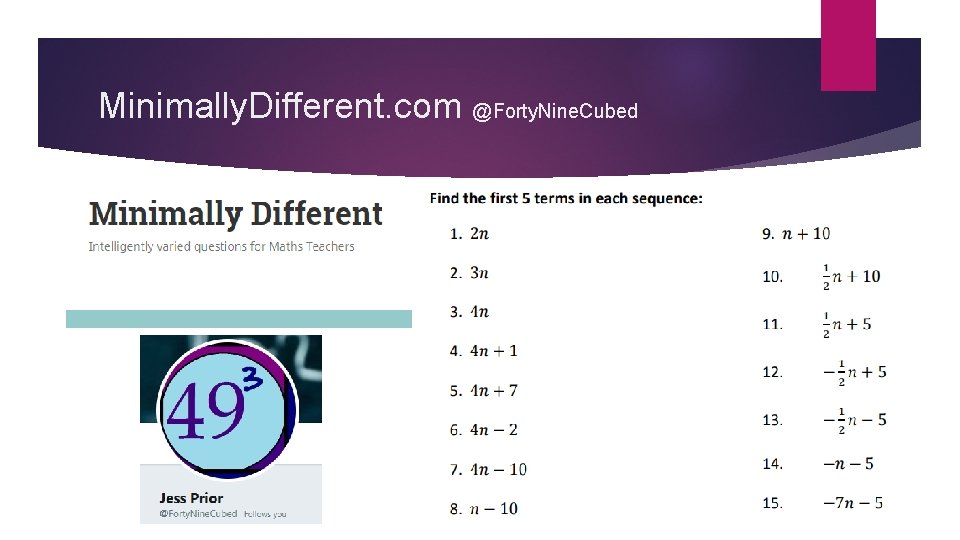
Minimally. Different. com @Forty. Nine. Cubed

Variation. Theory. com

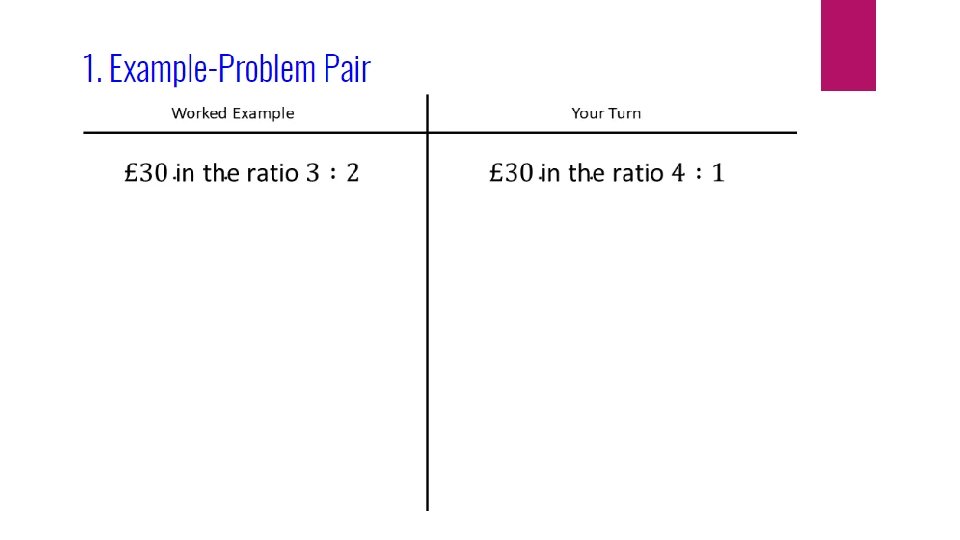
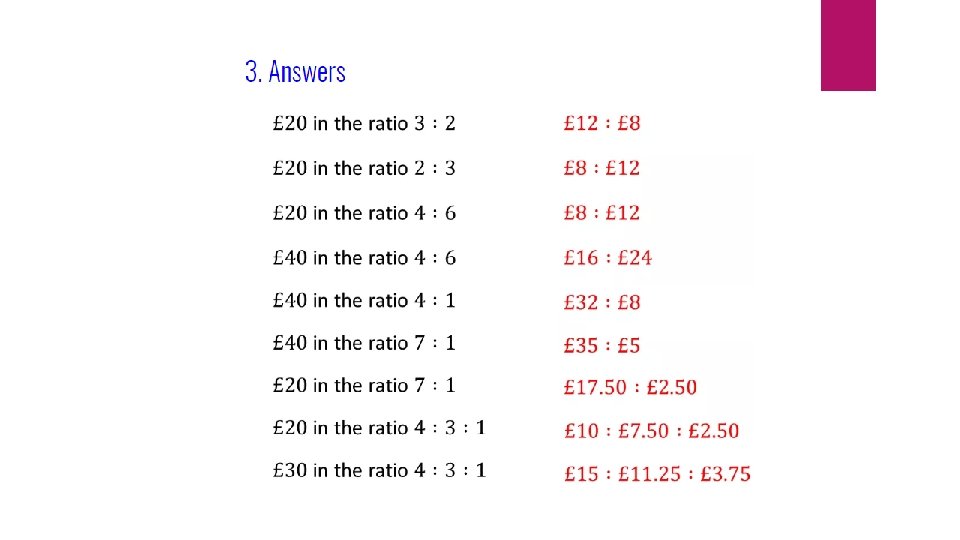
My Turn – Your Turn Linked examples

My Turn – Your Turn A car travel 45 km in 1 hour 15 minutes. A car travel 90 km in 1 hour 15 minutes. Calculate the average speed of the car. A car travel 120 km in 3 hours. A car travel 60 km in 1 hour 30 minutes. Calculate the average speed of the car.

My Turn – Your Turn

My Turn – Your Turn

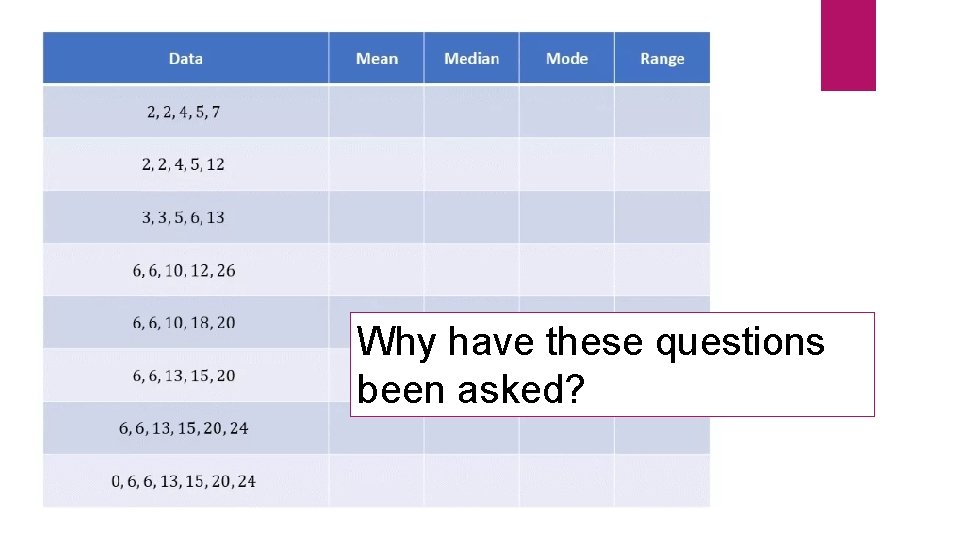
Your Turn Why have these questions been asked?

Intelligent Design Choose a topic you know you will be teaching in the near future. Design a series of questions to ‘intelligently practice’ a topic. As a leader, how will ensure your department is confident in creating, adapting and using intelligent practice effectively? Consider when would be the best time to implement intelligent practice in a learning episode.

Key Takeaways @Mr. Barton. Maths • Choosing examples is possibly the most important part of the planning process. • Carefully designed progression and variation in examples and exercises can allow students to make vital connections that develop both procedural fluency and conceptual understanding. • Non-examples can be an effective way of adding clarity and completeness to students’ understanding of a concept.

Non. Examples. com