INTELLIGENCE ARTIFICIELLE IAR1001 Modlisation de lincertidude et raisonnement

INTELLIGENCE ARTIFICIELLE IAR-1001

• • Modélisation de l’incertidude et raisonnement probabiliste (Réseaux Bayesien) Introduction Probabilité jointe Marginale/Probabilité conditionnelle Chain rule Algorithme de création d’un BN Autre exemple de BN LECTURES: Chapitres 13, 14 Russell & Norvig Notes de cours (site ftp UQTR)

Introduction (Agent) • Agents Utility-Based dans le contexte d’incertidude États incertains Effets des actions incertains Capteurs bruités

Introduction (Théorie probabiliste) • Supposons, qu’un taxi autonome a pour but de déposer un passager à l’aéroport et ce à temps pour son vol. • Un agent utility-based typique pourrait planifier une action du genre, A 90, qui implique de quitter la maison 90 minutes avant le départ du vol tout en conduisant à une vitesse raisonnable, et ce même si l’aéroport est a une distance de 5 miles. • Un taxi agent logique ne sera pas capable de conclure avec certitude que: “Le plan A 90 nous conduit à l’aéroport à temps. ” • Il pourrait déduire une conclusion plus faible du genre: “ Le plan A 90 nous mènera à l’aéroport à temps, si le véhicule ne brise pas ou ne manque pas d’essence, et ne fait pas un accident, et qu’il n’y a pas d’accident sur le pont, et que l’avion ne part pas avant l’heure prévue, et qu’aucun météorite ne frappe le taxi et …. . ” • Aucune de ces conditions ne peut être deduites avec certitude, le succès de ce plan ne peut être inféré.

Introduction (Théorie probabiliste) • La théorie des probabilités permet de modéliser la vraisemblance d’événements, information pouvant être dérivée des croyances/certitudes d’un agent, ou des observations empiriques de ces événements. • Donne un cadre théorique pour mettre à jour la vraisemblance d’événements après l’acquisition d’observations, par exemple, après avoir observé qu’il n’y a pas de trafic, la probabilité que A 90 me permette d’arriver à temps devrait changer comment ? • Facilite la modélisation en permettant de considérer l’influence de phénomènes complexes comme du bruit.

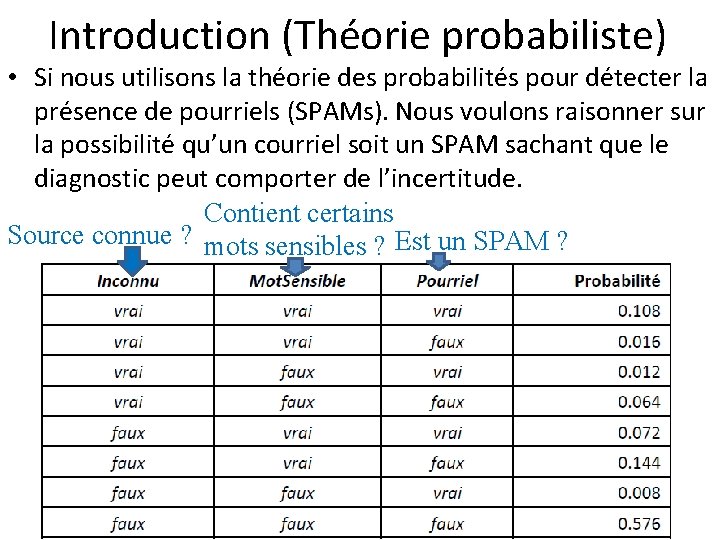
Introduction (Théorie probabiliste) • Si nous utilisons la théorie des probabilités pour détecter la présence de pourriels (SPAMs). Nous voulons raisonner sur la possibilité qu’un courriel soit un SPAM sachant que le diagnostic peut comporter de l’incertitude. Contient certains Source connue ? mots sensibles ? Est un SPAM ?

Introduction (Théorie probabiliste) • Variables aléatoires impliquées: – Inconnu: L’adresse de l’expéditeur est-elle connue ? – Mot. Sensible: Le courriel contient-il des mots contenus dans une liste de mots "sensibles" ? – Pourriel: Le courriel est-il un pourriel ? "la probabilité que Inconnu=vrai et Mot. Sensible=vrai et Pourriel=vrai" La somme de ces probabilités est 1

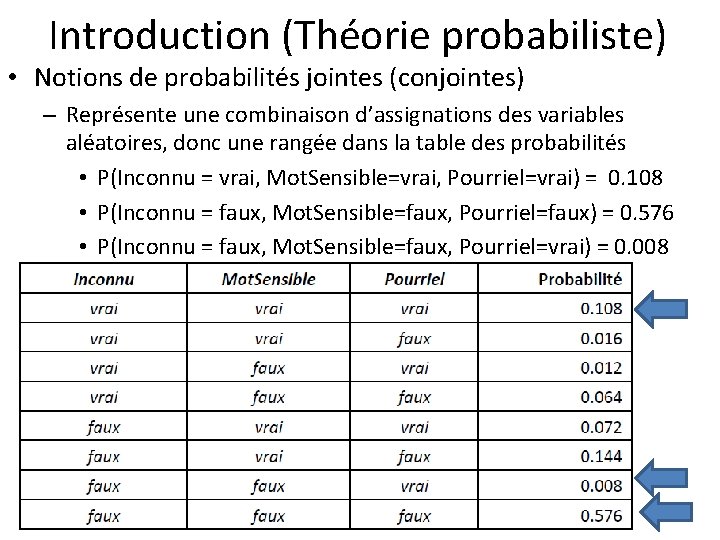
Introduction (Théorie probabiliste) • Notions de probabilités jointes (conjointes) – Représente une combinaison d’assignations des variables aléatoires, donc une rangée dans la table des probabilités • P(Inconnu = vrai, Mot. Sensible=vrai, Pourriel=vrai) = 0. 108 • P(Inconnu = faux, Mot. Sensible=faux, Pourriel=faux) = 0. 576 • P(Inconnu = faux, Mot. Sensible=faux, Pourriel=vrai) = 0. 008

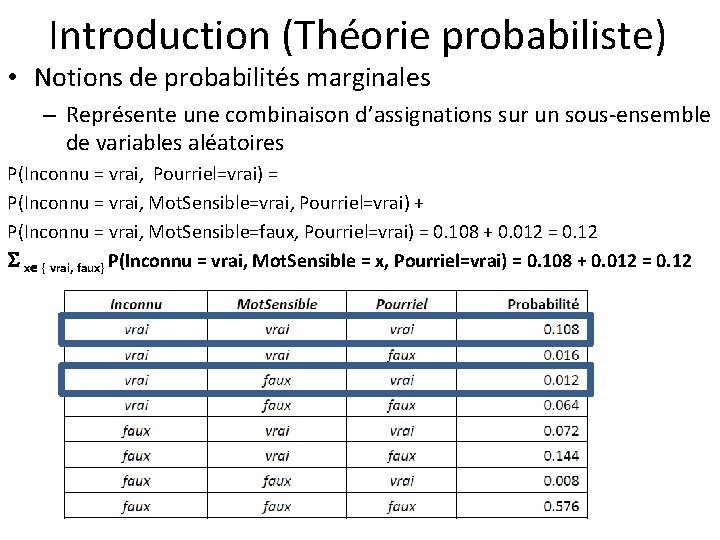
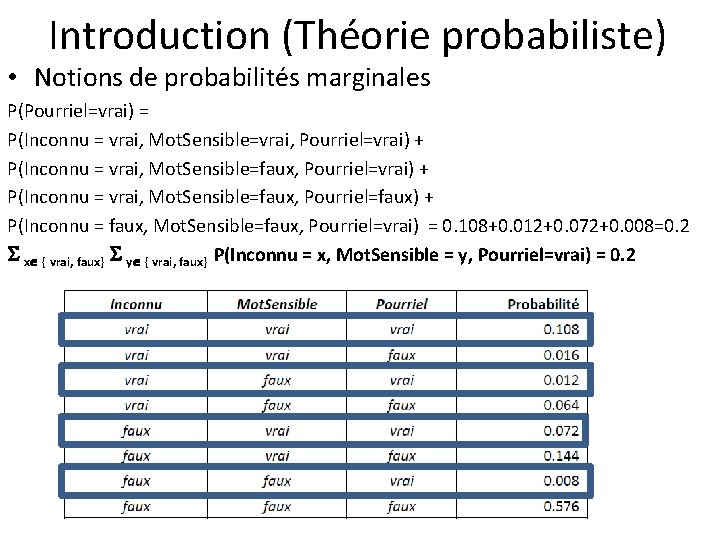
Introduction (Théorie probabiliste) • Notions de probabilités marginales – Représente une combinaison d’assignations sur un sous-ensemble de variables aléatoires P(Inconnu = vrai, Pourriel=vrai) = P(Inconnu = vrai, Mot. Sensible=vrai, Pourriel=vrai) + P(Inconnu = vrai, Mot. Sensible=faux, Pourriel=vrai) = 0. 108 + 0. 012 = 0. 12 x { vrai, faux} P(Inconnu = vrai, Mot. Sensible = x, Pourriel=vrai) = 0. 108 + 0. 012 = 0. 12

Introduction (Théorie probabiliste) • Notions de probabilités marginales P(Pourriel=vrai) = P(Inconnu = vrai, Mot. Sensible=vrai, Pourriel=vrai) + P(Inconnu = vrai, Mot. Sensible=faux, Pourriel=faux) + P(Inconnu = faux, Mot. Sensible=faux, Pourriel=vrai) = 0. 108+0. 012+0. 072+0. 008=0. 2 x { vrai, faux} y { vrai, faux} P(Inconnu = x, Mot. Sensible = y, Pourriel=vrai) = 0. 2

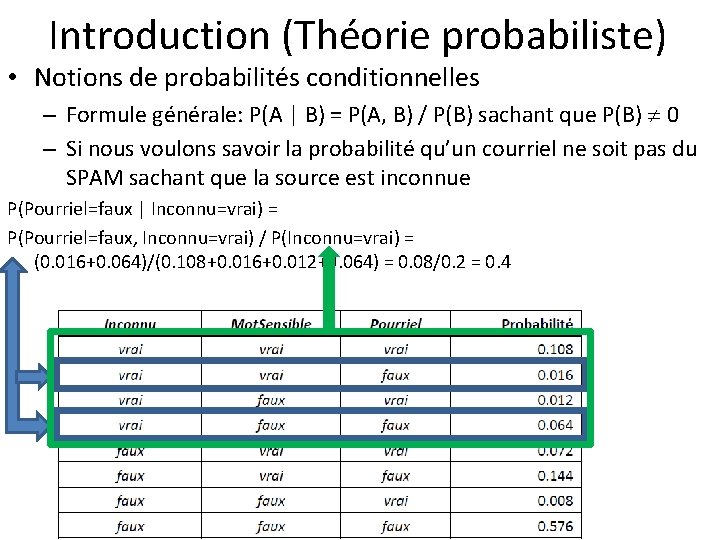
Introduction (Théorie probabiliste) • Notions de probabilités conditionnelles – Formule générale: P(A | B) = P(A, B) / P(B) sachant que P(B) 0 – Si nous voulons savoir la probabilité qu’un courriel ne soit pas du SPAM sachant que la source est inconnue P(Pourriel=faux | Inconnu=vrai) = P(Pourriel=faux, Inconnu=vrai) / P(Inconnu=vrai) = (0. 016+0. 064)/(0. 108+0. 016+0. 012+0. 064) = 0. 08/0. 2 = 0. 4

Introduction (Théorie probabiliste) • Règle du chaînage pour n variables aléatoires X 1, X 2, …. Xn = P(X 1) P(X 2 | X 1) P(X 3 | X 1, X 2) … P(Xn| X 1, . . Xn-1)

Introduction (Théorie probabiliste) • Avec la règle du chaînage il n’est plus nécessaire de spécifier toutes les probabilités jointes P(X 1, . . Xn), on pourrait plutôt spécifier P(X 1), P(X 2|X 1), P(X 3|X 1, X 2), . . . , P(Xn| X 1, . . . , Xn-1) • Nous pourrions alors spécifier les probabilités: • Et pouvoir ensuite calculer les probabilités P(Pourriel, Inconnu):

Introduction (Théorie probabiliste) • La règle de Bayes stipule que la probabilité: P(Cause|Effet) = P(Effet|Cause) P(Cause) / P(Effet) • Par exemple: P(Pourriel| Inconnu)=P(Inconnu|Pourriel) P(Pourriel)/ P(Inconnu) • P(Pourriel) est une probabilité à priori et représente notre croyance p/r au fait qu’un nouveau courriel soit un pourriel et ce avant toute observation. • P(Pourriel| Inconnu) est une probabilité à posteriori et représente notre croyance actualisée après avoir observé que l’auteur du courriel est inconnu (vrai). • Permet de déduire une probabilité diagnostique à partir d’une probabilité causale.

Introduction (Théorie probabiliste) • La règle de Bayes permet de déduire la probabilité: P(Pourriel=faux | Inconnu=vrai)

Introduction (Théorie probabiliste) • Des variables aléatoires A et B sont dites indépendantes SSI: • Si nous voulons calculer la probabilité jointe P(Pluie, Pourriel) = P(Pluie) P(Pourriel)

Introduction (Théorie probabiliste) • L’indépendance entre les variables permet de réduire la taille de la distribution de probabilités et de rendre les inférences plus efficaces, dans l’exemple précédent, nous n’avons qu’à stocker en mémoire P(Pluie=vrai) = 0. 3 et P(Pourriel=vrai) = 0. 1, plutôt que toute la table.

Introduction (Théorie probabiliste) • Notions d’indépendance conditionnelle – Si nous avons une carie, la probabilité que la sonde accroche dans la dent cariée ne dépend pas du fait que j’aie mal à cette dent ou non: • P(Accroche|Mal. Dents, Carie=vrai) = P(Accroche |Carie=vrai) – De même si je n’ai pas de carie: • P(Accroche|Mal. Dents, Carie=faux) = P(Accroche|Carie=faux) – On dit que Accroche est conditionnellement indépendante de Mal. Dents étant donnée Carie, puisque: • P(Accroche|Mal. Dents, Carie) = P(Accroche|Carie)

Introduction (Théorie probabiliste) • Notions d’indépendance conditionnelle – Réécrivons la probabilité jointe en utilisant la règle du chaînage 2 + 1 paramètres – Dans certains cas l’indépendance conditionnelle réduit la complexité de représentation de la distribution jointe de exponentielle (O(2 n)) à linéaire (O(n)).

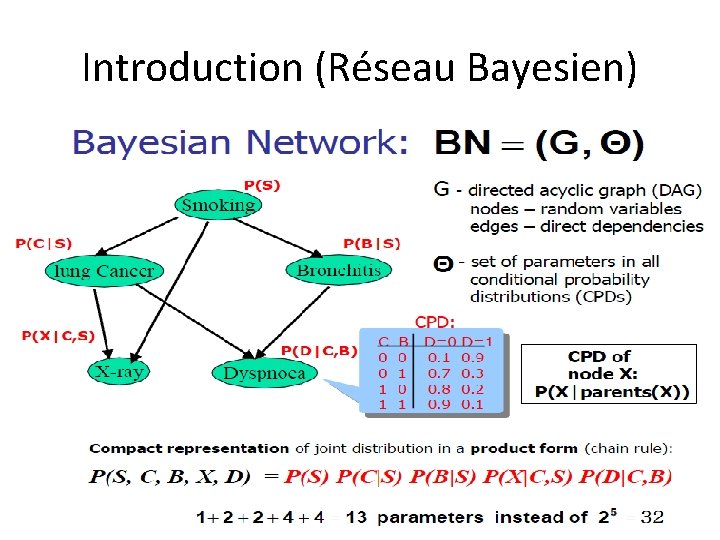
Introduction (Réseau Bayesien) • Représentation structurée, graphique de relations probabilistes entre variables aléatoires • Représentation explicite des dépendences et indépendances conditionnelles • Dépendances représentées par des arcs dans un graphe • Représentation efficiente des probabilités jointes • Permet de répondre à diverses requêtes • P (lung cancer=yes | smoking=no, positive X-ray=yes )=?

Introduction (Réseau Bayesien)

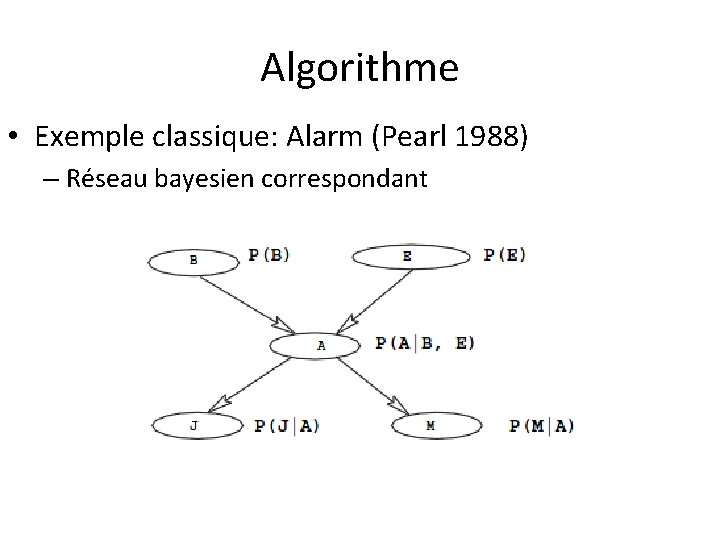
Introduction (Réseau Bayesien) • Un domaine d’application peut être modélisé par une suite de variables aléatoires X 1, X 2, X 3, …. , Xn • La connaissance contenue dans ce domaine d’application est représentée par la probabilité jointe P(X 1, X 2, X 3, …. , Xn) • Exemple classique: Alarm (Pearl 1988) – À LA, les vols et tremblements de terre sont communs, et déclenchent une alarme, dans ces cas Mary et John, les voisins téléphonent pour vérifier si quelqu’un est à la maison

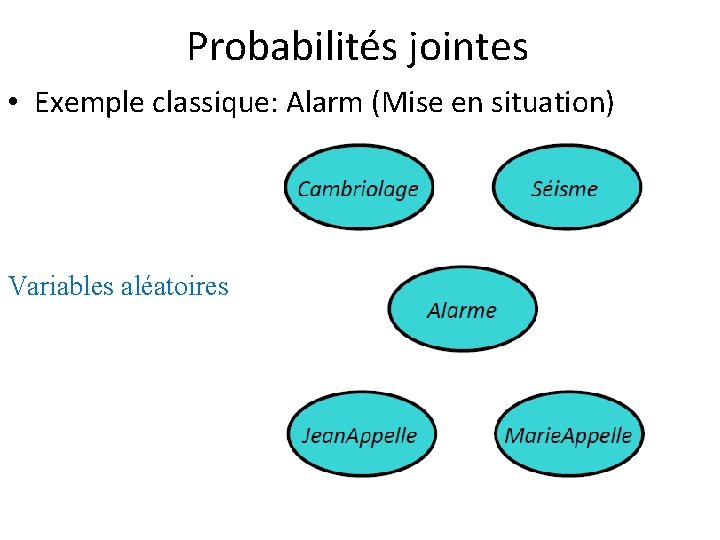
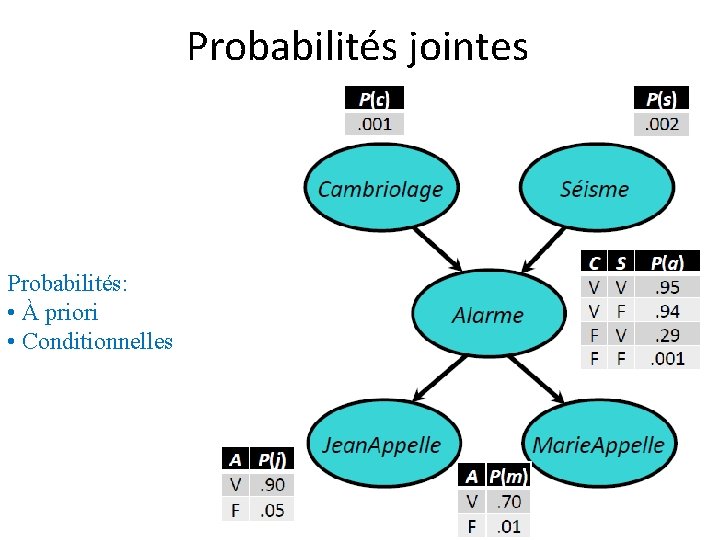
Probabilités jointes • Exemple classique: Alarm (Pearl 1988) – Variables: B (vols), E (tremblement de terre), A (alarme), J (John appel), M (Mary appel) – La probabilité jointe P(B, E, A, J, M) permet de modéliser l’information sous forme probabiliste

Probabilités jointes • Exemple classique: Alarm (Mise en situation)

Probabilités jointes • Exemple classique: Alarm (Mise en situation) Variables aléatoires

Probabilités jointes • Exemple classique: Alarm (Mise en situation) Liens de dépendances: • Expriment les liens de Causalité • Expriment les dépendances conditionnelles

Probabilités jointes Probabilités: • À priori • Conditionnelles

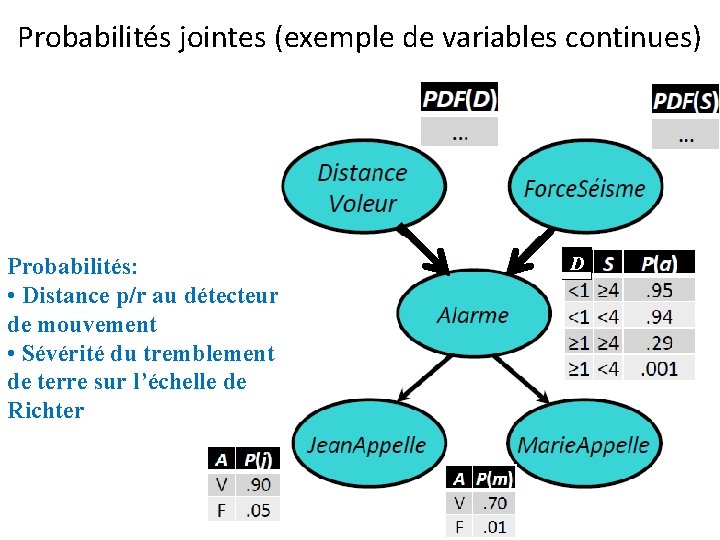
Probabilités jointes (exemple de variables continues) Probabilités: • Distance p/r au détecteur de mouvement • Sévérité du tremblement de terre sur l’échelle de Richter D

Probabilités jointes • Exemple classique: Alarm (Pearl 1988) – P(B, E, A, J, M)

Marginale/probabilité conditionnelle • Exemple classique: Alarm (Pearl 1988) – Quelle est la probabilité d’avoir un vol sachant que Mary appel, P(B=y|M=y) ? – Pour répondre à cette question, nous devons introduire des notions de marginalisation et de probabilité conditionnelle

Marginale/probabilité conditionnelle • Exemple classique: Alarm (Pearl 1988) – Pour répondre à cette question, nous devons introduire des notions de marginalisation et de probabilité conditionnelle

Marginale/probabilité conditionnelle • Exemple classique: Alarm (Pearl 1988) – Quelle est la probabilité d’avoir un vol sachant que Mary appel, P(B=y|M=y) ? 0. 000115/(0. 000115 + 0. 00015) = 0. 434

Marginale/probabilité conditionnelle • Exemple classique: Alarm (Pearl 1988) – Sachant que la probabilité jointe permet d’extraire les diverses relations entre les variables (informations), il devient alors possible de faire de l’inférence: • Inférence diagnostic: inférer les causes à partir d’effets (ex: médecine, déduire une maladie à partir de symptômes), P(B=y|M=Y) • Inférence prédictive: inférer les effets à partir des causes, P(M=y|B=y)

Marginale/probabilité conditionnelle • Exemple classique: Alarm (Pearl 1988) – Cependant, la probabilité jointe P(X 1, X 2, X 3, …. , Xn) requiert: • 2 n données pour spécifier les probabilités • Donc, difficile d’acquérir ces probabilités • Stockage exponentiel – Mais en exploitant l’indépendance conditionnelle et la règle de probabilité en chaîne (chain rule) il devient possible de réduire le nombres de paramètres requis pour évaluer les probabilités jointes

Règle de chaînage • Exemple classique: Alarm (Pearl 1988) – Chain rule (règle de chaînage)

Règle de chaînage • Exemple classique: Alarm (Pearl 1988) – Sachant que: – Alors: – Cette dernière opération comporte moins de termes

Règle du chaînage • Exemple classique: Alarm (Pearl 1988) – – CPT (conditional probability tables)

Algorithme • Exemple classique: Alarm (Pearl 1988) – Réseau bayesien correspondant

Algorithme • Algorithme de construction d’un réseau bayesien – Choisir un ensemble de n variables descriptives. – Choisir un ordre pour les variables. – À partir d’un réseau vide ajouter des variables 1 par 1 selon l’ordonnancement. – Pour ajouter la i ème variable X i • Déterminer pa(X ) dans (X 1 , . . . , X i-1) • Tel que P(X i |X 1, . . . , X i-1) = P(X i |pa(X i)) • Relier un arc entre les variables pa(X i) à X i. i 1

Algorithme • Ordre 1 (B, E, A, M, J)

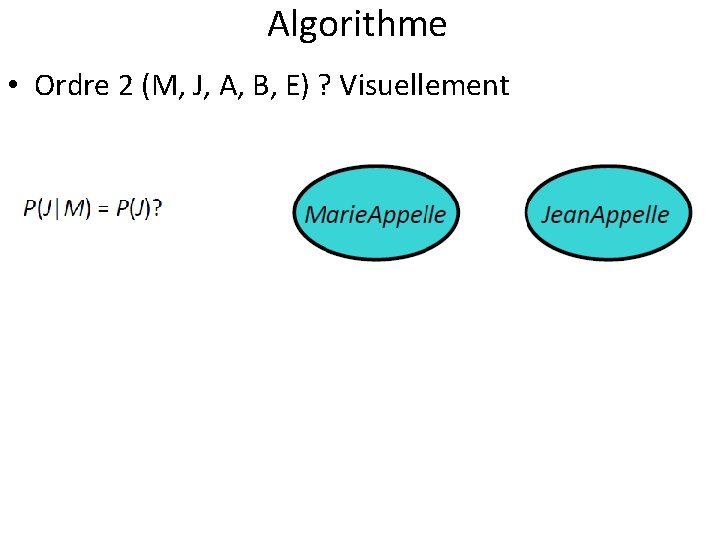
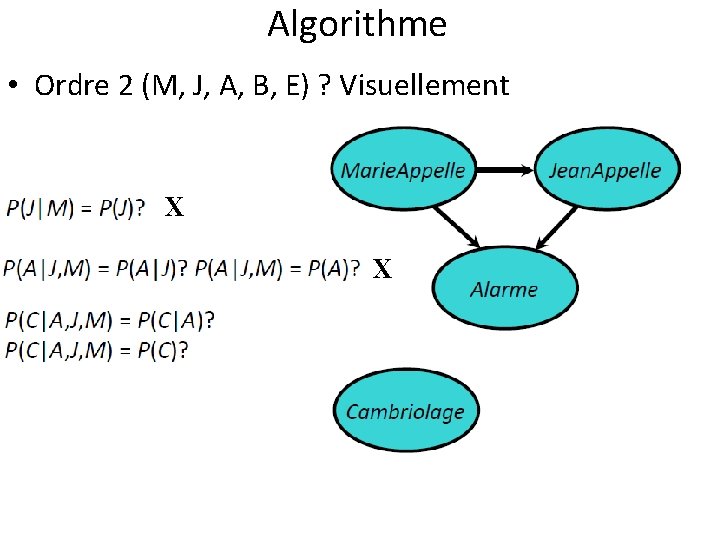
Algorithme • Ordre 2 (M, J, A, B, E) ?

Algorithme • Ordre 2 (M, J, A, B, E) ? Visuellement

Algorithme • Ordre 2 (M, J, A, B, E) ? Visuellement X

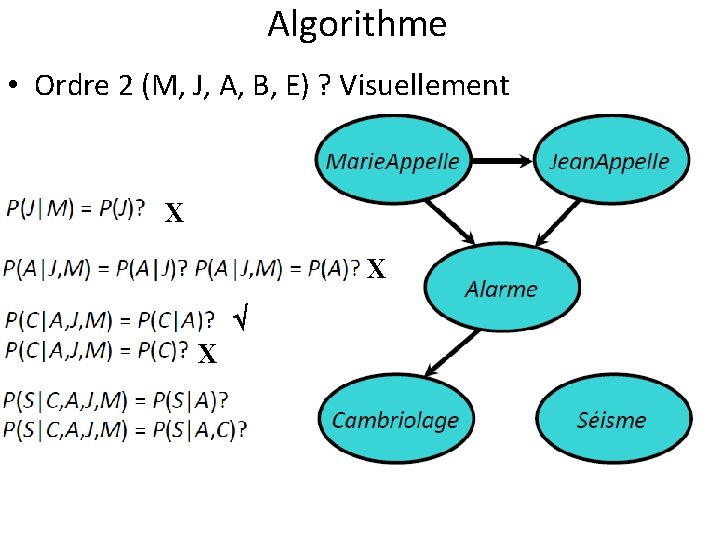
Algorithme • Ordre 2 (M, J, A, B, E) ? Visuellement X X

Algorithme • Ordre 2 (M, J, A, B, E) ? Visuellement X X X

Algorithme • Ordre 2 (M, J, A, B, E) ? Visuellement X X

Algorithme • Ordre 3 (M, J, E, B, A) ?

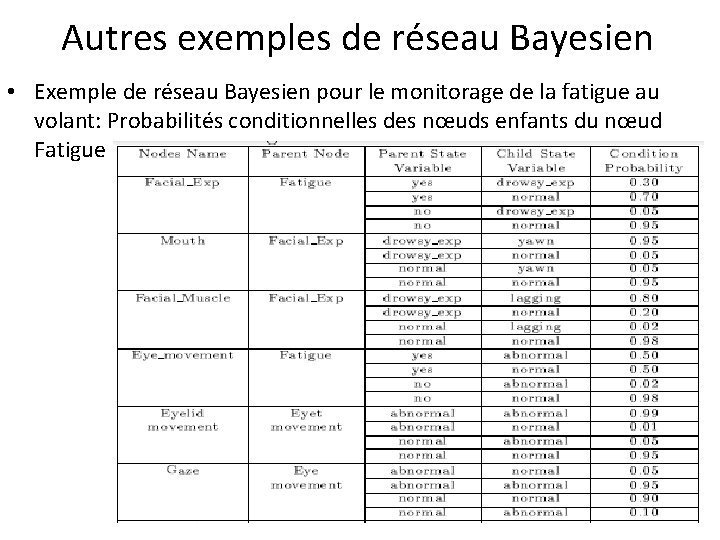
Autres exemples de réseau Bayesien • Exemple de réseau Bayesien pour le monitorage de la fatigue au volant (Information Fusion with Bayesian Metwork for Monitoring Human Fatigue, Ji et al. )

Autres exemples de réseau Bayesien • Exemple de réseau Bayesien pour le monitorage de la fatigue au volant: Probabilités à priori

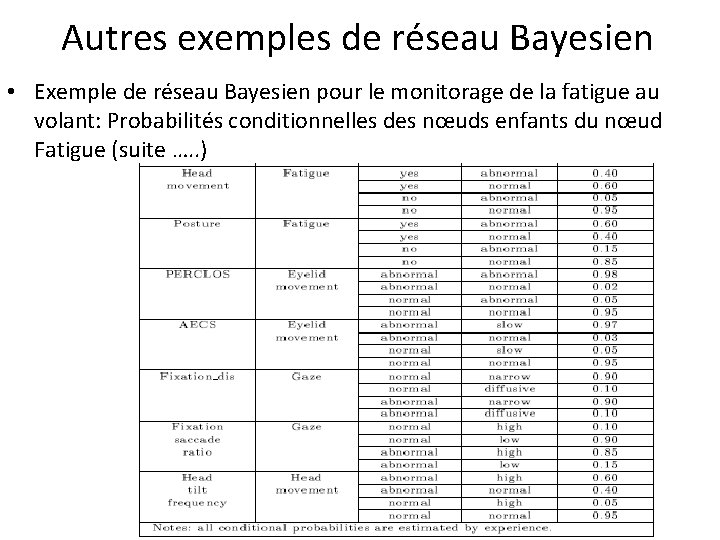
Autres exemples de réseau Bayesien • Exemple de réseau Bayesien pour le monitorage de la fatigue au volant: Probabilités conditionnelles des nœuds enfants du nœud Fatigue

Autres exemples de réseau Bayesien • Exemple de réseau Bayesien pour le monitorage de la fatigue au volant: Probabilités conditionnelles des nœuds enfants du nœud Fatigue (suite …. . )

Autres exemples de réseau Bayesien • Exemple de réseau Bayesien pour le monitorage de la fatigue au volant: Résultats d’inférence du réseau Bayesien MSBNx permet de faire ces inférences • Top-Down (conditions Environnementales) • Buttom-Up (informations Visuelles)

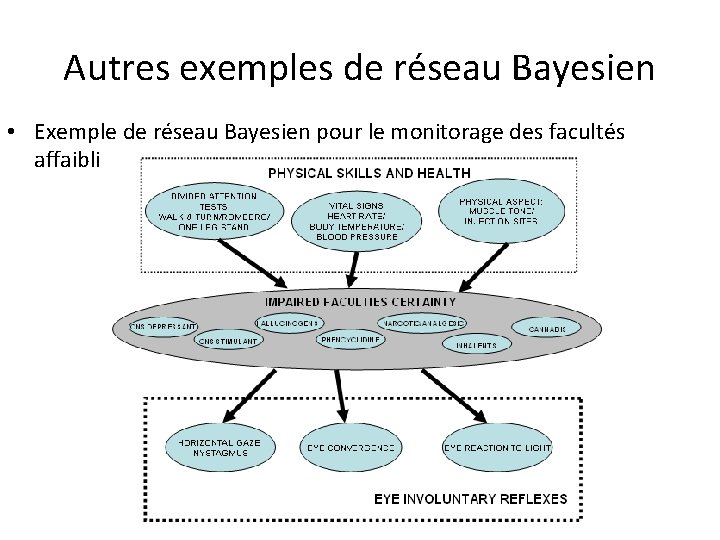
Autres exemples de réseau Bayesien • Exemple de réseau Bayesien pour le monitorage des facultés affaiblies

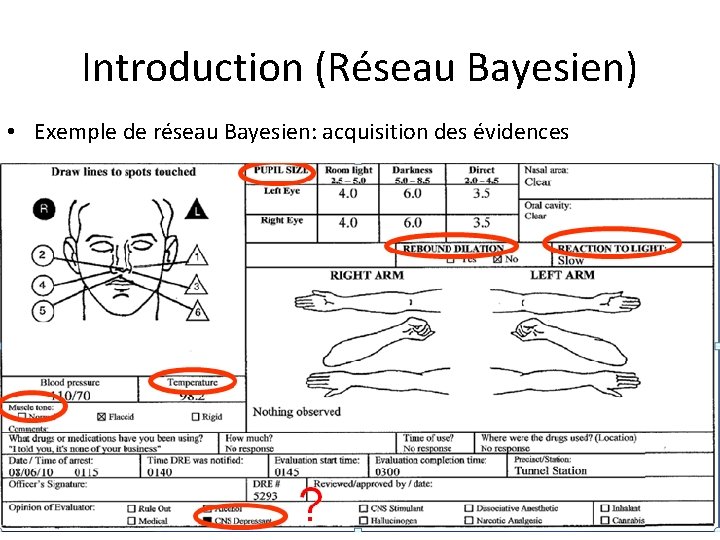
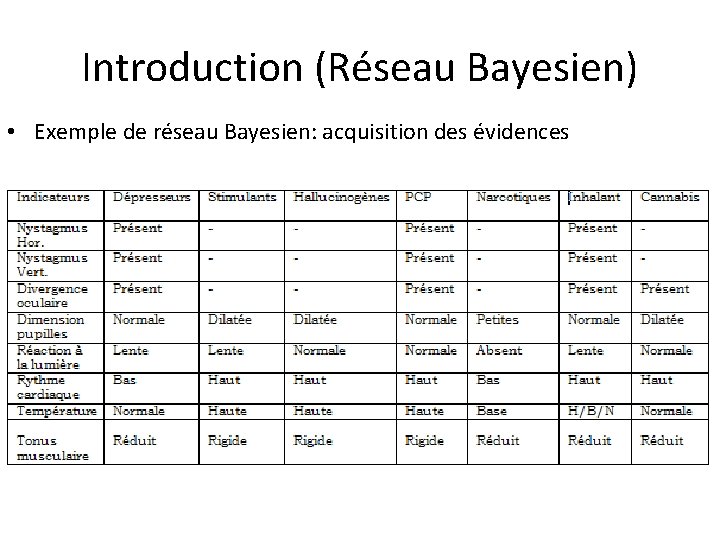
Autres exemples de réseau Bayesien • Exemple de réseau Bayesien: acquisition des évidences

Autres exemples de réseau Bayesien • Exemple de réseau Bayesien: acquisition des évidences

Introduction (Réseau Bayesien) • Exemple de réseau Bayesien: acquisition des évidences

Introduction (Réseau Bayesien) • Exemple de réseau Bayesien: acquisition des évidences