Integration using substitution 4 3 Substitution This allows

Integration using substitution 4. 3

Substitution • This allows us to integrate a composite function. • Two ideas: • Pattern recognition (substitution that can be done mentally) • Change of variables (with written substitution steps)

Antidifferentiation of a Composite Function • Let g be a function whose range is in an interval, and let f be a function that is continuous on the same interval. If g is differentiable on its domain and F is the antiderivative of f, then:

Pattern Recognition • Each of the following Integrands fit the pattern f(g(x))g’(x). Identify the pattern and evaluate the Integral. • A) • B) • C)

Using the same patterns… • These next three integrals are very similar. Show you can multiply or divide by a constant to evaluate.

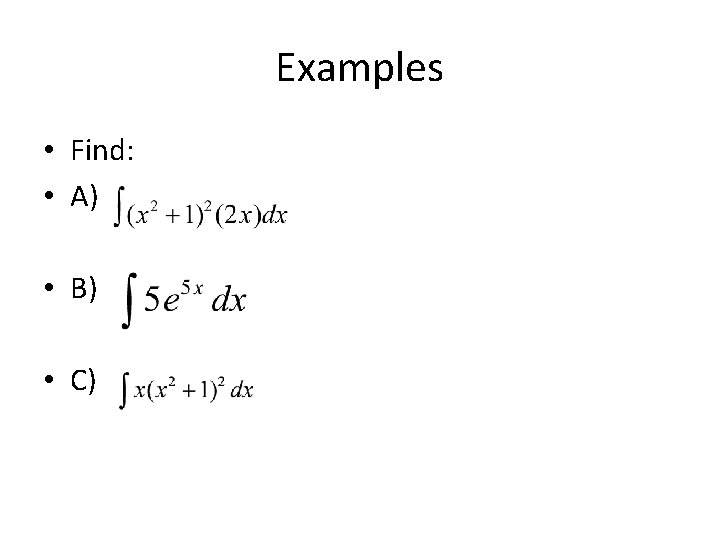
Examples • Find: • A) • B) • C)

Change of Variables • For a change of variables you completely rewrite the integral in terms of u and du.

Guidelines for u substition • 1) Choose a substitution u=g(x). Usually it is best to choose the inside part of your composite function. • 2) Compute du = g’(x)dx. This is the derivative of u. • 3) Rewrite the integral in terms of u and du and find the integral. • 4) Replace any remaining u value with the equivalent g(x). • 5) Check by differentiating.

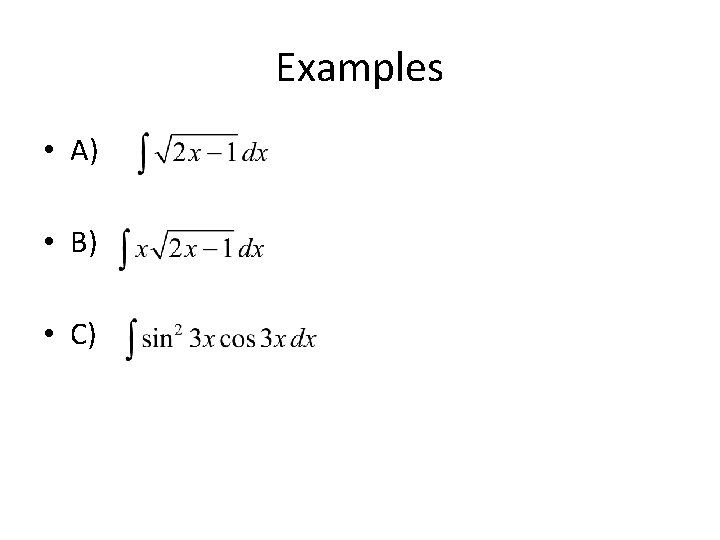
Examples • A) • B) • C)

General Power Rule for Integration • If g is a differentiable function of x, then • Or if u = g(x)

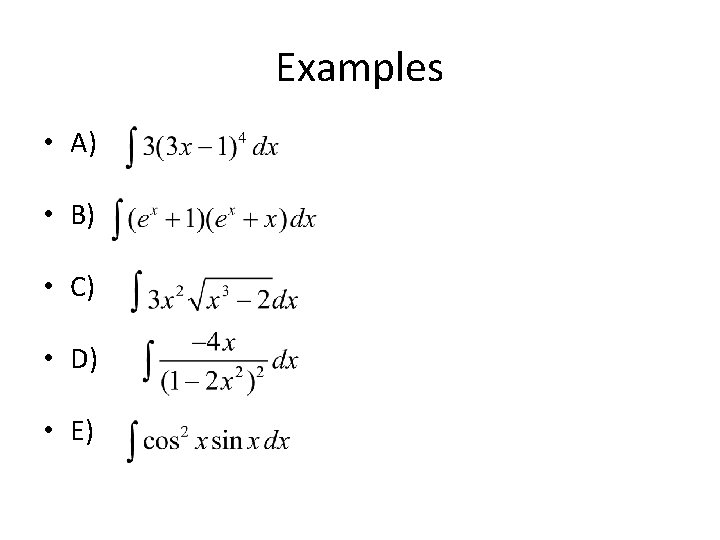
Some integrals don’t work with general power rule

Change of Variables for Definite Integrals • The limits of integration (ie a and b) must be rewritten in terms of u. -If the function u = g(x) has a continuous derivative on a closed interval [a, b] and f is continuous on the range of g, then

What does this look like? • U Substitution Geometric View • http: //tube. geogebra. org/student/m 90751 • https: //tube. geogebra. org/student/m 90752

Evaluate using change of variables

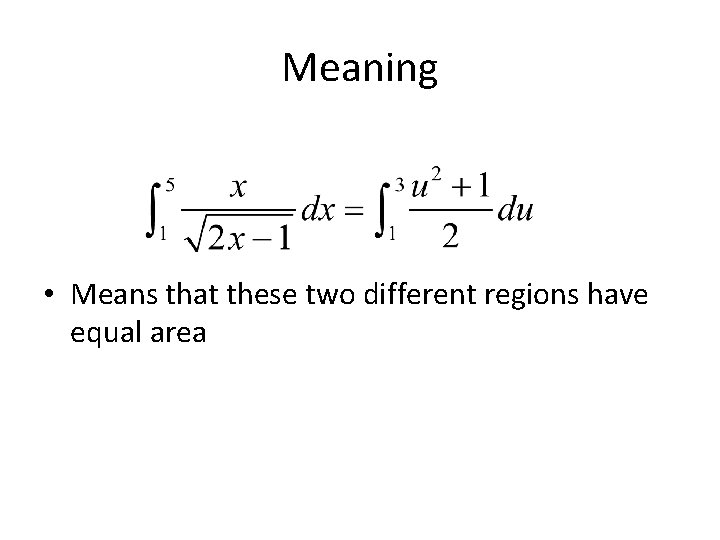
Meaning • Means that these two different regions have equal area

Even and Odd Function trick • Let f be integrable on the closed interval [-a, a] • 1) If f is an even function, then • 2) If f is an odd function, then

HW • Pg. 340 • 7, 9, 11, 13, 17, 19, 23, 49, 53, 55, 57, 65, 67, 87, 91 • Pg. 340 • 95 to 111 odd, 137, 139, 142, 143