Integration of Trigonometric Functions Integration Since integration is

Integration Since integration is the reverse of differentiation, for the trig ratios we have

Integration Since indefinite integration is the reverse of differentiation, we get So, The rule

Integration However, we can’t integrate all compound functions in this way. Let’s try the

Integration What is the important difference between and ? So, the important difference is

Examples Integration Find 1. Solutions: 1. 2.

Integration We found earlier that so, You need to remember this exception to the

Integration e. g. Find We have a function of a function. . . but

Integration e. g. Find Which double angle formula can we use to change the

Integration The previous example is an important application of a double angle formula. The

Examples 1. Find Solution: So, Integration

Slides: 20

Download presentation

Integration of Trigonometric Functions

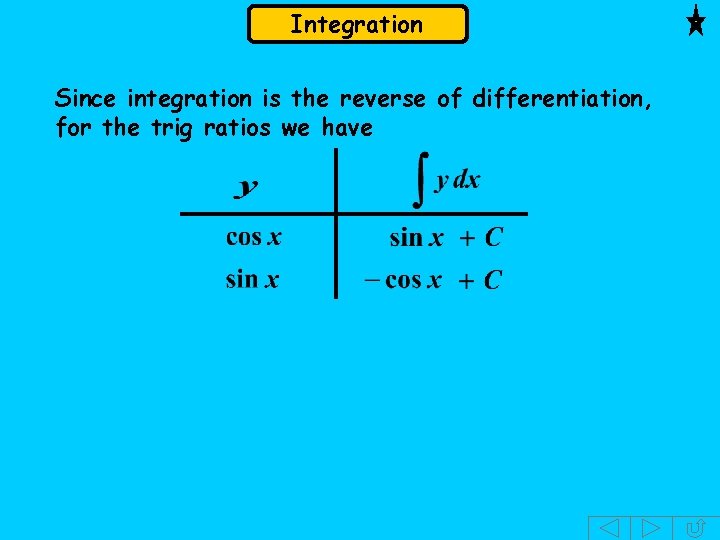
Integration Since integration is the reverse of differentiation, for the trig ratios we have

Integration Since indefinite integration is the reverse of differentiation, we get So, The rule is: 3 3 If we divide C by 3, we get Ø integrate the outer another functionconstant, say C 1, but we usually just write C.

Integration Since indefinite integration is the reverse of differentiation, we get So, The rule is: Ø integrate the outer function Ø divide by the derivative of the inner function

Integration Since indefinite integration is the reverse of differentiation, we get So, the rule is: Ø integrate the outer function Ø divide by the derivative of the inner function Tip: We can check the answer by differentiating it. We should get the function we wanted to integrate.

Integration

Integration However, we can’t integrate all compound functions in this way. Let’s try the rule on another example: e. g. THIS IS WRONG ! Ø integrate the outer function Ø divide by the derivative of the inner function

Integration However, we can’t integrate all compound functions in this way. Let’s try the rule on another example: e. g. THIS IS WRONG ! The rule has given us a quotient, which, if we differentiate it, gives:

Integration What is the important difference between and ? So, the important difference is that the 1 st example has an inner function that is linear; it differentiates to a constant. The 2 nd is non-linear. We can’t integrate it.

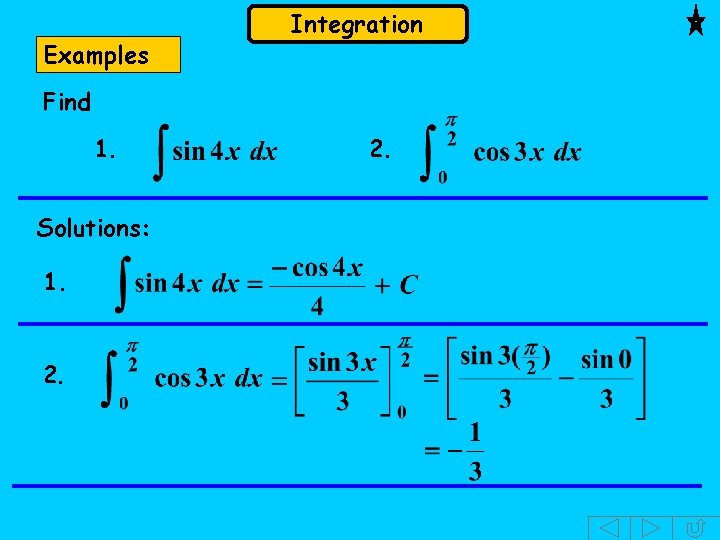
Examples Integration Find 1. Solutions: 1. 2.

Integration We found earlier that so, You need to remember this exception to the general rule that we can only integrate directly if the inner function is linear. We also have, for example,

Integration e. g. Find We have a function of a function. . . but the inner function. . .

Integration e. g. Find We have a function of a function. . . but the inner function. . . is not linear. However, we can use a trig formula to convert the function into one that we can integrate.

Integration e. g. Find Which double angle formula can we use to change the function so that it can be integrated? ANS: Rearranging the formula: So,

Integration The previous example is an important application of a double angle formula. The next 2 are also important. Examples 1. Find 2. Find

Examples 1. Find Solution: So, Integration

Integration 2. Find Solution: So,