INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS Rational

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS Rational function: Example Find

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS

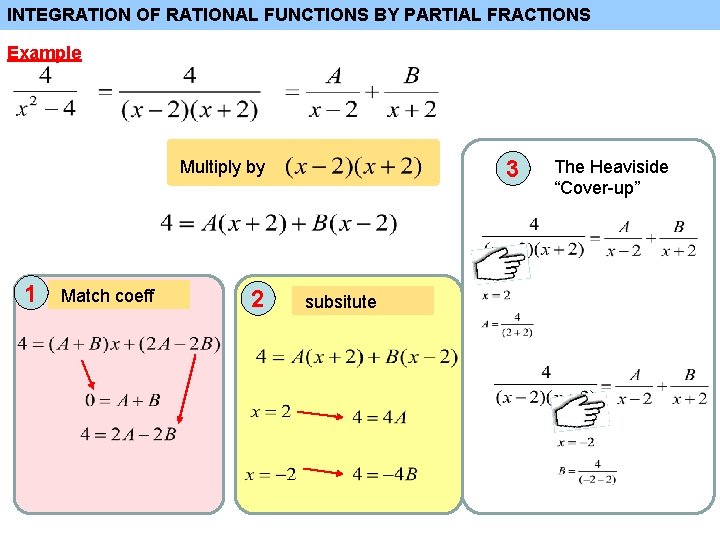
INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS Example Multiply by 1 Match coeff 2 subsitute 3 The Heaviside “Cover-up”

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS irreducible quadratic factor linear factor reducible quadratic factor all factors are irreducible

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS 1 2 3 Use long division Check if we can use subsitution Factor q(x) as linear factors or irreducible quadratic 4 q(x)= product of linear factor All distinct case 1 Some repeated case 2 Express p(x)/q(x) as a sum of partial fraction q(x)= product of quadratic (irred) All distinct case 3 repeated case 4

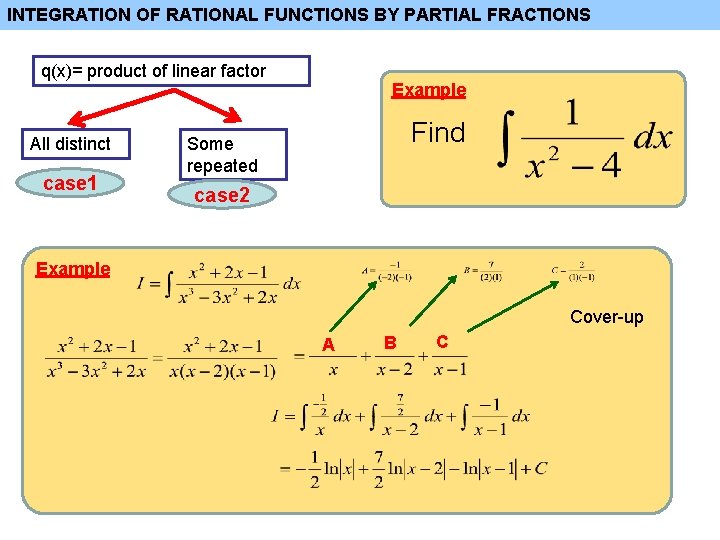
INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS q(x)= product of linear factor All distinct case 1 Example Find Some repeated case 2 Example Cover-up A B C

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS F 132

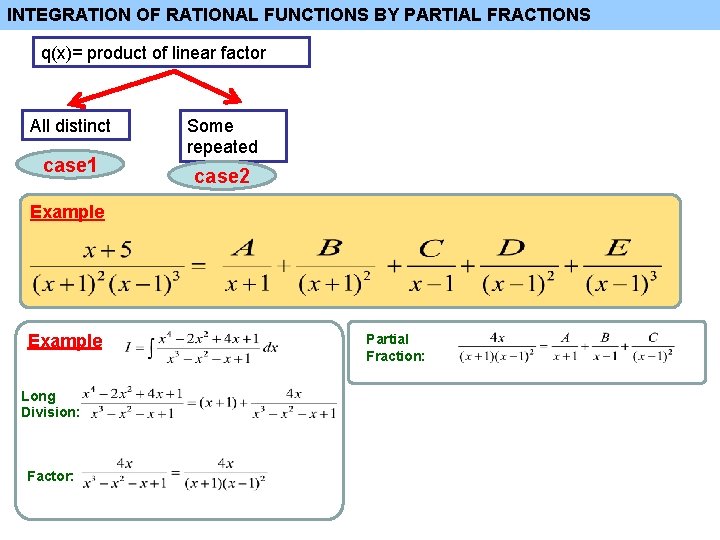
INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS q(x)= product of linear factor All distinct case 1 Some repeated case 2 Example Long Division: Factor: Partial Fraction:

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS q(x)= product of linear factor All distinct case 1 Example Some repeated case 2

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS F 132

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS q(x)= product of quadratic (irred) All distinct case 3 Example repeated case 4 Expand by partial fraction (DONOT EVALUATE )

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS 081

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS 952

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS q(x)= product of linear factor All distinct case 1 Some repeated Example Long Division: case 2 Factor: Remark: only use subsitue method or match coeff to find the constants A, B, C, D, E. Partial Fraction: Multiply: subsitute: Integrate:

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS Multiply by (denominator) Find the constants Sum of the coeff F 141

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS F 142 Expand by partial Find the constants Evaluate the integral substitution tan^-1 Evaluate the integral

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS RATIONALIZING SUBSTITUTIONS Some nonrational functions can be changed into rational functions Example Find

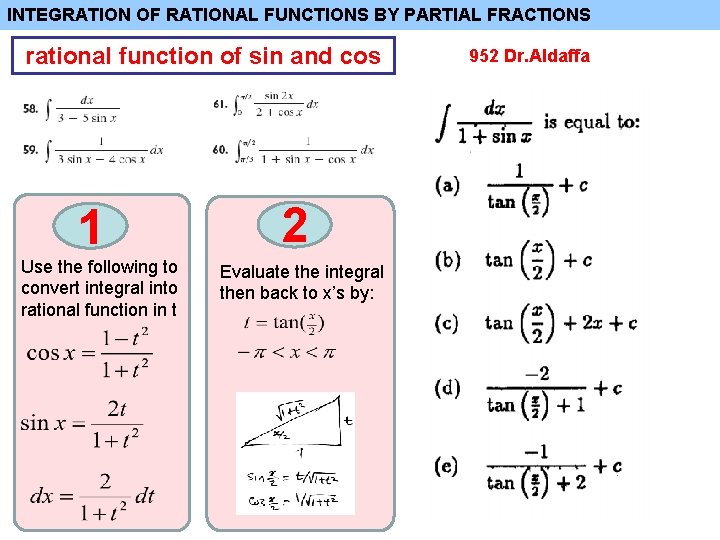
INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS rational function of sin and cos 1 Use the following to convert integral into rational function in t 2 Evaluate the integral then back to x’s by: 952 Dr. Aldaffa

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS rational function of sin and cos 1 Use the following to convert integral into rational function in t 2 Evaluate the integral then back to x’s by:

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS Remark: make sure that 1) 2) 3) Deg( numerator ) < Deg( denominator ) Each factor is irreducible No cancelations ( num & denom ) How to figure that a quadratic factor is irreducible Discriminant is negative

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS q(x)= product of linear factor All distinct case 1 Some repeated Example Long Division: case 2 Factor: Remark: only use subsitue method or match coeff to find the constants A, B, C, D, E. Partial Fraction: Multiply: subsitute: Integrate:

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS Expand by partial Find the constants Evaluate the integral subsitution tan^(-1)

INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS