Integration in physics Why Do We Need Integration

Integration in physics

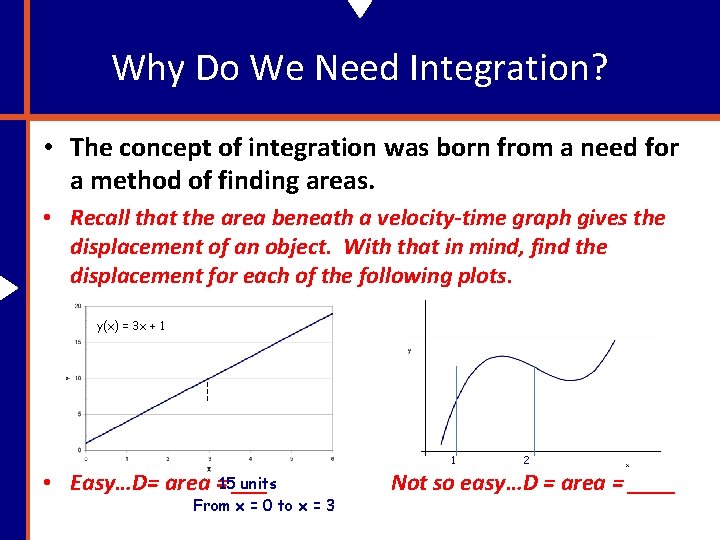
Why Do We Need Integration? • The concept of integration was born from a need for a method of finding areas. • Recall that the area beneath a velocity-time graph gives the displacement of an object. With that in mind, find the displacement for each of the following plots. y(x) = 3 x + 1 units • Easy…D= area =15___ From x = 0 to x = 3 1 2 Not so easy…D = area = ____

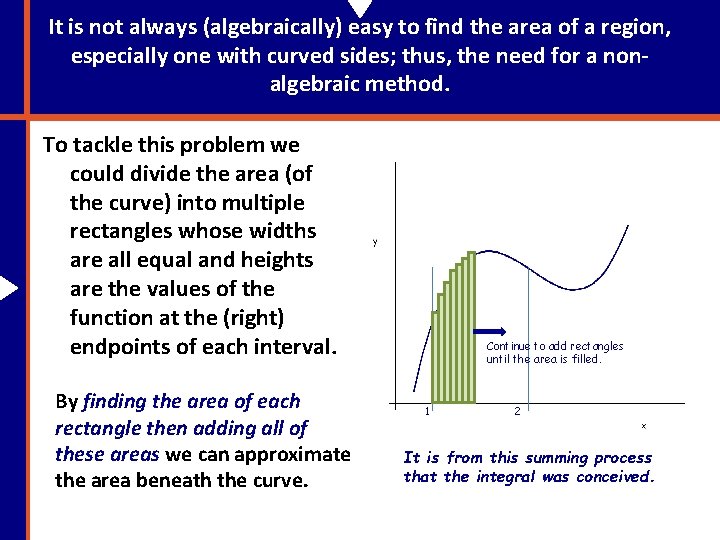
It is not always (algebraically) easy to find the area of a region, especially one with curved sides; thus, the need for a nonalgebraic method. To tackle this problem we could divide the area (of the curve) into multiple rectangles whose widths are all equal and heights are the values of the function at the (right) endpoints of each interval. By finding the area of each rectangle then adding all of these areas we can approximate the area beneath the curve. Continue to add rectangles until the area is filled. 1 2 It is from this summing process that the integral was conceived.

So…what is integration? • Although (as you will learn in your calculus classes) the process of integration is not always simple; the fundamental idea behind the process of integration is a simple idea. • You can simply think of a “integration” as just a fancy name that describes the process of finding the antiderivative of a function. • Obviously there is more, mathematically, to discuss…

Let’s Start Simply…. 1) Derivatives: What is the derivative of 3 x 2+ 2 x + 5? (2)3 x + (1)2 = 6 x + 2 2) Integrals: What do you take the derivative of to get 2 x? x 2 + C Congratulations…you have just found the antiderivative. The derivative and integral are reverse processes

Notation Integrand The function to integrate Limits of Integration Variable of Integration What you integrate w/r/t Integration Symbol An elongated “S” from the Latin “summa” meaning sum.

Indefinite Integrals • Indefinite integral will not have limits of integration. The result of integrating is a function. Example… G(x) = (2 x 2 + 12 x + 6)dx = ? ? ? Answer… = 2/3 x 3 + 6 x 2 + 6 x + C Whoa…what is this and why is it here?

Definite Integrals • Definite integral will have limits of integration • The result is a number. • This is governed by the Fundamental Theorem of Calculus If f is continuous on [a, b], then where F is the antiderivative of f.

An example… Find the antiderivative and evaluate. The constant always cancels when finding a definite integral, so we leave it out!

Some Simple Rules of Integration …other shortcuts. • The subject of integration is a huge branch of mathematics in of itself and cannot possibly be contained here in this one tutorial. Hopefully, though, you now have some knowledge and appreciation for what atitderivatives are. The following are commonly known formulas for antiderivatives.

In physics…. Position x(t) Velocity v(t) Acceleration a(t) Differentiate Integrate You will, of course, see other applications in physics… … but this is where we start.