Integration by parts Product Rule Integration by parts

Integration by parts Product Rule:

Integration by parts Let dv be the most complicated part of the original integrand that fits a basic integration Rule (including dx). Then u will be the remaining OR Let u be a portion of the integrand whose derivative is a function simpler than u. Then dv will be the remaining factors (including dx).

Integration by parts u=x dv= exdx du = dx v = ex

Integration by parts u = lnx du = 1/x dx dv= x 2 dx v = x 3 /3

Integration by parts u = arcsin x dv= dx v=x

Integration by parts u = x 2 dv = sin x dx du = 2 x dx v = -cos x u = 2 x dv = cos x dx du = 2 dx v = sin x

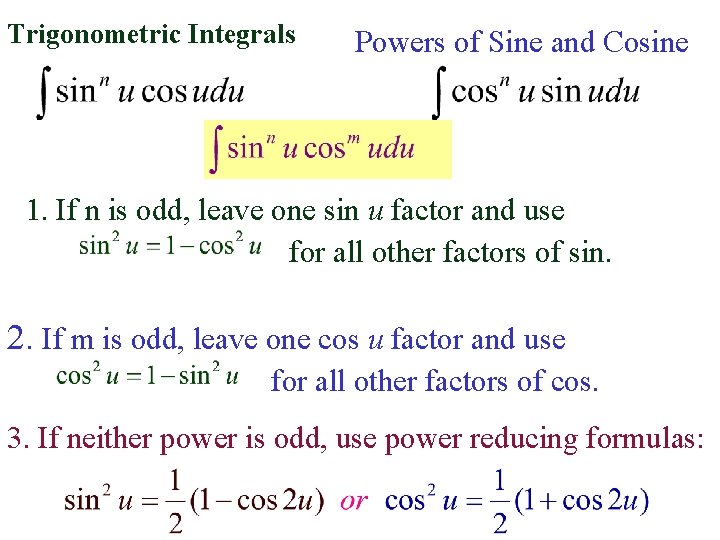
Trigonometric Integrals Powers of Sine and Cosine 1. If n is odd, leave one sin u factor and use for all other factors of sin. 2. If m is odd, leave one cos u factor and use for all other factors of cos. 3. If neither power is odd, use power reducing formulas:

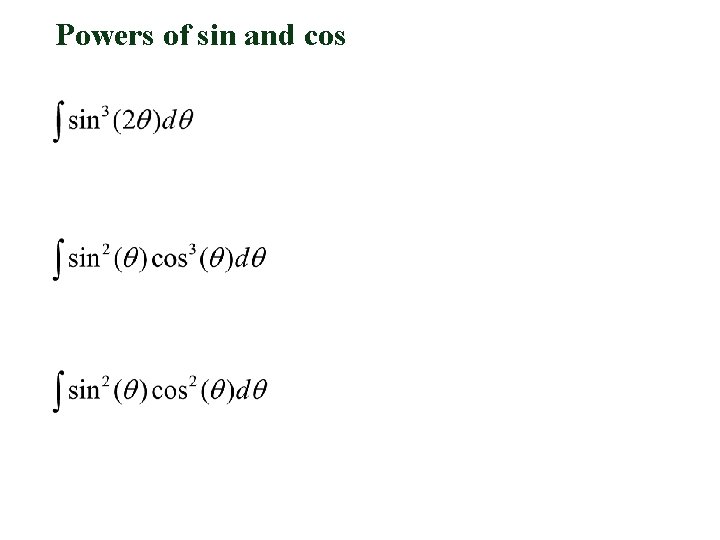
Powers of sin and cos

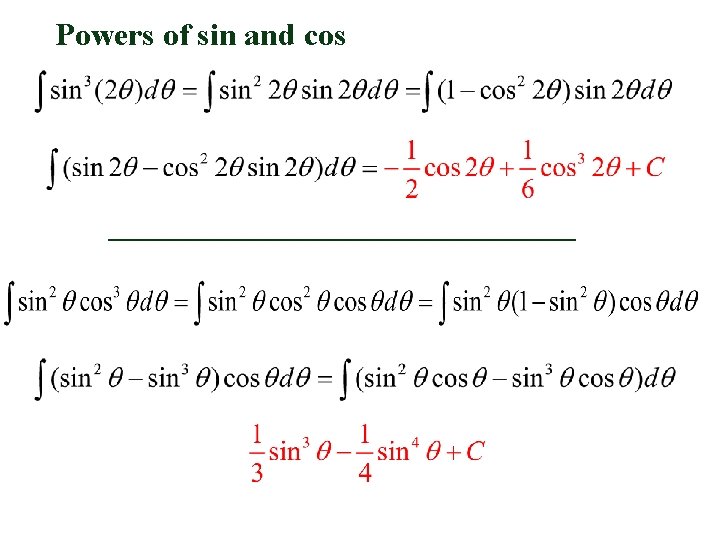
Powers of sin and cos

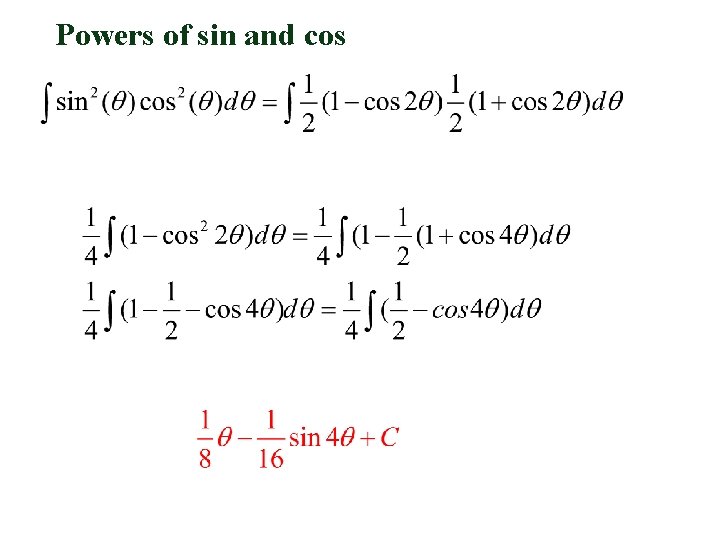
Powers of sin and cos

Tangents and secants Create an integral that is shown above.

Eliminating radicals by trig substitution. Pythagorean identities: Let u = a sin θ

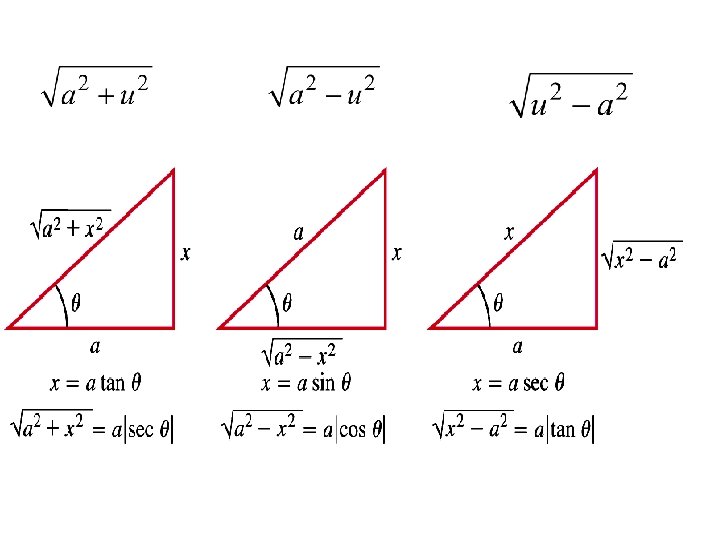
Trig Substitutions

Ex: Let x = a sin θ = 3 sin θ dx = 3 cos θ dθ

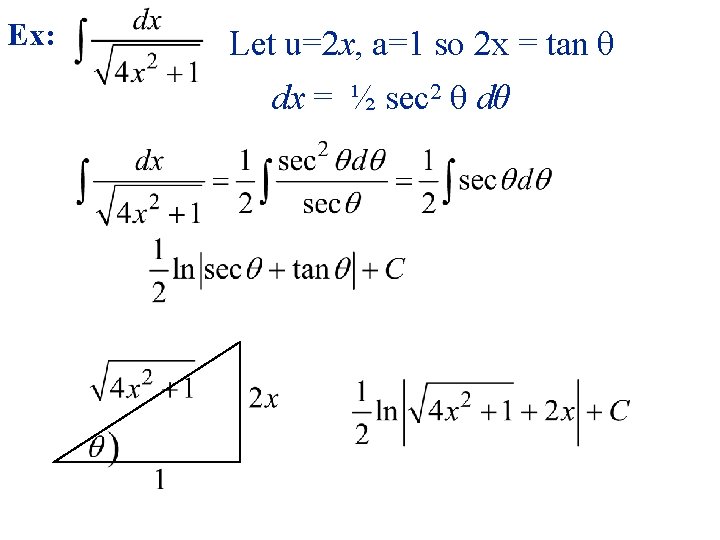
Ex: Let u=2 x, a=1 so 2 x = tan θ dx = ½ sec 2 θ dθ

Partial Fractions If x = 2: If x =3: 1=-B so B = -1 1=A

Partial Fractions-Repeated linear factors If x =0: 6= A If x = -1: -9 = -C, so C = 9 If x = 1: 31=6(4)+2 B+9, B = - 1

Quadratic Factors If x = 0 then A = 2 If x = 1 then B = -2 If x = -1 If x = 2 2 = -C +D 8 = 2 C+D Solving the system of equations you find C = 2 and D = 4.

Repeated quadratic Factors For third degree: A=8 For second degree: B=0 For first degree: 13=2 A+C For constant: D+2 B=0

Repeated quadratic Factors A=8 B=0 13=2 A+C D+2 B=0 So, D=0 and C = -3

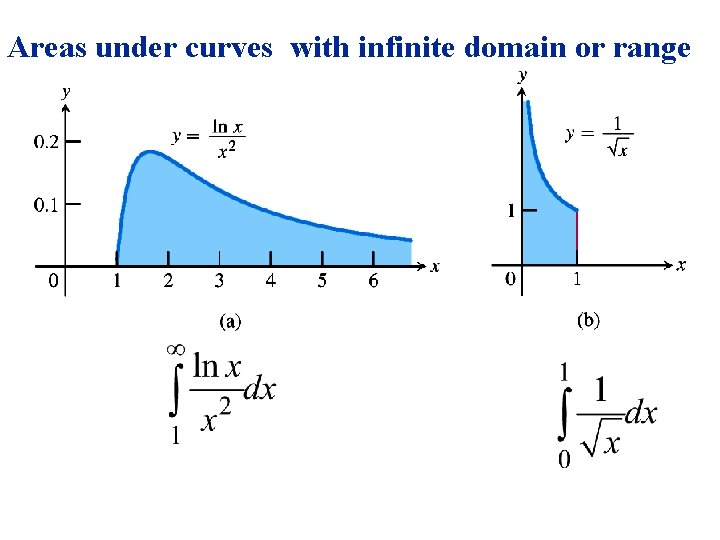
Areas under curves with infinite domain or range

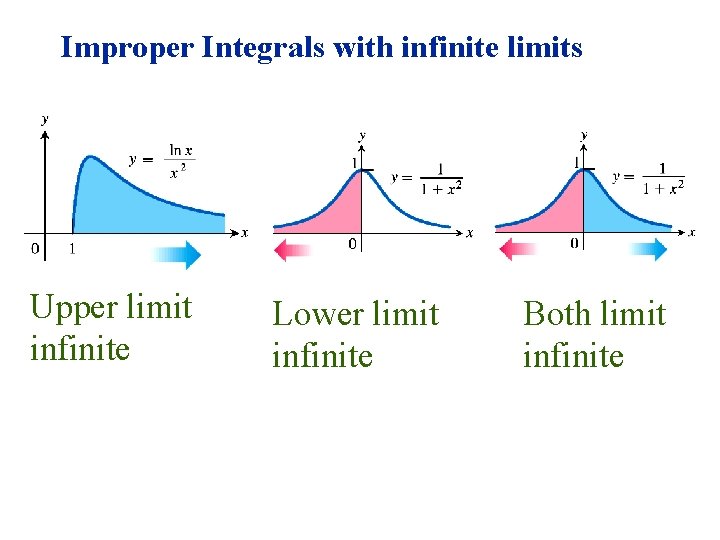
Improper Integrals with infinite limits Upper limit infinite Lower limit infinite Both limit infinite

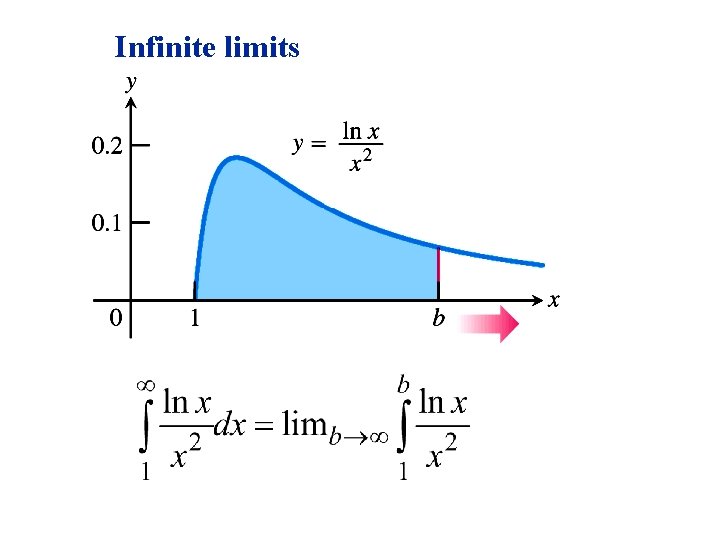
Infinite limits

Evaluation Use L’Hôpital’s rule We say the improper integral CONVERGES to The value of 1. (The area is finite. )

When both limits are infinite

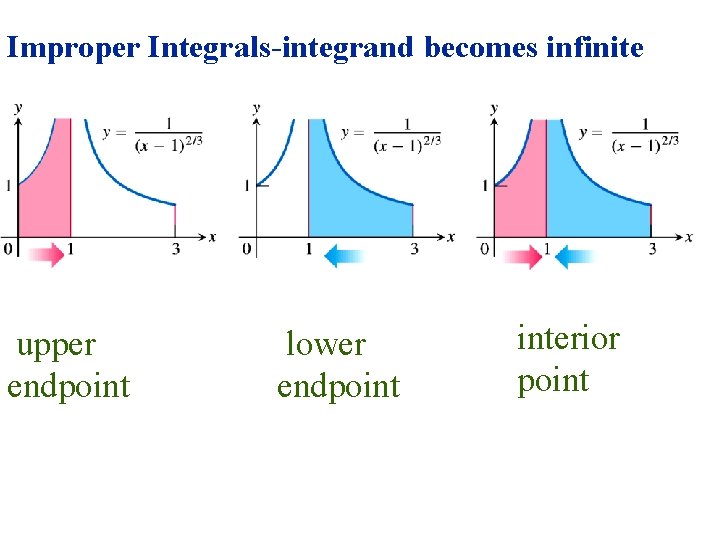
Improper Integrals-integrand becomes infinite upper endpoint lower endpoint interior point

Integrals with Infinite discontinuities. The integral converges to 2.

Calculation with infinite discontinuity

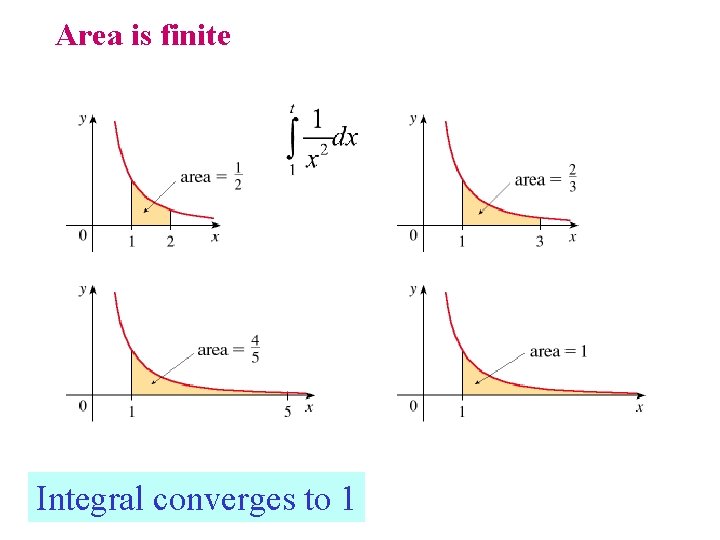
Area is finite Integral converges to 1

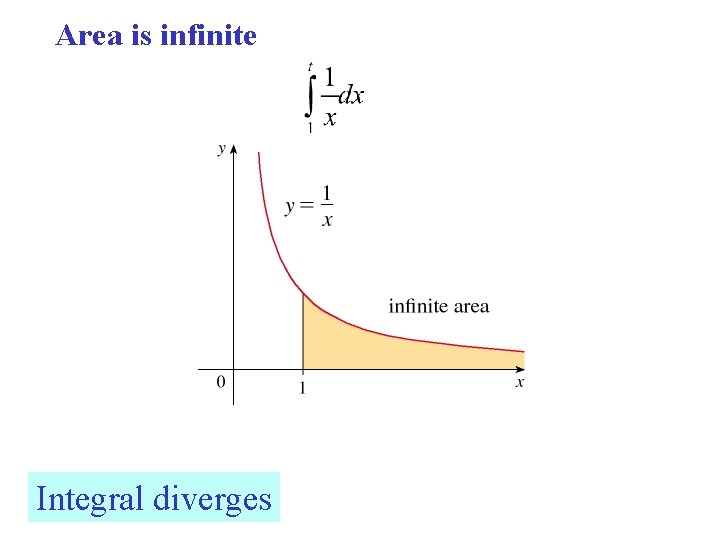
Area is infinite Integral diverges

Integrals of the form

Convergence or divergence Integrals of the form Converge if p > 1 and diverge if p = 1 or p < 1. Which of the following converge and which diverge?

Direct comparison test If f and g are continuous functions with f(x) g(x) For all x a. Then…. . Converges if Converges A function converges if its values are smaller than another function known to converge. Diverges if Diverges A function diverges if its values are larger than another function known to diverge.

Limit Comparison test for convergence If f and g are positive and continuous on [a, ) And if Then the integrals and both converge or both diverge: If If then diverges and also diverges.