Integration Algebra Using Proof in Algebra Section 2

Integration Algebra: Using Proof in Algebra Section 2. 4

Integration Algebra: Using Proof in Algebra This section we will review the properties of equality that are useful for algebra in general and for geometric proofs specifically. We will specifically talk about the reflexive, symmetric, and transitive property of equality. In this section we formalize their definition and use. 9/10/2020 …Geo. Sec 02_04. ppt 2

Integration Algebra: Using Proof in Algebra Set theory deals with things (called elements or members) that we put in the same container. Thus, the set of ALL cats does not have any dogs in that set. The set of ALL house pets would include both cats and dogs, but not ALL cats and dogs are house pets. It is important to understand what is and is not in a set. 9/10/2020 …Geo. Sec 02_04. ppt 3

Integration Algebra: Using Proof in Algebra Mathematicians are always looking for new number systems that have specific relation properties. One of the most desirable relation is called an equivalence relation. An equivalence relation is defined are a relation that is reflexive, symmetric, and transitive. The concept of the equality relation (i. e. , = symbol) is an equivalence relation and as we continue in this course we will find that congruence, , is an equivalence relation. 9/10/2020 …Geo. Sec 02_04. ppt 5

Integration Algebra: Using Proof in Algebra An element in set A has an equality relation with itself. Specifically, it is equal to itself. This property is called reflexive since it is a reflection of itself. This represents a relation. A a 3 In the case to the left, a 1 = a 1 For example; 5 = 5 or x=x a 2 9/10/2020 …Geo. Sec 02_04. ppt 6

Integration Algebra: Using Proof in Algebra If the order of the relation (in this case equality) does not matter, then the relation is called symmetric. You can think of this as looking the same on both sides of the equality symbol. A c In the case to the left, if a = b, then b = a a For example; if 5 = 2 + 3, then 2 + 3 = 5 b 9/10/2020 …Geo. Sec 02_04. ppt 7
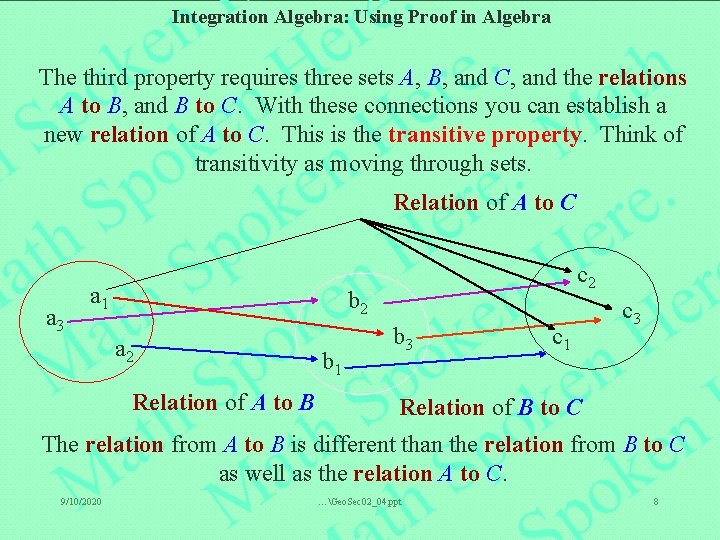
Integration Algebra: Using Proof in Algebra The third property requires three sets A, B, and C, and the relations A to B, and B to C. With these connections you can establish a new relation of A to C. This is the transitive property. Think of transitivity as moving through sets. Relation of A to C a 3 a 1 c 2 b 2 a 2 Relation of A to B b 1 b 3 c 1 c 3 Relation of B to C The relation from A to B is different than the relation from B to C as well as the relation A to C. 9/10/2020 …Geo. Sec 02_04. ppt 8

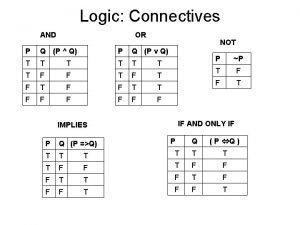
Integration Algebra: Using Proof in Algebra Properties of Equality for Real Numbers Reflexive Property For every number a, a = a. Symmetric Property For all numbers a and b, if a = b, then b = a. Transitive Property For all numbers a, b, and c, if a = b and b = c, then a = c Addition and Subtraction Properties For all numbers a, b, and c, if a = b, then a + c = b + c and a-c=b-c. Multiplication and Division Properties For all numbers a, b, and c, if a = b, then a • c = b • c and a/ = b/ , c 0. c c Substitution Property For all numbers a and b, if a = b, then a may be replaced by b in any equation or expression. Distributive Property For all numbers a, b, and c, a(b + c) = ab + ac 9/10/2020 …Geo. Sec 02_04. ppt 9
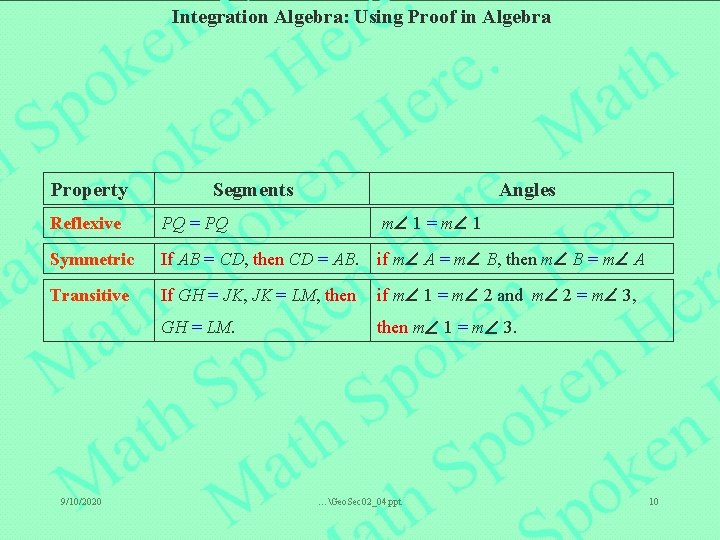
Integration Algebra: Using Proof in Algebra Property Segments Angles Reflexive PQ = PQ m 1 = m 1 Symmetric If AB = CD, then CD = AB. if m A = m B, then m B = m A Transitive If GH = JK, JK = LM, then if m 1 = m 2 and m 2 = m 3, GH = LM. then m 1 = m 3. 9/10/2020 …Geo. Sec 02_04. ppt 10

Integration Algebra: Using Proof in Algebra Summary In this section we established the reflexive, symmetric, and transitive properties of equality that you will use throughout the remainder of this course. We briefly established that segments and angles, from an equality perspective, are also reflexive, symmetric, and transitive. We will use these properties in the next section to show that congruence is reflexive, symmetric, and transitive. 9/10/2020 …Geo. Sec 02_04. ppt 11

Integration Algebra: Using Proof in Algebra END OF LINE 9/10/2020 …Geo. Sec 02_04. ppt 12
- Slides: 11