Integrating DiffieHellman Key Exchange into the Digital Signature

Integrating Diffie-Hellman Key Exchange into the Digital Signature Algorithm (DSA) Source: IEEE Communications Letters, Vol. 8, No. 3, March 2004 Authors: Lein Harn, Manish Mehta, Wen. Jung Hsin Speaker: Yu-Wei Su Date: 2004/09/29 1

Outline o o Introduction Concept & Goal Proposed Protocol Conclusion 2

1. Introduction o o 1 -1. 1 -2. 1 -3. 1 -4. Key Exchange Diffie-Hellman Algorithm Digital Signature DSA 3

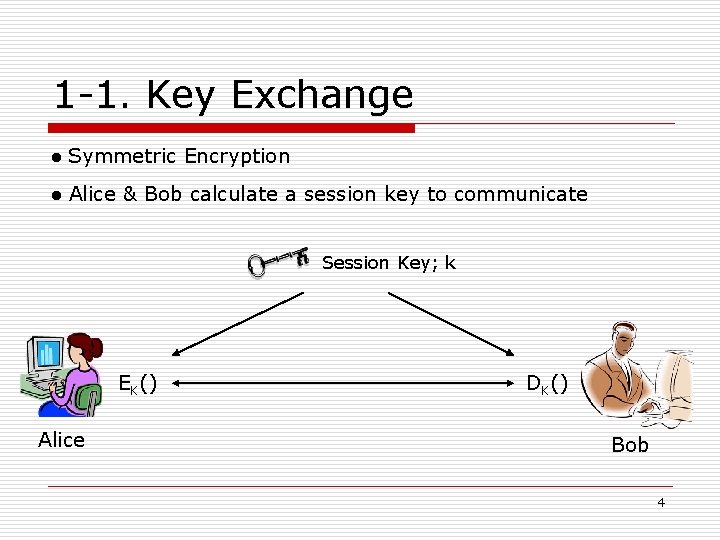
1 -1. Key Exchange ● Symmetric Encryption ● Alice & Bob calculate a session key to communicate Session Key; k EK() Alice DK() Bob 4

1 -2. Diffie-Hellman Algorithm Parameters (1/4) common parameters: g, p: two large primes, g < p private parameters: a: random number, choice by Alice b: random number, choice by Bob 5

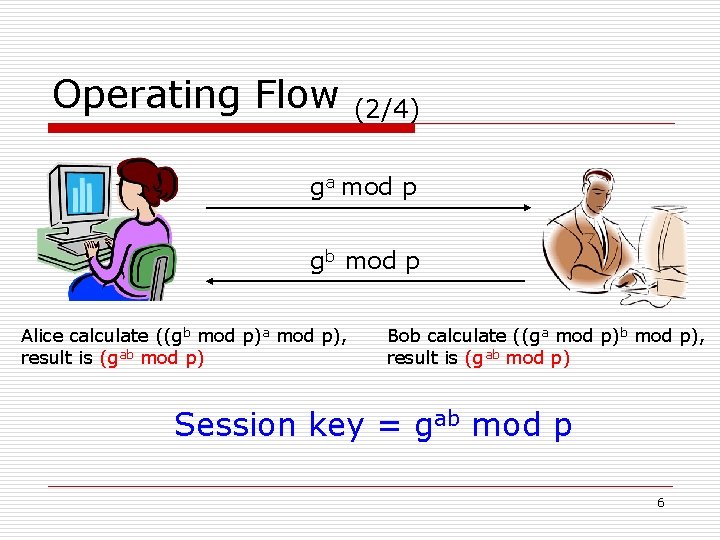
Operating Flow (2/4) ga mod p gb mod p Alice calculate ((gb mod p)a mod p), result is (gab mod p) Bob calculate ((ga mod p)b mod p), result is (gab mod p) Session key = gab mod p 6

Example p = 11, g = 2 a=4 b=8 (3/4) => ga mod p = 24 mod 11 = 5 gb mod p = 28 mod 11 = 3 Alice : (gb mod p)a mod p = 34 mod 11 = 4 Bob: (ga mod p)b mod p = 58 mod 11 = 4 Session key = 4 7

The Computational Diffie-Hellman Assumption(CDH assumption) (4/4) ● Eve receives (ga mod p) and (gb mod p) in the channel. ● It is very hard to calculate (gab mod p). 8

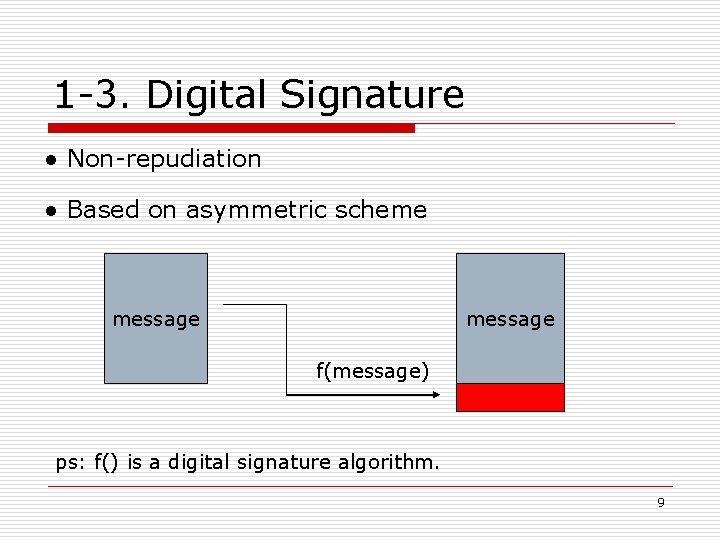
1 -3. Digital Signature ● Non-repudiation ● Based on asymmetric scheme message f(message) ps: f() is a digital signature algorithm. 9

1 -4. Digital Signature Algorithm(DSA) 1 -4 -1. Preview o Used in Digital Signature Standard(DSS) o Proposed by NIST o Published in FIPS PUB 186 -x o http: //www. itl. nist. gov/fipspubs 10

1 -4 -2. Parameters (1/3) Global parameters: p: a prime number, |p| = 512 ~ 1024 (bits), multiple of 64 q: a 160 -bit prime factor of (p-1) h: 1< h < p-1 g = (h(p-1)/q) mod p H(): a hash function, ex: SHA-1 Sender’s Private Parameter: x, random integer with 0 < x < q 11

Parameters (2/3) Sender’s Public Parameter: y = gx mod p m: message Per-Message Secret Parameter: k: random integer with 0 < k < q 12

Signing & Verifying (3/3) Signing (Sender) : r = (gk mod p) mod q s = [k-1(H(m) + xr)] mod q; ps: [(k-1)k] mod q = 1 => signature = (r, s) Verifying (Receiver) : w = (s)-1 mod q u 1 = [H(m)w] mod q u 2 = (r)w mod q v = [(gu 1 yu 2) mod p] mod q Test v ? = r 13

2. Concept & Goal 2 -1. DH + DSA Diffie-Hellman Algorithm + Digital Signature Algorithm = Take (gr mod p) as message in DSA 14

2 -2. Three Models In DSS, User’s have authenticated public key & private key 1. One-round protocol 2. Two-round protocol 3. Three-round protocol 15

3. Proposed protocol 3 -1. Parameters (based on DSS) User A, B: two users in protocol YA, XA: a key pair, public key & private key of user A in DSA, authenticated. YA = g. XA mod p YB, XB: a key pair, public key & private key of user B in DSA, authenticated. YB = g. XB mod p Other parameters are corresponding in DSA KAB: session key from A to B 16

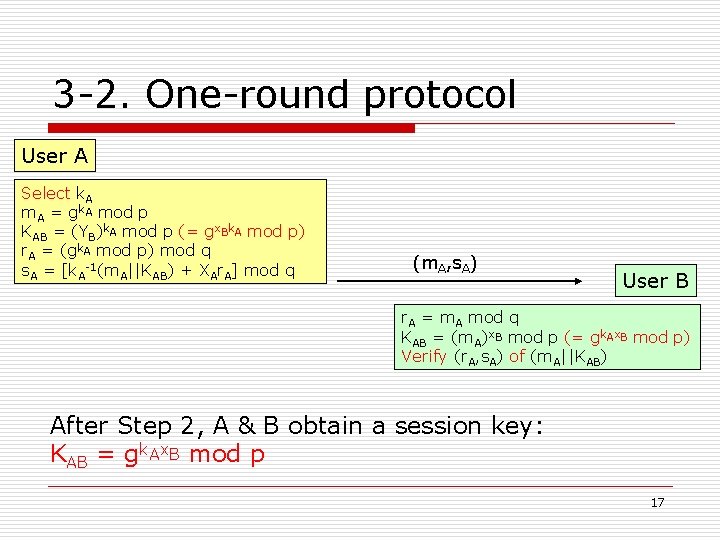
3 -2. One-round protocol User A Select k. A m. A = gk. A mod p KAB = (YB)k. A mod p (= gx. Bk. A mod p) r. A = (gk. A mod p) mod q s. A = [k. A-1(m. A||KAB) + XAr. A] mod q (m. A, s. A) User B r. A = m. A mod q KAB = (m. A)x. B mod p (= gk. Ax. B mod p) Verify (r. A, s. A) of (m. A||KAB) After Step 2, A & B obtain a session key: KAB = gk. Ax. B mod p 17

3 -3. Two-round protocol Step 1, Step 2 are the same as one-round protocol. User B User A (m. B, s. B) r. B = m. B mod q KBA = (m. B)x. A mod p (= gk. Bx. A mod p) Verify (r. B, s. B) of (m. B||KBA) k. B m. B = gk. B mod p KBA = (YA)k. B mod p (= gx. Ak. B mod p) r. B = (gk. B mod p) mod q s. B = [k. B-1(m. B||KBA) + XBr. B] mod q Sent (m. B, s. B) to User A After Step 4, A & B obtain two session keys: KAB = gk. Ax. B mod p KBA = gk. Bx. A mod p 18

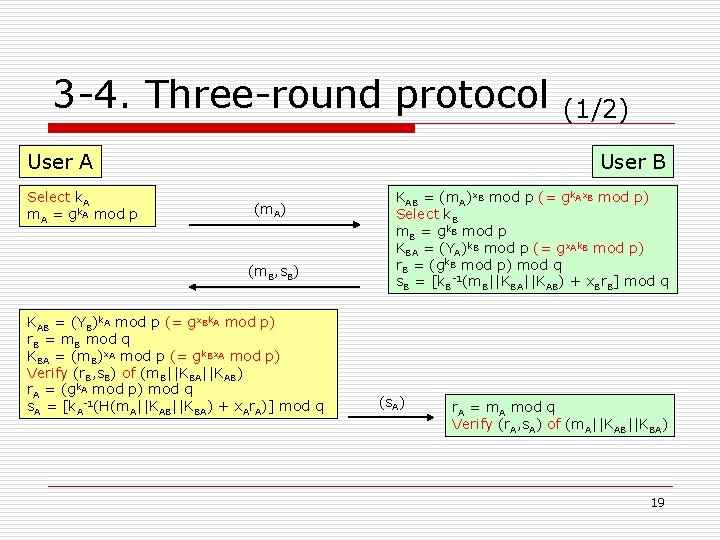
3 -4. Three-round protocol User A Select k. A m. A = gk. A mod p (1/2) User B (m. A) (m. B, s. B) KAB = (YB)k. A mod p (= gx. Bk. A mod p) r. B = m. B mod q KBA = (m. B)x. A mod p (= gk. Bx. A mod p) Verify (r. B, s. B) of (m. B||KBA||KAB) r. A = (gk. A mod p) mod q s. A = [k. A-1(H(m. A||KAB||KBA) + x. Ar. A)] mod q KAB = (m. A)x. B mod p (= gk. Ax. B mod p) Select k. B m. B = gk. B mod p KBA = (YA)k. B mod p (= gx. Ak. B mod p) r. B = (gk. B mod p) mod q s. B = [k. B-1(m. B||KBA||KAB) + x. Br. B] mod q (s. A) r. A = m. A mod q Verify (r. A, s. A) of (m. A||KAB||KBA) 19

4. Conclusion o Authentication & Efficient 20