Integrating A Key Distribution Procedure Into The Digital

Integrating A Key Distribution Procedure Into The Digital Signature Standard B. Arazi Electronics Letters Vol. 29, No. 11, Pg. 966 -967 May 1993 Weaknesses In Some Recent Key Agreement Protocols K. Nyberg, R. A. Rueppel Electronics Letters Vol. 30, No. 1, Pg. 26 -27 January 1994 Integrating Diffie-Hellman Key Exchange Into The Digital Signature Algorithm (DSA) Lein Harn, M. Mehta, W. -J. Hsin IEEE Communications Letters Vol. 8, No. 3, Pg. 198 -200 March 2004 Adviser: Min-Shiang Hwang Student: CSONGK (鍾松剛)

The Motivations (Arazi, 1993) n The DSS is only suitable to generate signatures on documents which are also transmitted in clear q n n The distribution of secret keys by DSS is ruled out The DH can not authenticate the actual involved parties Solution: Join them up!!

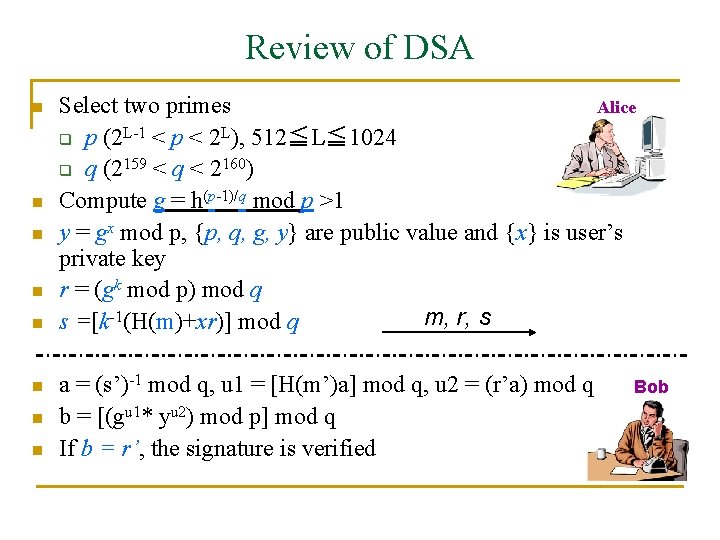
Review of DSA n n n n Alice Select two primes q p (2 L-1 < p < 2 L), 512≦L≦ 1024 q q (2159 < q < 2160) Compute g = h(p-1)/q mod p >1 y = gx mod p, {p, q, g, y} are public value and {x} is user’s private key r = (gk mod p) mod q m, r, s s =[k-1(H(m)+xr)] mod q a = (s’)-1 mod q, u 1 = [H(m’)a] mod q, u 2 = (r’a) mod q b = [(gu 1* yu 2) mod p] mod q If b = r’, the signature is verified Bob

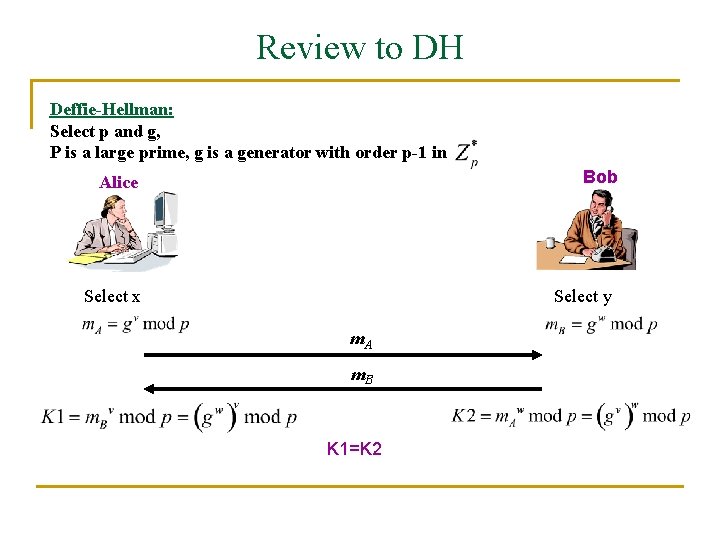
Review to DH Deffie-Hellman: Select p and g, P is a large prime, g is a generator with order p-1 in Bob Alice Select x Select y m. A m. B K 1=K 2

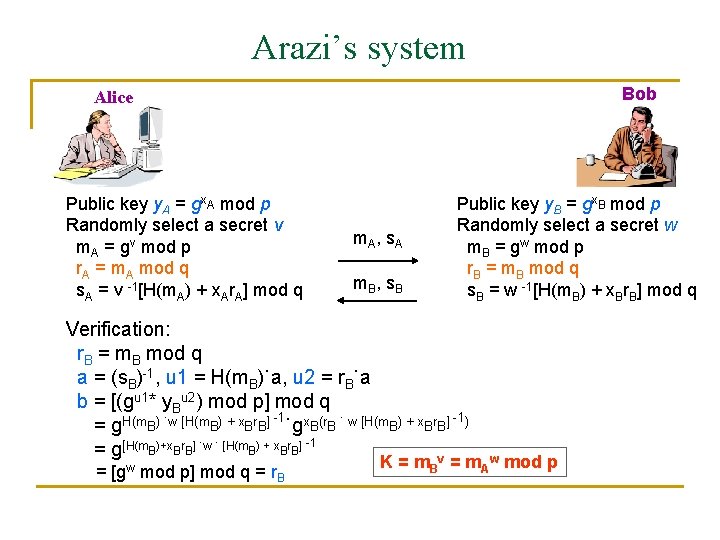
Arazi’s system Bob Alice Public key y. A = gx. A mod p Randomly select a secret v m. A = gv mod p r. A = m. A mod q s. A = v -1[H(m. A) + x. Ar. A] mod q m. A, s. A m. B, s. B Public key y. B = gx. B mod p Randomly select a secret w m. B = gw mod p r. B = m. B mod q s. B = w -1[H(m. B) + x. Br. B] mod q Verification: r. B = m. B mod q a = (s. B)-1, u 1 = H(m. B)˙a, u 2 = r. B˙a b = [(gu 1* y. Bu 2) mod p] mod q = g. H(m. B) ˙w [H(m. B) + x. Br. B] -1˙gx. B(r. B ˙ w [H(m. B) + x. Br. B] -1) = g[H(m. B)+x. Br. B] ˙w ˙ [H(m. B) + x. Br. B] -1 v = [gw mod p] mod q = r. B K = m. B = m. Aw mod p

Known key attack (Nyberg et al. 1994) Except K and gx. Ax. B mod p, all quantities are publicly known If K is know, gx. Ax. B mod p can be easily computed and vice versa

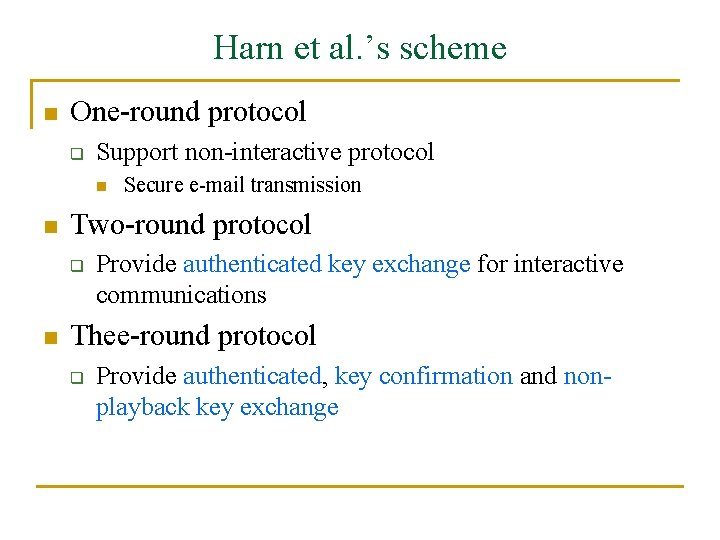
Harn et al. ’s scheme n One-round protocol q Support non-interactive protocol n n Two-round protocol q n Secure e-mail transmission Provide authenticated key exchange for interactive communications Thee-round protocol q Provide authenticated, key confirmation and nonplayback key exchange

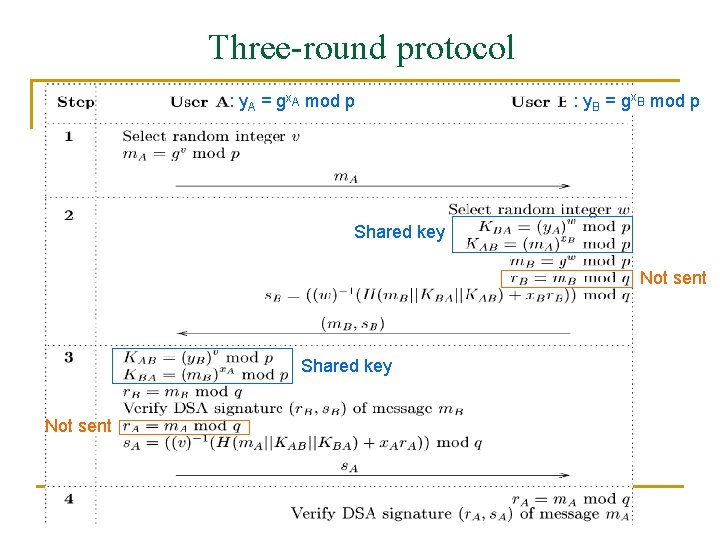
Three-round protocol : y. A = gx. A mod p : y. B = gx. B mod p Shared key Not sent

Security analysis (known key attack 1/2)

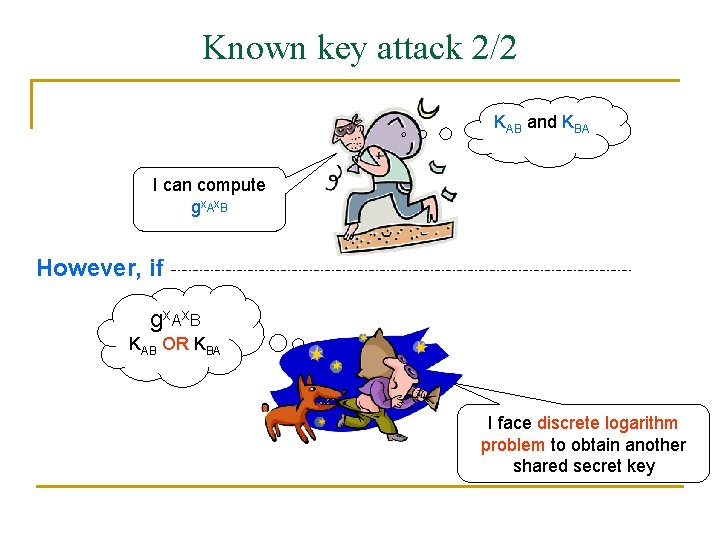
Known key attack 2/2 KAB and KBA I can compute gx. Ax. B However, if gx. Ax. B KAB OR KBA I face discrete logarithm problem to obtain another shared secret key

Summary of contribution n Provide multiple secret keys, one for each direction q n The shared key is included in the signature equation q n Conforms with most standard protocols, e. g. SSL and IPSec Prevent known key attack and key replay attack Three-round protocol achieves key confirmation q Prevent unknown key-share attack