Integrated Math Section 3 5 Functions and Relations
















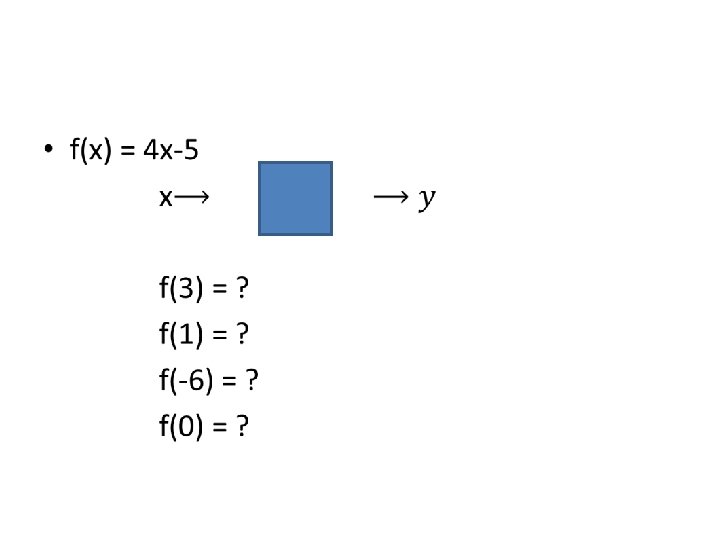
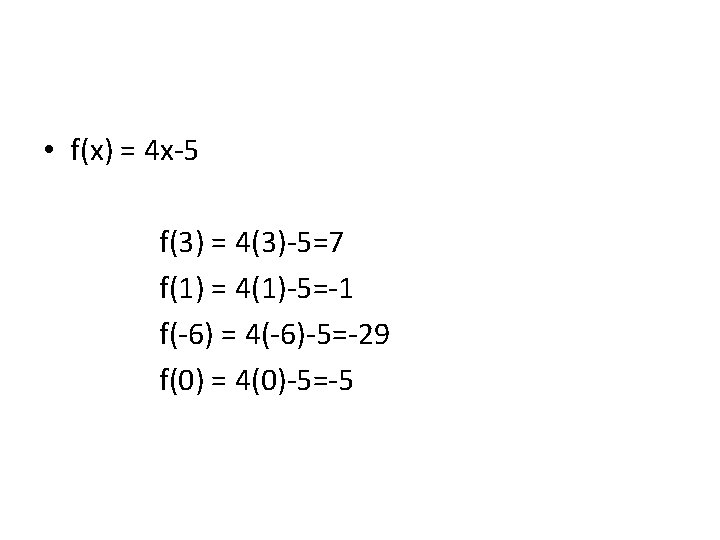



- Slides: 29

Integrated Math Section 3. 5 Functions and Relations

• Recall the definitions for a linear function, independent variable and dependent variable.

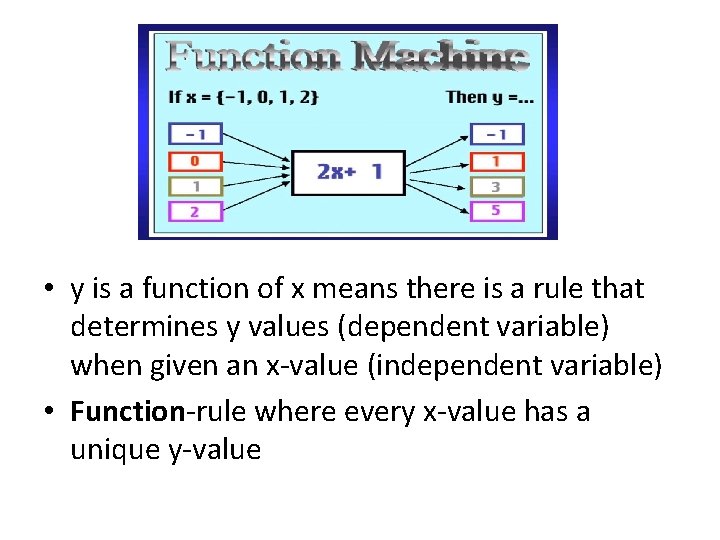
• y is a function of x means there is a rule that determines y values (dependent variable) when given an x-value (independent variable) • Function-rule where every x-value has a unique y-value

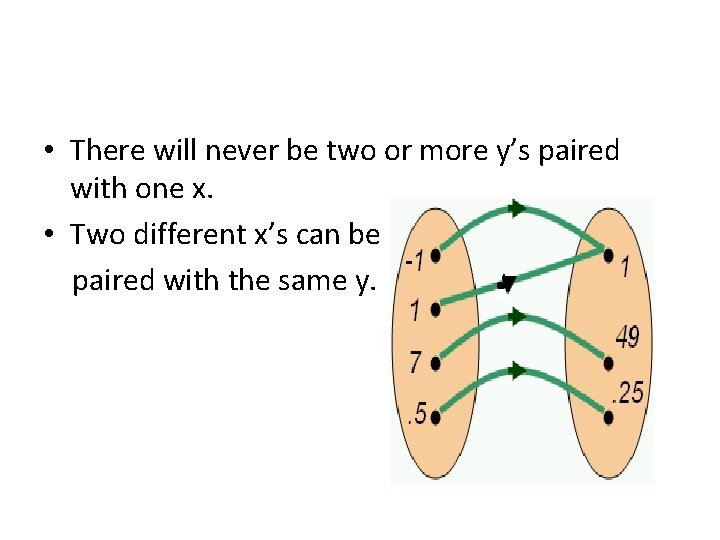
• You might put two different numbers in and get the same y coming out • You will NEVER put a number (x) in a function and get two numbers (y) out!!!

• There will never be two or more y’s paired with one x. • Two different x’s can be paired with the same y.

Which would be a function? • Scenario #1 Let x= student school ID number Let y= student’s last score on a math test • Scenario #2 Let x= a test score Let y=student ID numbers with a given score

• http: //www. youtube. com/watch? v=s. E 4 eq 0 cj. L Fk

Try these! • Pg. 206 #2, #4

• http: //www. youtube. com/watch? v=ilhb. Oiety q. A

Writing a function •

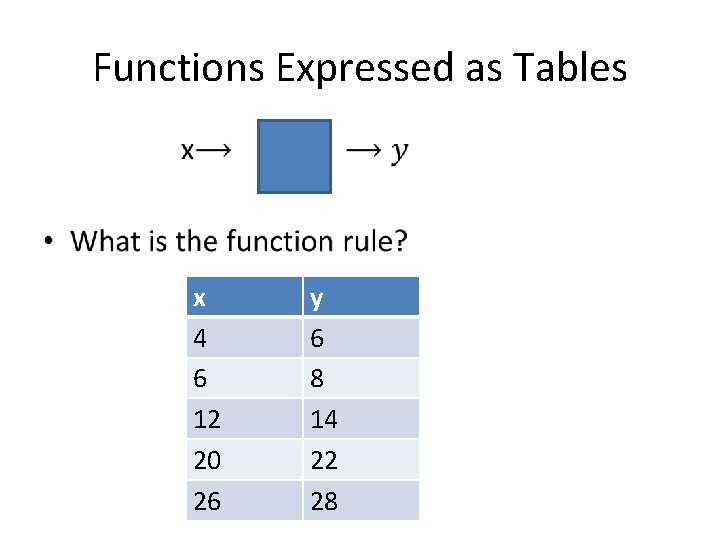
Functions Expressed as Tables • x 4 6 12 20 26 y 6 8 14 22 28

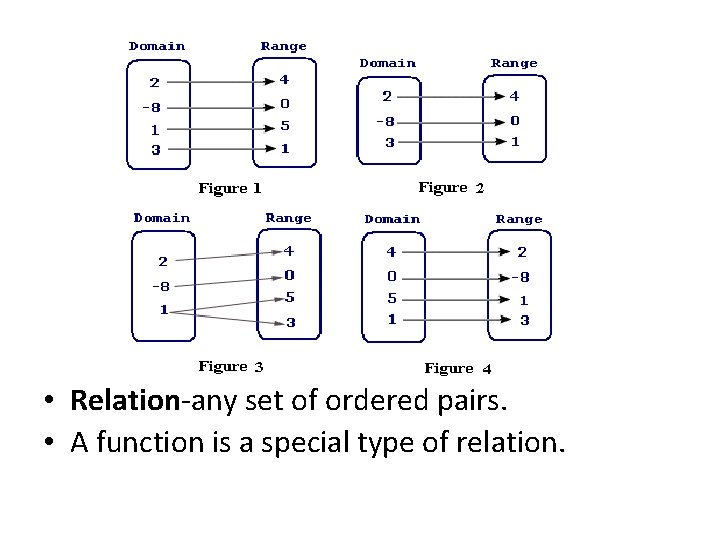
• Relation-any set of ordered pairs. • A function is a special type of relation.

• When given a set of ordered pairs, the relation is a function if no x value is repeated with different y’s. #1 { (4, 6) (2, 8) (2, 5) } #2 { (7, 3) (7, 1) (12, 15) } #3 { (6, 5) (8, 5) (10, 17) }

https: //www. youtube. com/watch? v=VUTXs. PFxq. Q

Assignment #15 A Pg. 206 #1 -33 odd

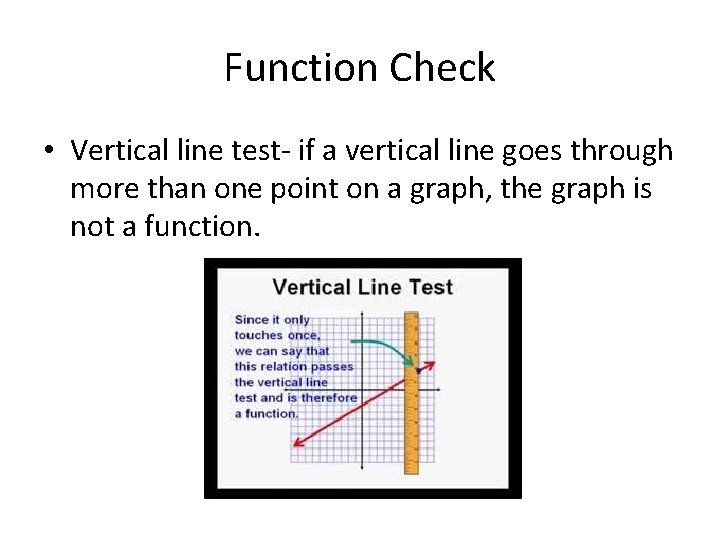
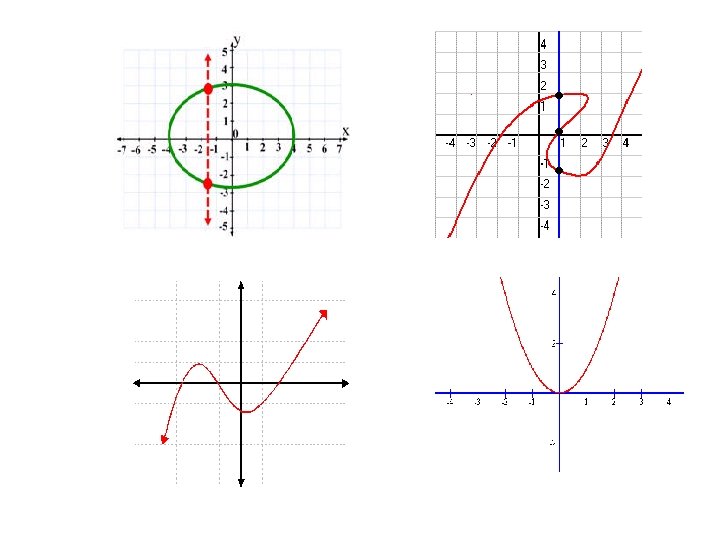
• When you look at a graph if any vertical line crosses more than one point, you don’t have a function!

Function Check • Vertical line test- if a vertical line goes through more than one point on a graph, the graph is not a function.

• Function • Not function


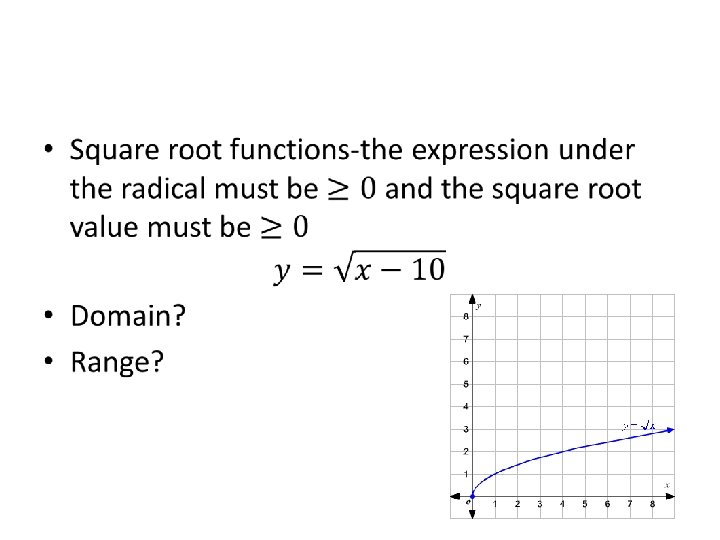
• • • Domain- set of input (x) values (independent) Range- set of output (y) values (dependent) For ordered pairs{(2, 8) (3, 9) (4, 10) (5, 10)} Domain {2, 3, 4, 5} Range {8, 9, 10}

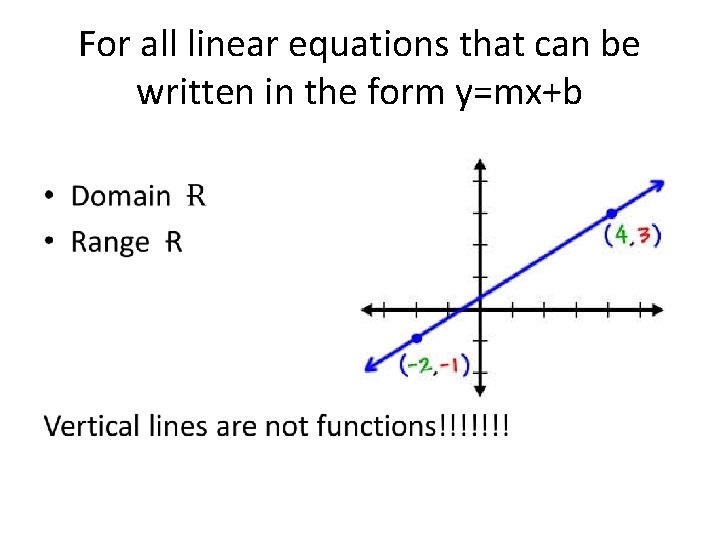
For all linear equations that can be written in the form y=mx+b •


Group work! Pg 208 #70 -80 even

Function notation • Read f(x) as “f of x” y= 2 x+5 can be written as f(x)=2 x+5 • When there is a number in the parentheses, you are given the input value f(3) is asking for the output value when 3 is the input value.
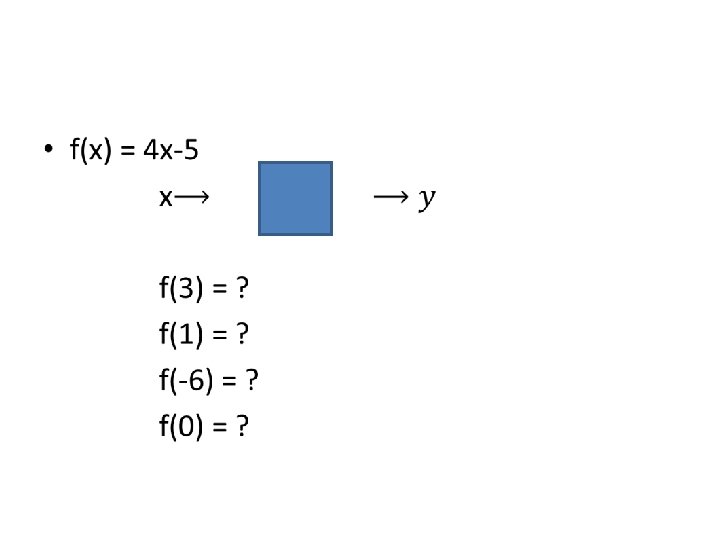
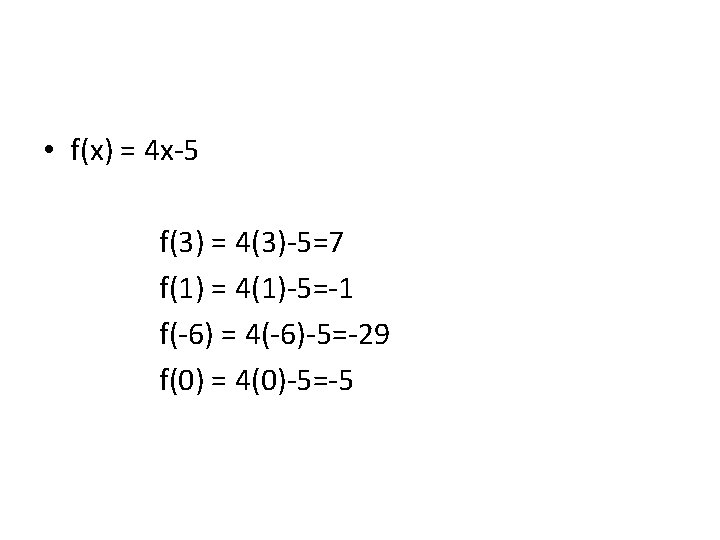
• f(x) = 4 x-5 f(3) = 4(3)-5=7 f(1) = 4(1)-5=-1 f(-6) = 4(-6)-5=-29 f(0) = 4(0)-5=-5

Group Work! Pg. 208 #82 -94 even

Look at #102 on page 208 Two steps #1 Write a function #2 Find P(40)

Assignment #15 B • Pg. 207 #63 -79 odd, #81 -103 odd