Integrated Math Section 2 1 Linear Equations in

Definitions • Equation- sentence that has two expressions joined by an equal sign. •

• When a value is entered into an equation, it will make a

Checking a value! #1 Write the equation #2 Plug in the value #3 Do

Properties of Equality What you do to one side of the equation, you must

• Make a line down from the equal sign. Now you have two

• Crossing some lines can be highly dangerous!

Steps to Solve an Equation (find the variable) Step #1 Draw a line down

• Solve an equation means finding the variable.

• Steps #2 and #3 can be summed up by saying SIMPLIFY EACH

• At this point, you should have a maximum of two terms per

$Equations with Fractions • You can work with fractions Or • You can multiply$

• “The magic number” is the LCM (least common multiple) of all the

Words you might see • Identity- an equation that has all real numbers as

Successful solving • Be very neat! • Show all work! • Write a complete

This is the pattern! • • Simplify then Do something, do something Write a

• Always write the whole equation! • NO SCRAPS!

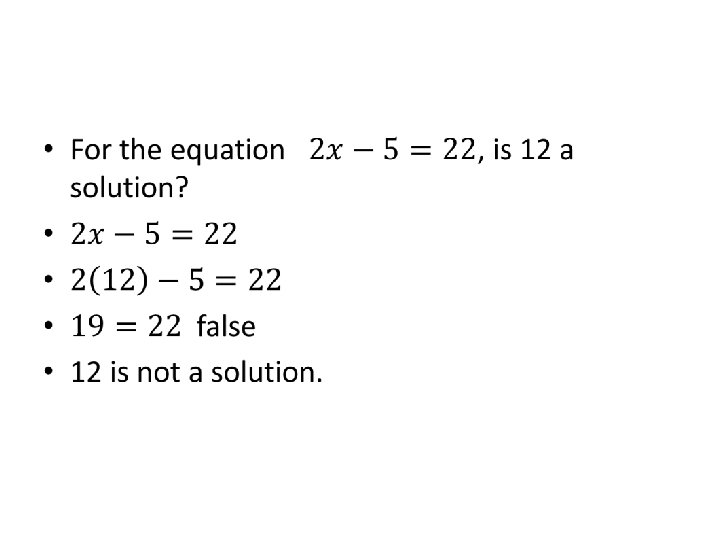
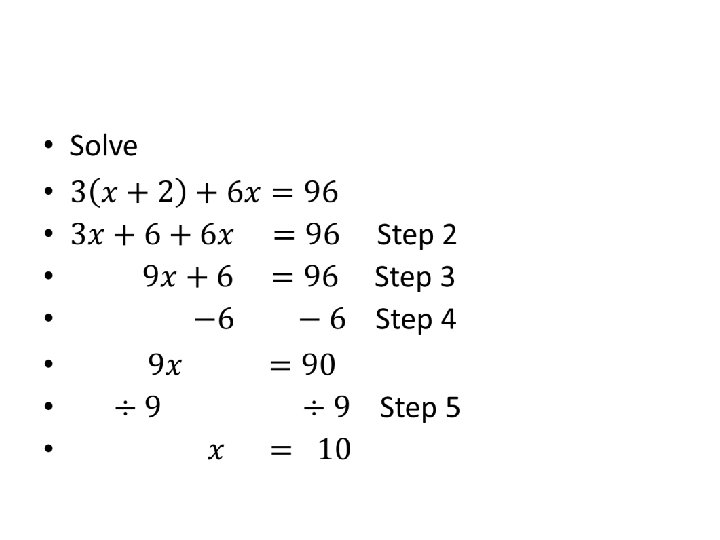
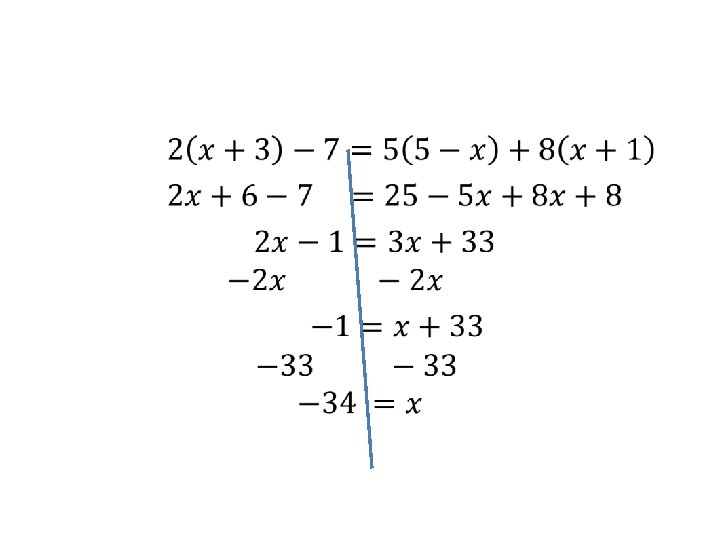
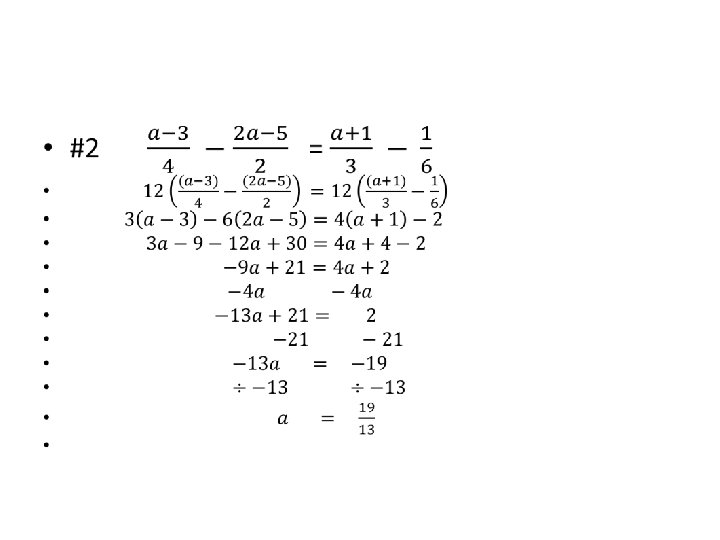
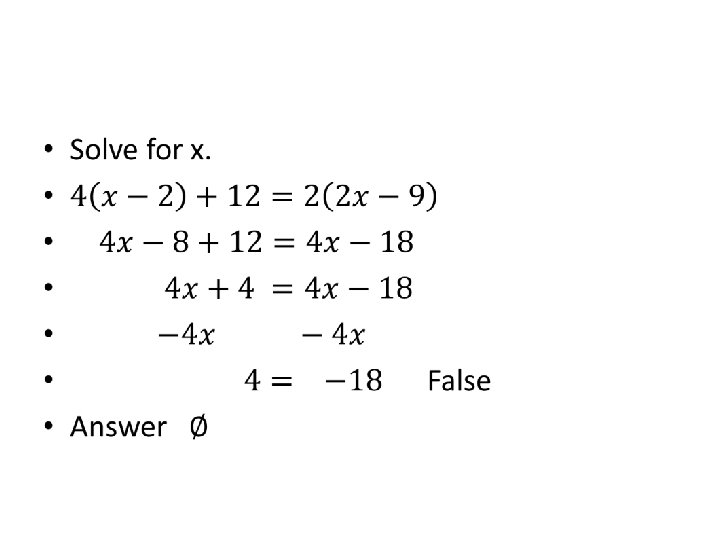
Slides: 28

Download presentation

Integrated Math Section 2. 1 Linear Equations in One Variable

Definitions • Equation- sentence that has two expressions joined by an equal sign. • Solution set- set of all solutions that satisfy the equation. • Solve- find the solution set to an equation • Equivalent equations- equations that have the same solution set

• When a value is entered into an equation, it will make a true statement or a false statement.

Checking a value! #1 Write the equation #2 Plug in the value #3 Do the math on both sides of the equation! True statement? Value works. False statement? Value does not work.

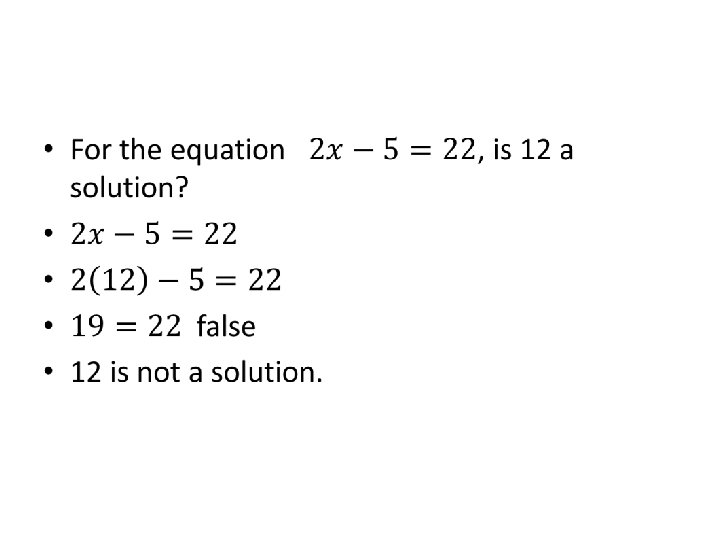
Properties of Equality What you do to one side of the equation, you must do to the other side. • This applies to adding or multiplying. • Recall subtracting and dividing can be turned into adding and multiplying problems.

• Make a line down from the equal sign. Now you have two sides. • Keep them equal when solving!!!

• Crossing some lines can be highly dangerous!

Steps to Solve an Equation (find the variable) Step #1 Draw a line down from the equal sign. Step #2 Eliminate all parentheses (if necessary) using distributive property Step #3 Combine (like terms) –on the same side of the line

• Solve an equation means finding the variable.

• Steps #2 and #3 can be summed up by saying SIMPLIFY EACH SIDE OF THE EQUATION!

• At this point, you should have a maximum of two terms per side. Step #4 Use addition or subtraction to get all the variable terms on one side and all numbers on the other side Step #5 Use division or multiplication to create a coefficient of one in front of the variable

The Zukowski Way

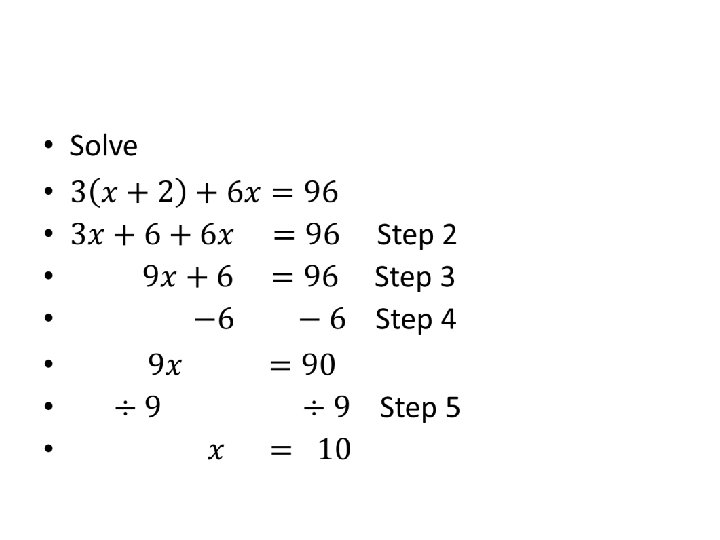
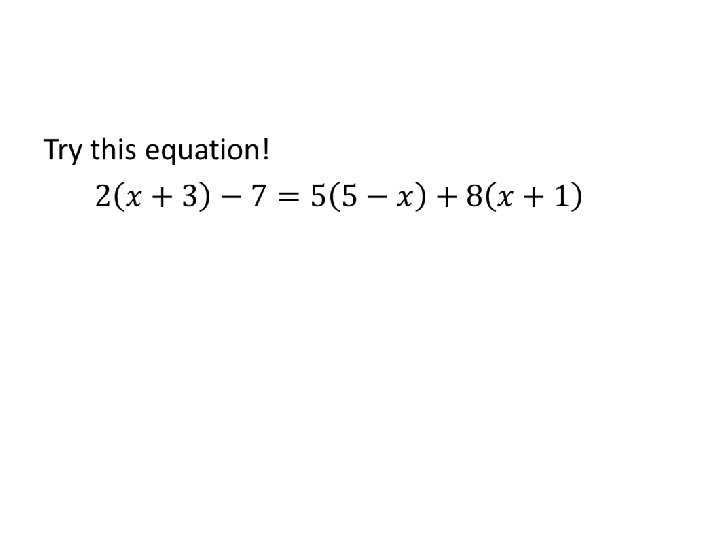
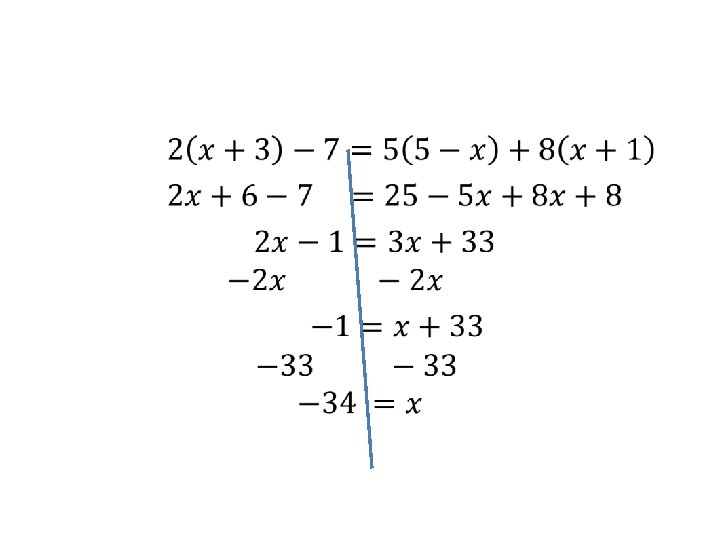
Assignment #7 A • Pg. 75 #1 -23 odd

$Equations with Fractions • You can work with fractions Or • You can multiply$

Equations with Fractions • You can work with fractions Or • You can multiply both sides of the equation by “the magic number” that will eliminate all the fractions.

• “The magic number” is the LCM (least common multiple) of all the denominators!

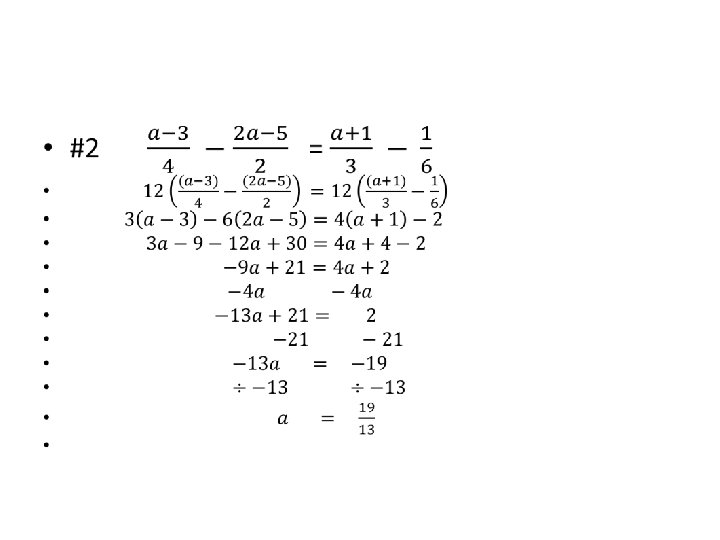
Special Cases •

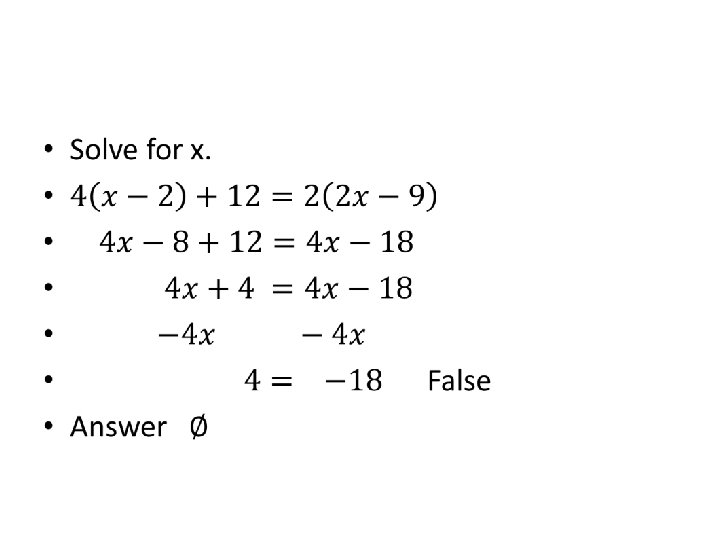
Words you might see • Identity- an equation that has all real numbers as solutions • Conditional equation- an equation that has a solution but not all real numbers • Inconsistent equation- an equation that has no solutions

Successful solving • Be very neat! • Show all work! • Write a complete equation on each line! • Work down your paper!

This is the pattern! • • Simplify then Do something, do something Write a new equation … until the variable is all by itself!

• Always write the whole equation! • NO SCRAPS!