Integrali Le primitive di una funzione Diciamo che

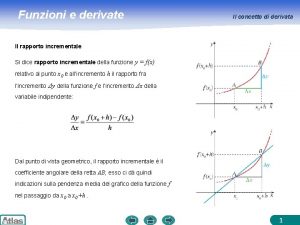
Integrali Le primitive di una funzione Diciamo che una funzione se è una primitiva di un’altra funzione in un dato intervallo in ogni punto di Per esempio: se allora perché 1

Integrali Ogni funzione L’integrale indefinito ha infinite primitive che differiscono tra loro per una costante; relativamente ai precedenti esempi: se tutte le primitive sono con c costante reale. L’insieme di tutte le primitive di una funzione si dice integrale indefinito di e si indica con il simbolo: 2

Integrali L’integrale indefinito ESEMPI 1) L’insieme delle primitive della funzione è: perché 2) L’insieme delle primitive della funzione è: perché 3

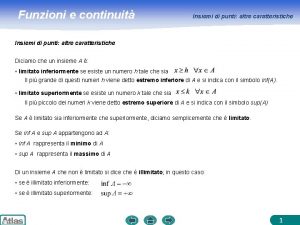
Integrali L’integrale indefinito Per trovare l’integrale indefinito delle funzioni elementari dobbiamo in un certo senso invertire le regole di derivazione. Ricordiamo le primitive di alcune tra le principali funzioni. 4

Integrali L’integrale indefinito ESEMPI 1) 2) 3) 4) 5

Integrali I metodi di integrazione Le prime proprietà dell’integrale indefinito e il metodo di scomposizione. L’integrale del prodotto di una funzione per una costante è uguale al prodotto della costante per l’integrale della funzione. In simboli L’integrale della somma algebrica di due o più funzioni è uguale alla somma algebrica degli integrali delle singole funzioni. In simboli Queste due proprietà ci dicono che l’integrale indefinito è un operatore lineare, cioè: 6

Integrali I metodi di integrazione Il metodo di integrazione che sfrutta le precedenti proprietà prende il nome di metodo di scomposizione. ESEMPI 1. 2. 3. 7

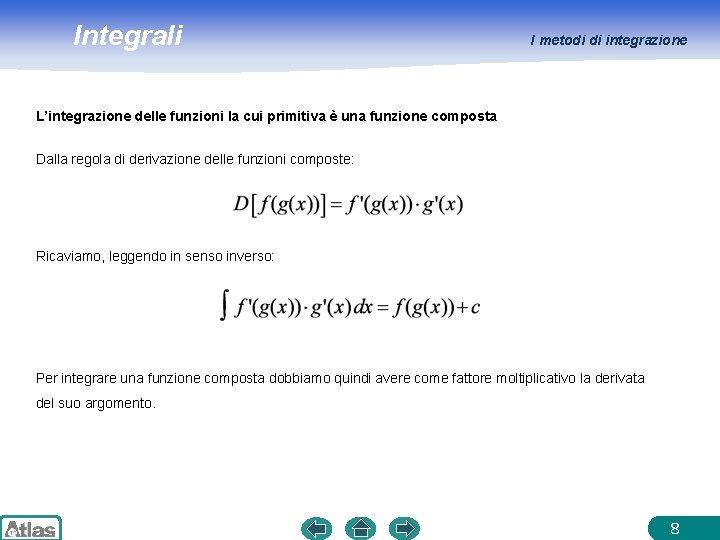
Integrali I metodi di integrazione L’integrazione delle funzioni la cui primitiva è una funzione composta Dalla regola di derivazione delle funzioni composte: Ricaviamo, leggendo in senso inverso: Per integrare una funzione composta dobbiamo quindi avere come fattore moltiplicativo la derivata del suo argomento. 8

Integrali I metodi di integrazione ESEMPIO è la funzione potenza è il cui argomento è , la derivata di . Possiamo quindi applicare la regola: Infatti: cioè 9

Integrali I metodi di integrazione ALTRI ESEMPI 1. Utilizziamo la regola di integrazione della potenza: dove e 10

Integrali I metodi di integrazione 2. Dobbiamo riferirci alla regola di integrazione di dove Per avere e dobbiamo moltiplicare, e quindi dividere per 2: 11

Integrali I metodi di integrazione ALCUNI CASI PARTICOLARI Per procedere più velocemente nel calcolo degli integrali indefiniti conviene ricordare le seguenti regole, che si deducono da quelle di integrazione delle funzioni composte: essendo k=3 essendo k=5 otteniamo 12

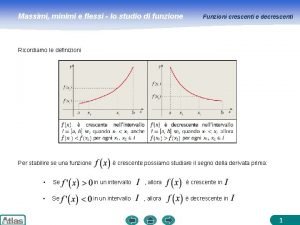
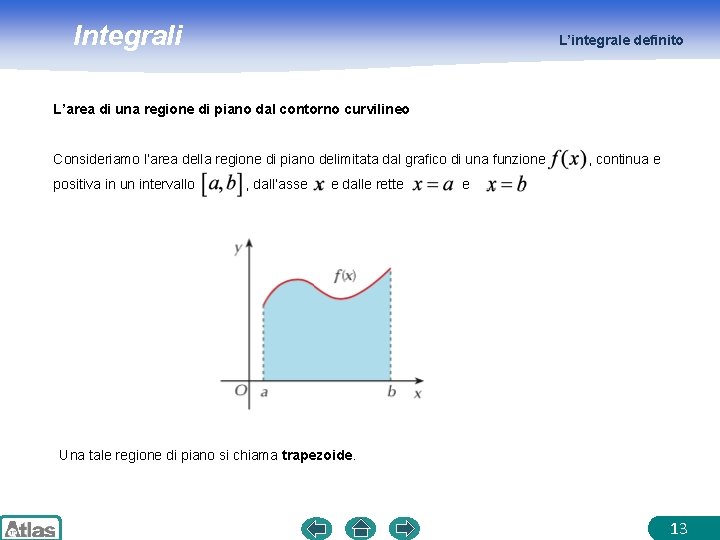
Integrali L’integrale definito L’area di una regione di piano dal contorno curvilineo Consideriamo l’area della regione di piano delimitata dal grafico di una funzione positiva in un intervallo , dall’asse e dalle rette , continua e e Una tale regione di piano si chiama trapezoide. 13

Integrali L’integrale definito Per calcolare l’area di un trapezoide suddividiamo l’intervallo in parti uguali di ampiezza . Le altezze dei rettangoli sono i valori assunti dalla funzione in opportuni punti . Un valore approssimato dell’area del trapezoide è quindi dato da: Al crescere di il valore della sommatoria approssima sempre meglio l’area del trapezoide. Possiamo quindi assumere che sia: Area del trapezoide = Questo limite viene indicato con il simbolo che prende il nome di integrale definito tra a e b di f(x) 14

Integrali L’integrale definito Le proprietà dell’integrale definito • Cioè, se gli estremi di integrazione sono uguali, l’integrale definito è nullo. • Cioè, scambiando gli estremi di integrazione, l’integrale definito cambia segno. • Proprietà di linearità con 15

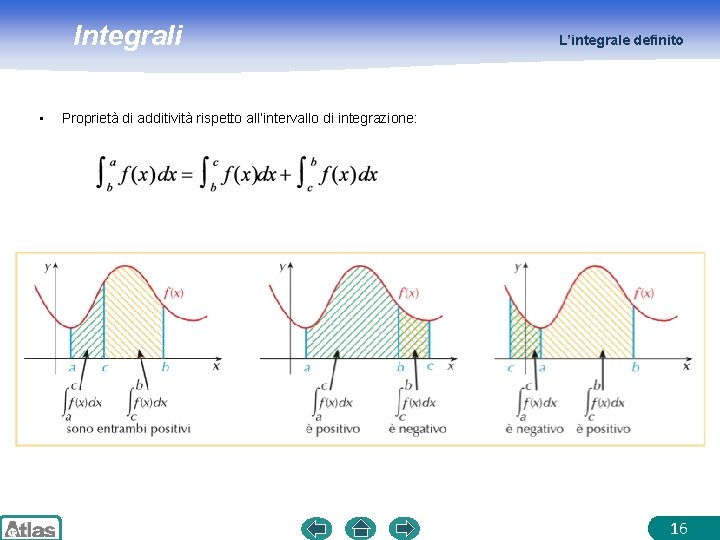
Integrali • L’integrale definito Proprietà di additività rispetto all’intervallo di integrazione: 16

Integrali Il calcolo di un integrale definito Le funzioni integrale Se è una funzione continua in un intervallo valutare l’integrale definito della funzione variabile in tra , possiamo e un punto . In questo modo: (t sostituisce x per evitare confusioni) diventa una funzione che rappresenta l’area del trapezoide tra a e x. A questa funzione si dà il nome di funzione integrale. 17

Integrali Il calcolo di un integrale definito Il teorema fondamentale del calcolo integrale La funzione integrale gode di un’importante proprietà: La sua derivata coincide con la funzione Di conseguenza, la funzione integrale diventa una primitiva della funzione . 18

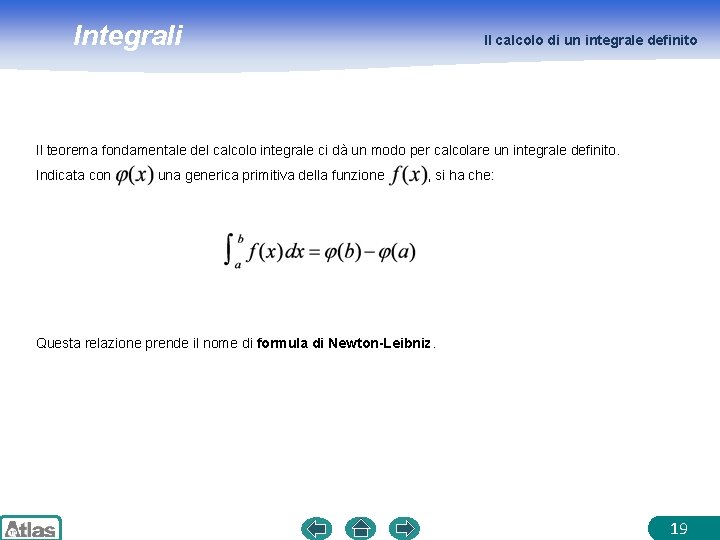
Integrali Il calcolo di un integrale definito Il teorema fondamentale del calcolo integrale ci dà un modo per calcolare un integrale definito. Indicata con una generica primitiva della funzione , si ha che: Questa relazione prende il nome di formula di Newton-Leibniz. 19

Integrali Il calcolo di un integrale definito ESEMPI 1. Calcoliamo Troviamo una primitiva della funzione : quindi In definitiva: Poiché la costante c è ininfluente per il calcolo dell’integrale, possiamo ometterla nella scrittura della primitiva. 2. Calcoliamo 20

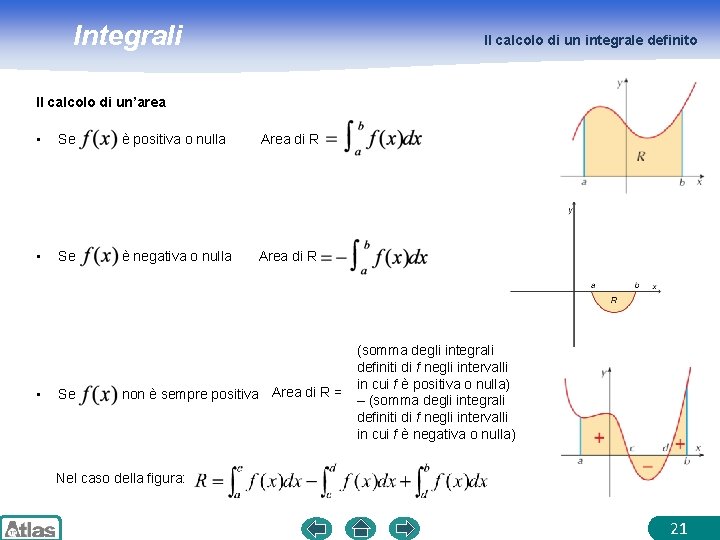
Integrali Il calcolo di un integrale definito Il calcolo di un’area • Se è positiva o nulla Area di R • Se è negativa o nulla Area di R • Se non è sempre positiva Area di R = (somma degli integrali definiti di f negli intervalli in cui f è positiva o nulla) – (somma degli integrali definiti di f negli intervalli in cui f è negativa o nulla) Nel caso della figura: 21

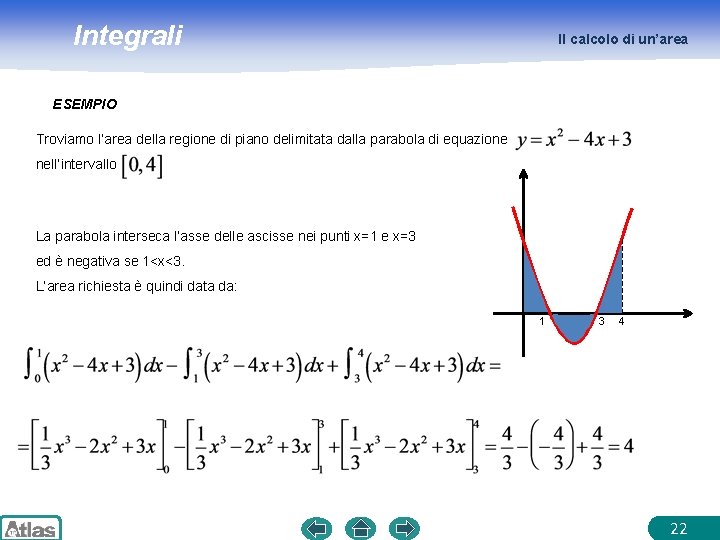
Integrali Il calcolo di un’area ESEMPIO Troviamo l’area della regione di piano delimitata dalla parabola di equazione nell’intervallo La parabola interseca l’asse delle ascisse nei punti x=1 e x=3 ed è negativa se 1<x<3. L’area richiesta è quindi data da: 1 3 4 22

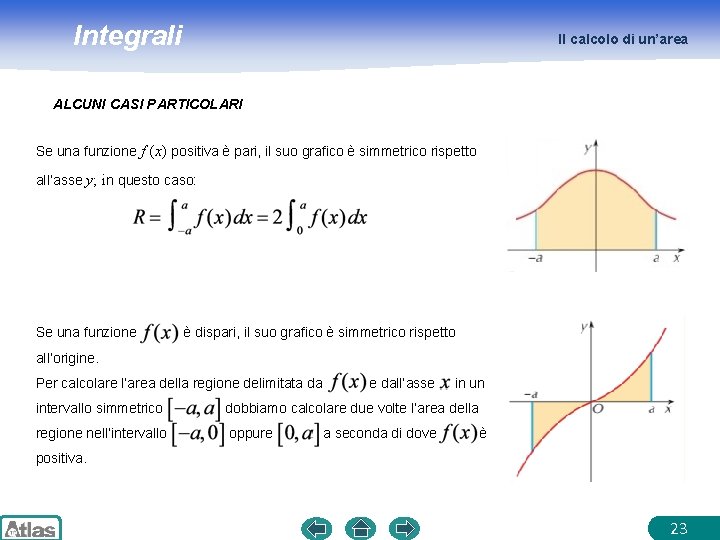
Integrali Il calcolo di un’area ALCUNI CASI PARTICOLARI Se una funzione f (x) positiva è pari, il suo grafico è simmetrico rispetto all’asse y; in questo caso: Se una funzione è dispari, il suo grafico è simmetrico rispetto all’origine. Per calcolare l’area della regione delimitata da e dall’asse in un intervallo simmetrico dobbiamo calcolare due volte l’area della regione nell’intervallo oppure a seconda di dove è positiva. 23

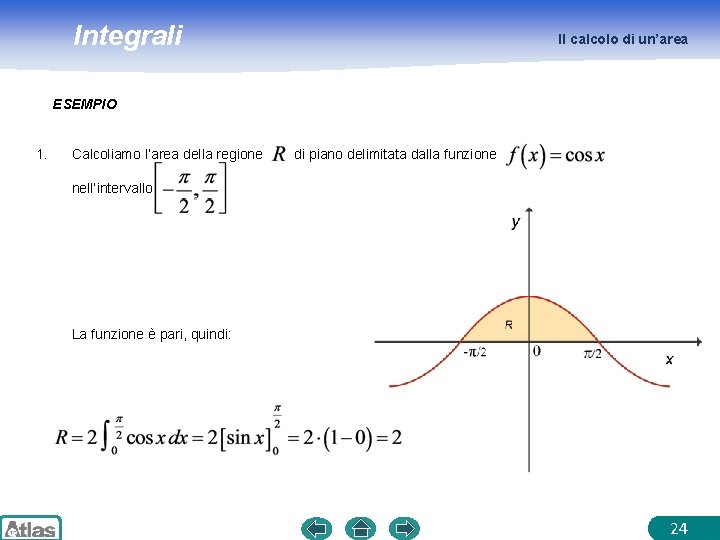
Integrali Il calcolo di un’area ESEMPIO 1. Calcoliamo l’area della regione di piano delimitata dalla funzione nell’intervallo La funzione è pari, quindi: 24