Integral Transform Integral Transforms Integral transform K t

Integral Transform

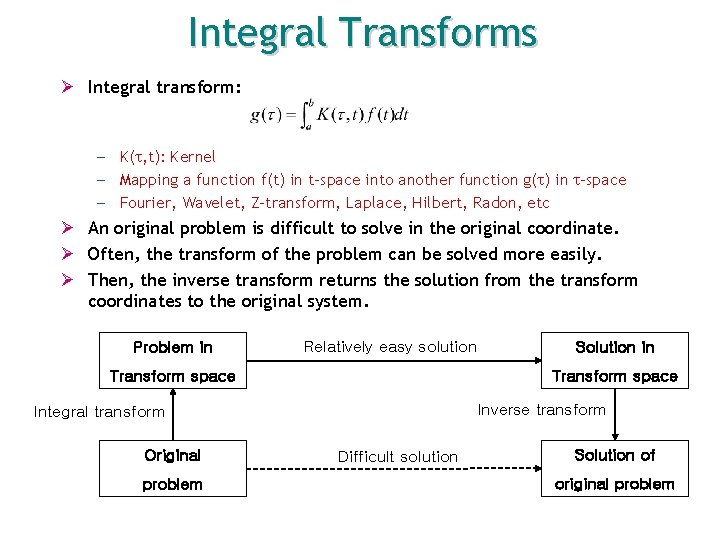
Integral Transforms Ø Integral transform: – K( , t): Kernel – Mapping a function f(t) in t-space into another function g( ) in -space – Fourier, Wavelet, Z-transform, Laplace, Hilbert, Radon, etc Ø An original problem is difficult to solve in the original coordinate. Ø Often, the transform of the problem can be solved more easily. Ø Then, the inverse transform returns the solution from the transform coordinates to the original system. Problem in Relatively easy solution Transform space Inverse transform Integral transform Original problem Solution in Difficult solution Solution of original problem

Fourier Transform, I Ø A physical process can be described either in the time domain by a function of time t, h(t), or in the frequency domain as a function of frequency f, H(f) Ø h(t) and H(f) are two different representations of the same process. Ø One goes back and forth between these two representations by means of the Fourier transform, – Dirac delta function: Ø Using angular frequency =2 f,

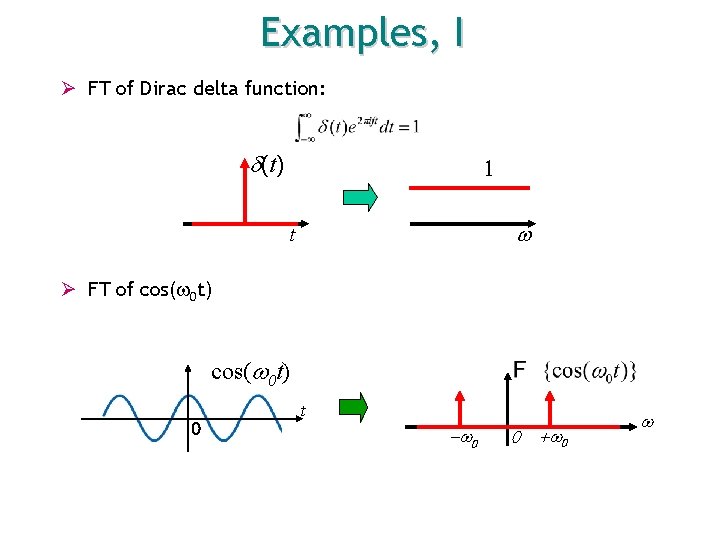
Examples, I Ø FT of Dirac delta function: d(t) 1 w t Ø FT of cos( 0 t) cos(w 0 t) 0 t -w 0 0 +w 0 w

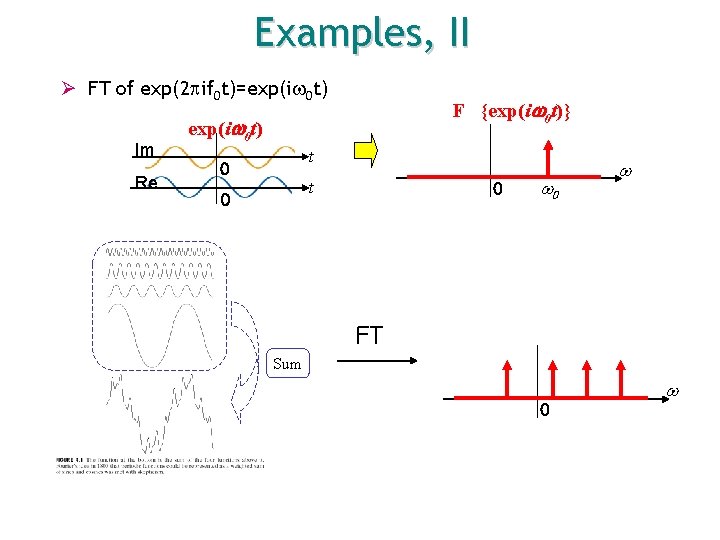
Examples, II Ø FT of exp(2 if 0 t)=exp(i 0 t) Im Re F {exp(iw 0 t)} exp(iw 0 t) t 0 0 t 0 w FT Sum 0 w

Fast Fourier Transform (FFT), I Ø DFT appears to be an O(N 2) process. Ø Danielson and Lanczos; DFT of length N can be rewritten as the sum of two DFT of length N/2. Ø We can do the same reduction of Hk 0 to the transform of its N/4 evennumbered input data and N/4 odd-numbered data. Ø For N = 2 R, we can continue applying the reduction until we subdivide the data into the transforms of length 1. Ø For every pattern of log 2 N number of 0’s and 1’s, there is one-point transformation that is just one of the input number hn

Fast Fourier Transform (FFT), II Ø For N=8 Ø Since WN/2 = -1, Hk 0 and Hk 1 have period N/2, Ø Diagrammatically (butterfly), Ø There are N/2 butterflies for this stage of the FFT, and each butterfly requires one multiplication

Fast Fourier Transform (FFT), III Ø So far, Ø The splitting of {Hk} into two half-size DFTs can be repeated on Hk 0 and Hk 1 themselves,

Fast Fourier Transform (FFT), III Ø So far, – – – {Hk 00} is the N/4 -point DFT of {h 0, h 4, …, h. N-4}, {Hk 01} is the N/4 -point DFT of {h 2, h 6, …, h. N-2}, {Hk 10} is the N/4 -point DFT of {h 1, h 5, …, h. N-3}, {Hk 11} is the N/4 -point DFT of {h 3, h 7, …, h. N-1}, Note that there is a reversal of the last two digits in the binary expansions of the indices j in {hj}.

Fast Fourier Transform (FFT), IV

Fast Fourier Transform (FFT), V Ø If we continue with this process of halving the order of the DFTS, then after R=log 2 N stages, we reach where we are performing N one-point DFTs. – One-point DFT of the number hj is just the identity hj – Since the reversal of the order of the bits will continue, all bits in the binary expansion of j will be arranged in reverse order. – Therefore, to begin the FFT, one must first rearrange {hj} so it is listed in bit reverse order. Ø For each of the log 2 N stages, there are N/2 multiplications, hence there are (N/2)log 2 N multiplications needed for FFT. – Much less time than the (N-1)2 multiplications needed for a direct DFT calculation. – When N=1024, FFT=5120 multiplication, DFT=1, 046, 529 savings by a factor of almost 200.

Fast Fourier Transform (FFT), VI