INTEGRAL GARIS Di dalam integral Garis kita akan



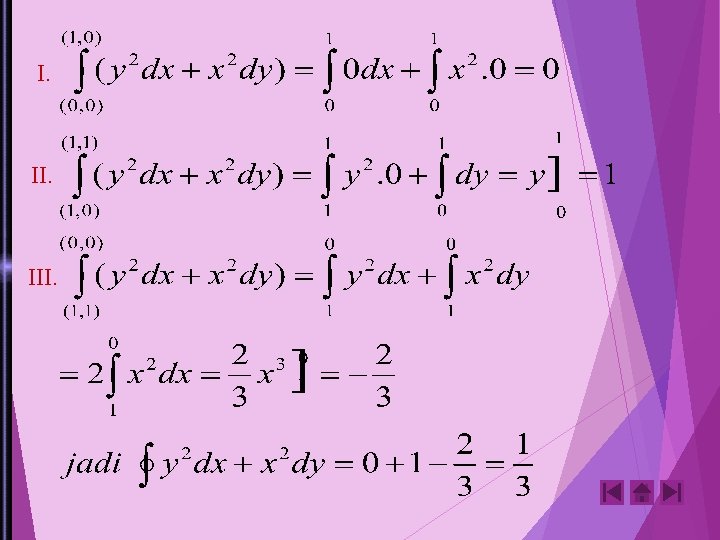



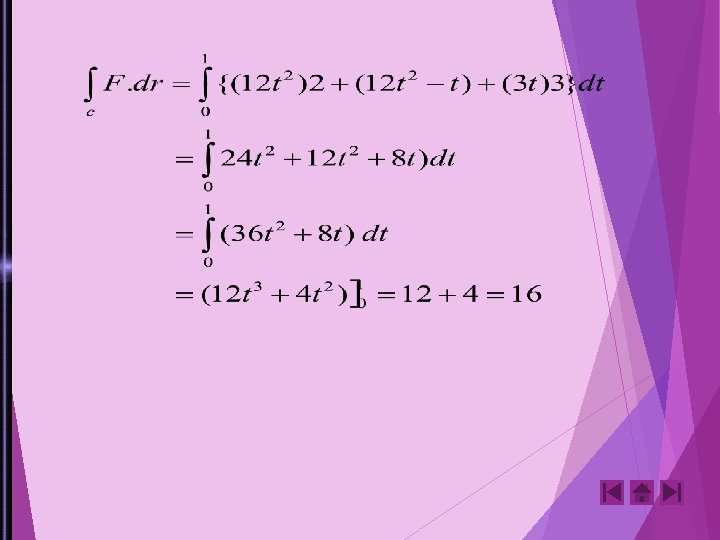
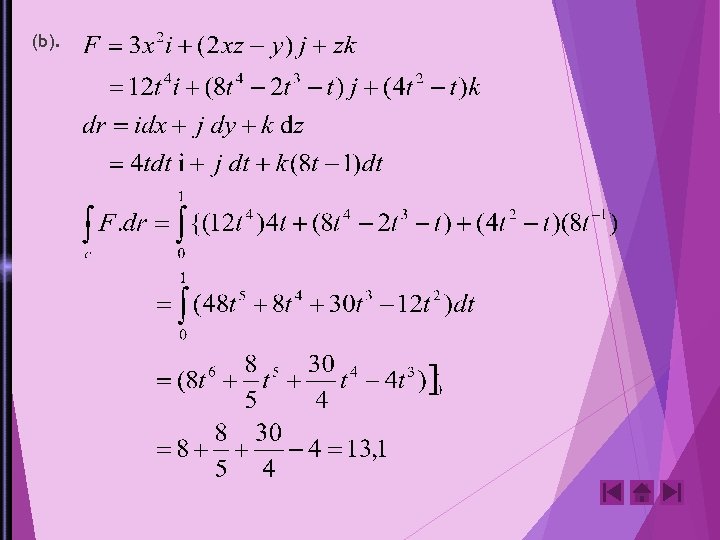
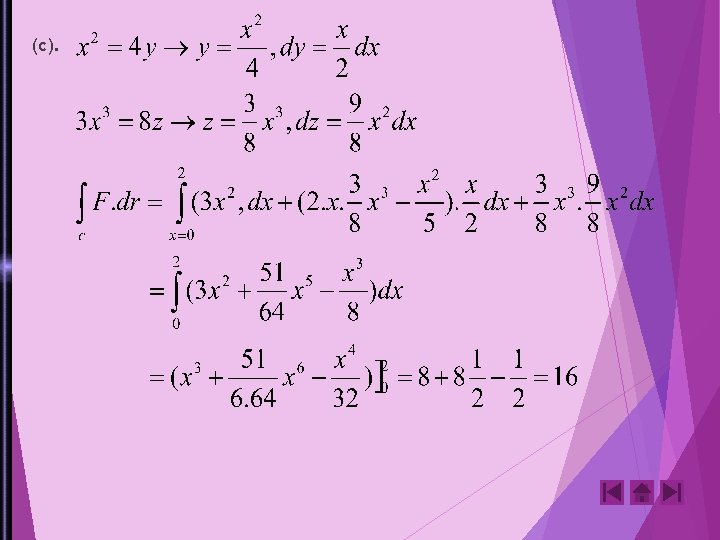








- Slides: 18

INTEGRAL GARIS Di dalam integral Garis kita akan mengintegralkan sepanjang kurva C di dalam ruang (Bidang) dan yang di Integralkan akan merupakan fungsi yang terdefinisi pada setiap sisi dari C. Integral Garis yang lazim adalah panjang Busur, yang dinyatakan dengan : Jika C adalah kurva tertutup (kurva yang memotong dirinya sendiri), maka integral mengelilingi C yang sering ditunjukkan oleh:

Contoh : 1. Hitunglah (xy 2 dx + x 2 y dy), dengan C adalah Busur Parabola y = x 2 dari ( -1, 1) sampai (0, 0) Jawab: (xy 2 dx + x 2 y dy) : = = =

2. Hitunglah , dengan C adalah segitiga dengan ujung-ujung (1, 0), (1, 1) dan (0, 0) Jawab: sebagai parameter dapat digunakan variabel X, integral C terdiri atas 3 potong garis sehingga. Membentuk 3 integral, yaitu = y y=x III (0, 0) (1, 1) y=x dy=dx II I (1, 0) x
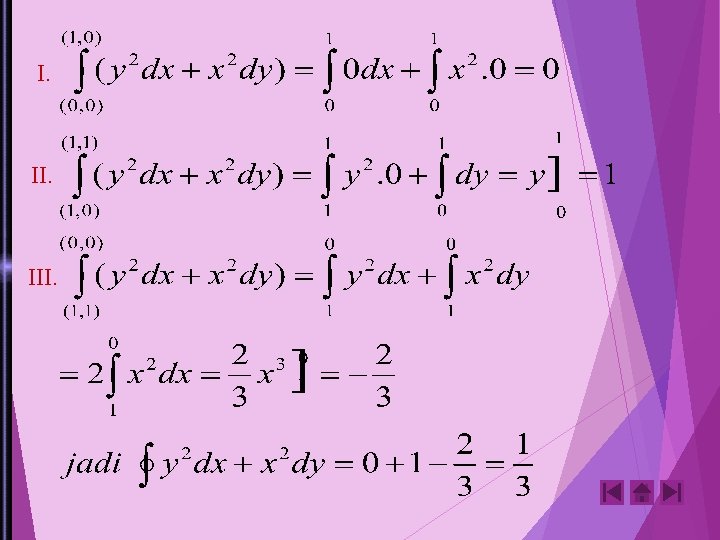
I. III.

Integral Garis Sebagai Integral Vektor Mis. r(t)i + y(t)j + z(t)k, dimana r(t) adalah vektor posisi dari (x, y, z) mendefinisikan sebuah kurva yang menghubungkan titik-titik P 1 dan P 2. Mis. A(x, y, z) = A 1 i + A 2 j + A 3 k sebuah fungsi vektor dari posisi yang didefinisikan dan kontinu sepanjang C, maka integeral garis sepanjang C dan P 1 ke P 2, ditulis sebagai : Jika A adalah gaya F pada sebuah partikel yang bergerak sepanjang C, maka integeral garis ini menyatakan usaha yang dilakukan oleh gaya. Jika C adalah kurva tertutup, maka integeral yang mengelilingi C ditunjukan oleh :

Contoh: 1. Carilah usaha total yang dilakukan untuk menggerakan sebuah partikel dalam medan gaya yang diberikan oleh F = 3 xyi – 5 zj + 10 xk sepanjang kurva x = t 2 + 1, y = t 2, z = t 3 dari t = I hingga t = 2 Jawab : Usaha total = = 3 xy dx – 5 z dy + 10 x dz

2. Carilah usaha yang dilakukan dalam menggerakkan sebuah partikel dalam medan gaya F=3 x 2 i+(2 xz-y)j+zk sepanjang (a). Garis lurus (0, 0, 0) ke (2, 1, 3) (b). Kurva ruang x=2 t 2 , y=t , z=4 t 2 -t dari t=0 ke t=1 (c). Kurva yang didefinisikan oleh: x 2 = 4 y, 3 x 3 =8 z dari x=0 ke x=2 Jawab: (a). garis lurus yang menghubungkan (0, 0, 0) dan (2, 1, 3) dalam bentuk parameter diberikan oleh: x=2 t, y=t dan z=3 t F=3 x 2 i + (2 xz-y 2 j+zk =12 t 2 i+ (12 t 2 – t)j+3 z k dr=dx i+dy. j + d z k =(2 i + j + 3 k) dt
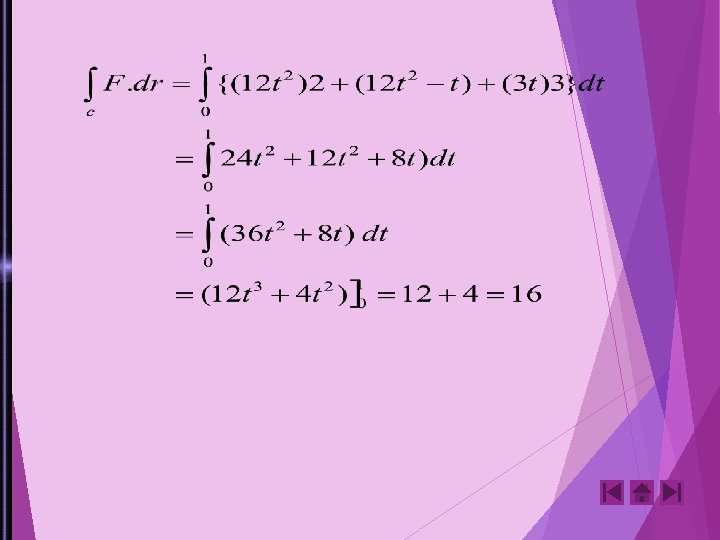
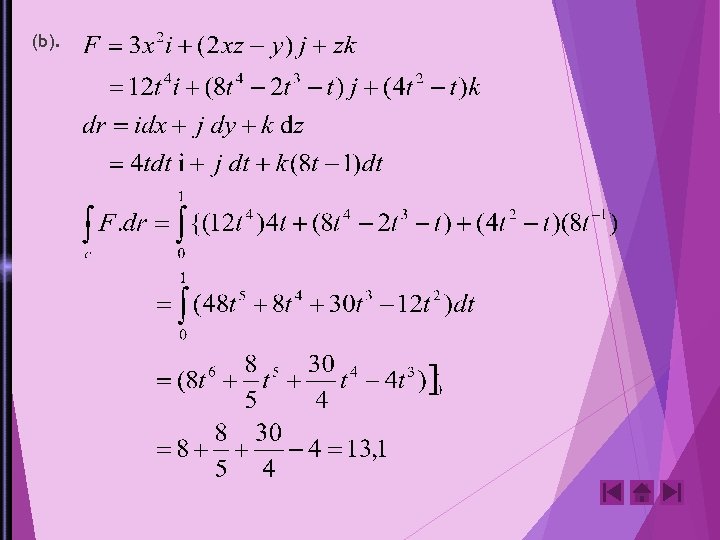
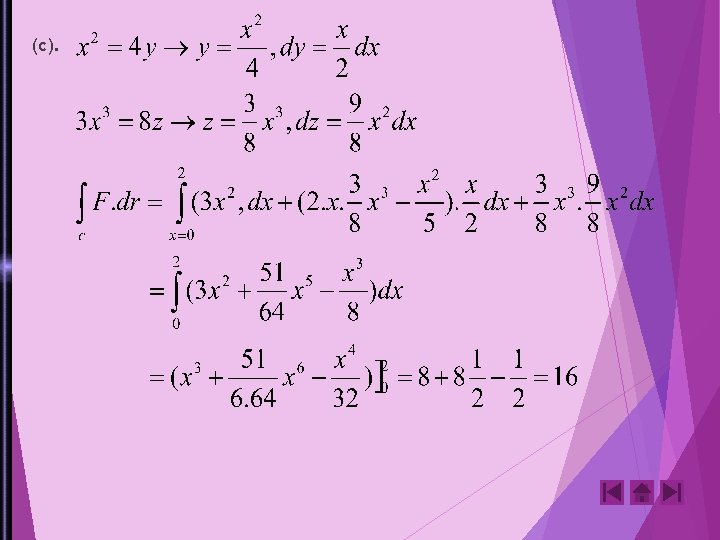

Ketidaktergantungan Integeral Garis Pada Lintasan Jika fungsi P(x, y, z) dan Q(x, y, z) dan R(x, y, z) didefinisikan dan kontinu dalam Domain D. Integeral garis P dx + Q dy + R dz dikatakan tidak tergantung pada lintasan di D, jika untuk setiap pasang titik – titik ujung A dan B di D, nilai integeral garisnya adalah : sama untuk semua lintasan C dari A dan B. Nilai integeral hanya tergantung pada pemilihan A dan B, tetapi tidak pada jenis lintasan yang menghubungkan titik A dan B, seperti yang ditunjukan pada gambar dibawah ini: B C 1 D C 2 A C 3 Nilai integeral pada lintasan c 1, c 2 dan c 3 adalah sama.

Teorema Jika A=ΔΦ Pada semua titik dalam suatu daerah J dari ruang, yang didefinisikan oleh : a 1 , ≤, x ≤ a 2 b 1 ≤ y ≤ b 2 , c 1 ≤ z ≤ c 2 , dimana Φ (x, y, z) berharga tunggal dan memiliki turunan yang kontinu dalam R, maka: 1. = tidak tergantung pada lintasan C dalam R yang menghubungkan p 1 dan p 2 2. mengelilingi setiap kurva tertutup C dalam R. Dalam hal demikian A disebut sebuah medan vektor konservatif dan Φ adalah potensial skalarnya. jadi sebuah medan vektor A adalah konservatif jika dan hanya jika x. A=0, atau juga ekivalen dengan A= Φ.

Contoh: 1. Diketahui F=( 2 xy+z 3 ) i + x 2 j+3 x z 2 k a. tunjukan bahwa F sebuah medan gaya konservatif b. carilah potensial skalar c. carilah usaha yang dilakukan dalam menggerakan sebuah benda dalam. Medan ini dari (1, -2, 1) ke (3, 1, 4). Jawab: a. Syarat perlu dan cukup agar sebuah daya konservatif adalah Curl F= xf=0

b. integrasikan (1), (2), dan (3), diperoleh masing-masing Dengan memilih F(y, z)=0, G(x, z)=xz 3 dan H(x, y) =x 2 y, maka diperoleh: Φ=x 2 y +x z 3 dengan tambahan sembarang konstanta.

c.

Contoh: Jika A = ( 4 x y – 3 k 2 z 2 ) i + 2 x 2 j – 2 x 3 z k Buktikan bahwa tidak tergantung lintasan c yang menghubungkan dua titik. Jawab : Jika tidak tergantung lintasan , maka A adalah medan konservatif. Kalau A medan konservatif , maka akan berlaku x A = 0. x. A = = i ( 0 ) – j ( - 6 x 2 z + 6 x 2 z ) + k ( 4 x – 4 x ) = 0

TEOREMA GREEN DALAM BIDANG 1. Teorema Green Dalam Bidang Jika R adalah suatu daerah tertutup dalam bidang xy yang dibatasi oleh kurva tertutup C dan jika M dan N adalaj fungsi-fungsi kontinu dari x dan y yang memiliki turunan-turunan kontinu dalam R, maka dimana C dilintasi dalam arah positif (berlawanan arah putaran jarum jam). Bila tidak ada pernyataan lain, kita akan selalu menganggap berarti bahwa integeralnya dimaksud dalam arah positif.

Contoh : Hitunglah (xy + y 2)dx + x 2 dy, dimana C adalah kurva tertutup dari daerah yang dibatasi oleh y = x dan y = x 2 dengan menggunakan teorema Green dalam bidang. Jawab: = =