INTEGRAL CALCULUS Integration Technical Mathematics Grade 12 Just

INTEGRAL CALCULUS (Integration) Technical Mathematics Grade 12 -Just In Time Training 17 February 2018 , Ishaak Cassim DCES: Technical Mathematics Ishaak Cassim - February 2018 1

Outcomes for this section • Ishaak Cassim - February 2018 2

Introduction Ishaak Cassim - February 2018 3

Activity 1 • Activity 1 • Write down at least five other functions whose derivative is 4 x. Ishaak Cassim - February 2018 4

Introduction • You would have noticed that all the functions have the same derivative of 4 x, because when we differentiate the constant term we obtain zero. • Hence, when we reverse the process, we have no idea what the original constant term might have been. • So we include in our response an unknown constant, c, called the arbitrary constant of integration. • The integral of 4 x then is 2 x 2 + c. Ishaak Cassim - February 2018 5

Introduction • Ishaak Cassim - February 2018 6

Introduction Ishaak Cassim - February 2018 7

• Ishaak Cassim - February 2018 8

Definition of anti-derivative • Ishaak Cassim - February 2018 9

Activity 2 Ishaak Cassim - February 2018 10

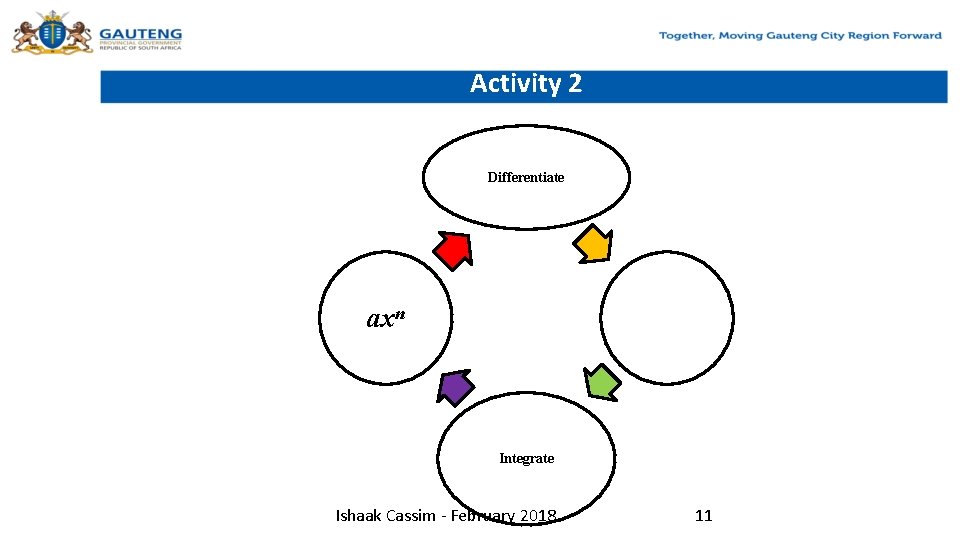
Activity 2 Differentiate axn Integrate Ishaak Cassim - February 2018 11

The general solution of integrals of the form kxn • Ishaak Cassim - February 2018 12

Table of ready to use integrals Function, f (x)= k , where k is a constant f (x)= x f (x) = x 2 f(x) = axn f (x) = kanx Ishaak Cassim - February 2018 13

Worked Examples: Indefinite integrals a) Ishaak Cassim - February 2018 14

Worked Examples: Indefinite integrals c) Note: in this example, we are integrating with respect to u. Explain the method used Ishaak Cassim - February 2018 15

Worked Examples: Indefinite integrals d) Complete Ishaak Cassim - February 2018 16

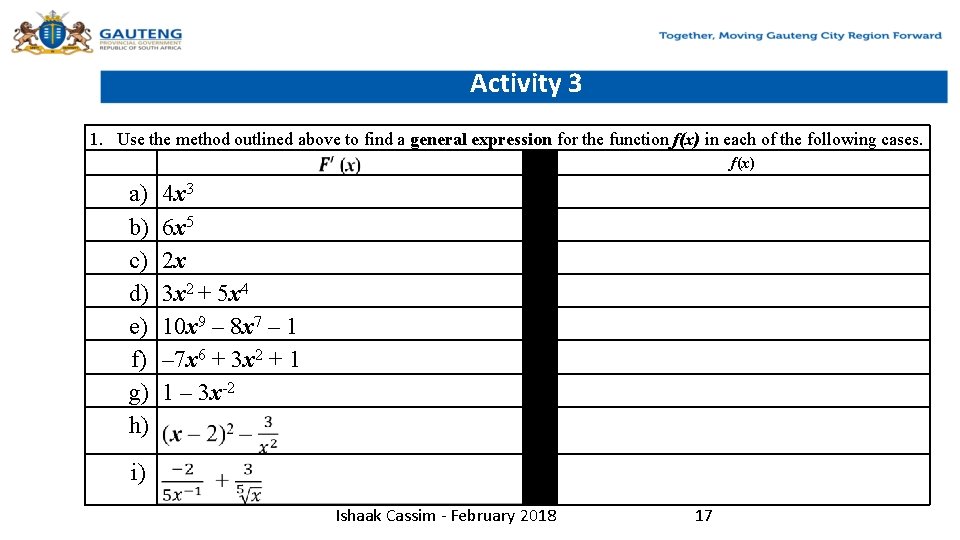
Activity 3 1. Use the method outlined above to find a general expression for the function f(x) in each of the following cases. f(x) a) 4 x 3 b) c) d) e) f) g) h) i) 6 x 5 2 x 3 x 2 + 5 x 4 10 x 9 – 8 x 7 – 1 – 7 x 6 + 3 x 2 + 1 1 – 3 x-2 Ishaak Cassim - February 2018 17

Activty 3 - continued 2. Determine the indefinite integrals in the following cases a) b) c) d) e) f) g) h) 3. Determine the following indefinite integrals a) b) c) d) e) f) Ishaak Cassim - February 2018 18

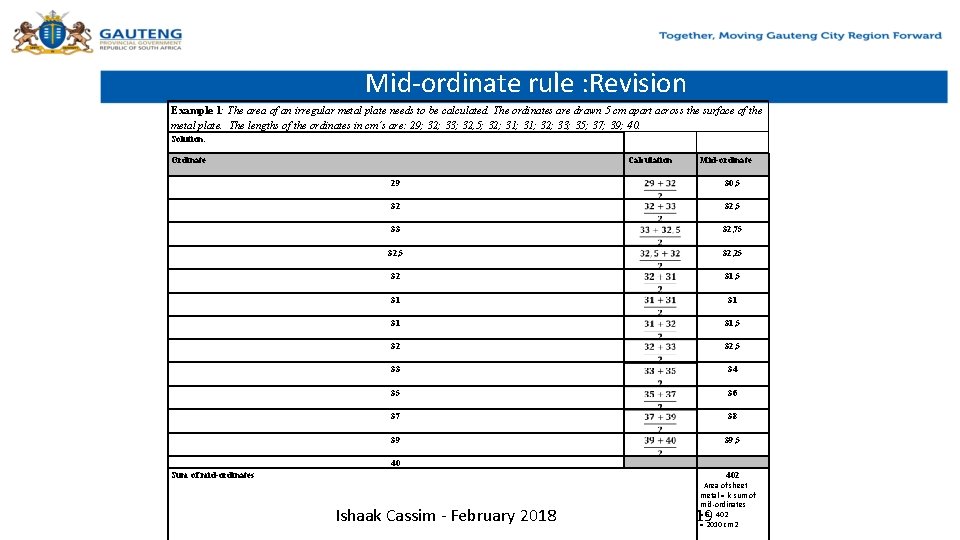
Mid-ordinate rule : Revision Example 1: The area of an irregular metal plate needs to be calculated. The ordinates are drawn 5 cm apart across the surface of the metal plate. The lengths of the ordinates in cm’s are: 29; 32; 33; 32, 5; 32; 31; 32; 33; 35; 37; 39; 40. Solution: Ordinate Calculation Mid-ordinate 29 30, 5 32 32, 5 33 32, 75 32, 25 32 31, 5 31 31, 5 32 32, 5 33 34 35 36 37 38 39 39, 5 40 402 Sum of mid-ordinates Ishaak Cassim - February 2018 Area of sheet metal = k sum of mid-ordinates = 5 402 = 2010 cm 2 19

Area of irregular shapes- Revision • Ishaak Cassim - February 2018 20

Revision: Area of irregular shapes • Ishaak Cassim - February 2018 21

Example 2: Area of irregular shape Example 2: Determine the area of an irregular metal plate. Ordinates are drawn 1, 5 cm apart. The lengths of the ordinates in cm are: 0; 30; 42; 49; 56; 46; 38; 30; 18; 0 Ishaak Cassim - February 2018 22

B F C A Ishaak Cassim - February 2018 E 23 D

Introduction to definite integral In the figure above, OABC is bounded by a base OC , two vertical ordinates OA and BC and a curve AB. Ishaak Cassim - February 2018 24

Introduction to definite intrgral • Ishaak Cassim - February 2018 25

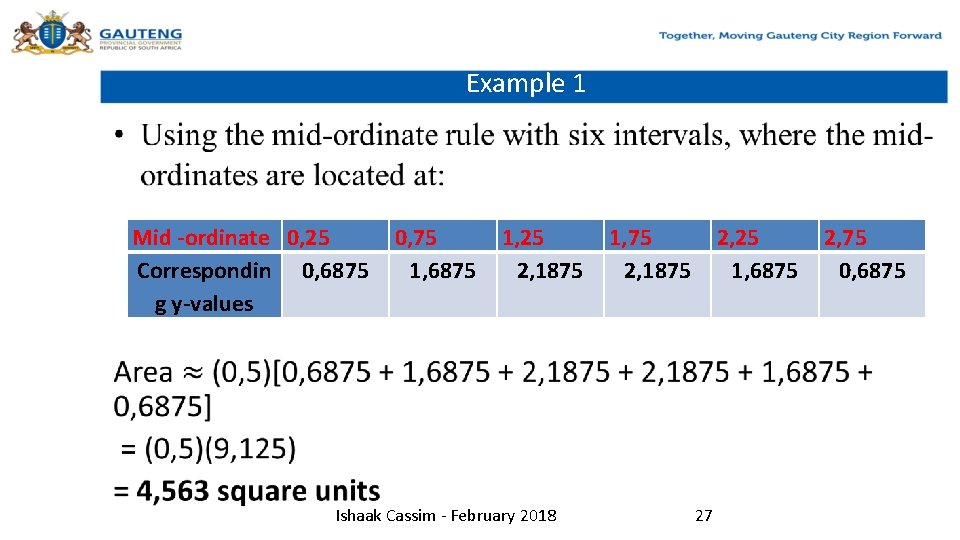
Example 1 • Consider the following example: Plot the graph of y = 3 x –x 2, by completing a table of values of y from x = 0 to x = 3. • Determine the area enclosed by the curve, the x-axis and ordinates x = 0 and x = 3 using the mid-ordinate rule. x 0 0, 5 1, 0 1, 5 2, 0 2, 5 3, 0 y = 3 x – x 2 0 1, 25 2 2, 25 2 1, 25 0 Ishaak Cassim - February 2018 26

Example 1 • Mid -ordinate 0, 25 Correspondin 0, 6875 g y-values 0, 75 1, 6875 1, 25 2, 1875 Ishaak Cassim - February 2018 1, 75 2, 1875 2, 25 1, 6875 27 2, 75 0, 6875

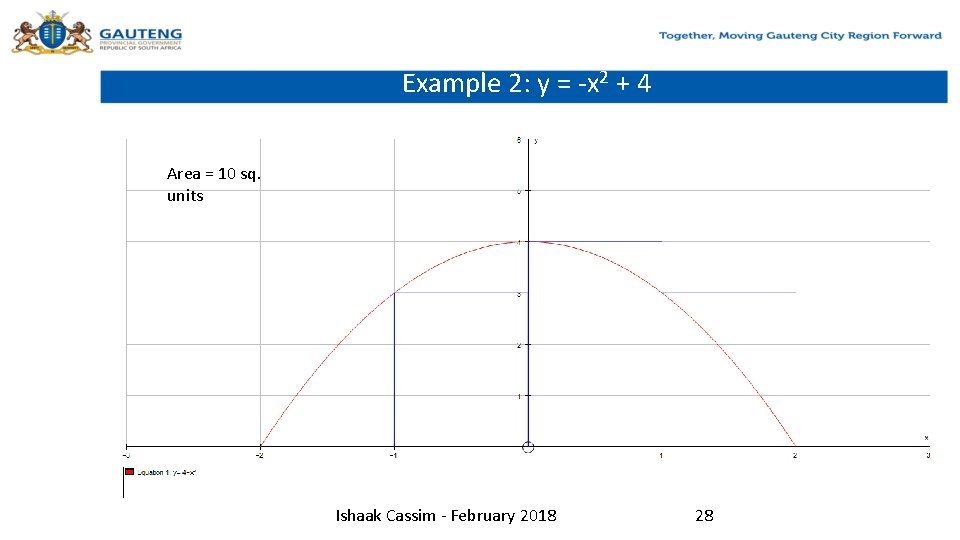
Example 2: y = -x 2 + 4 Area = 10 sq. units Ishaak Cassim - February 2018 28

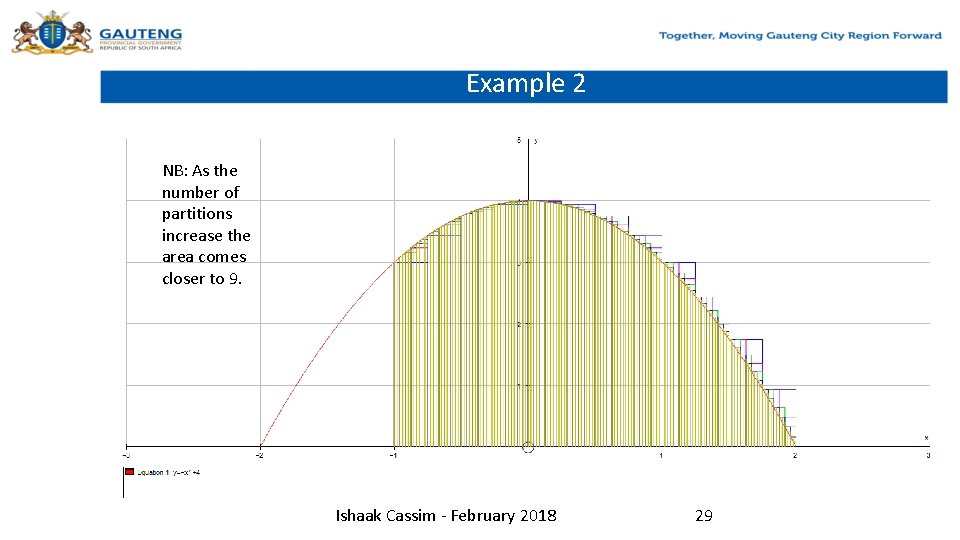
Example 2 NB: As the number of partitions increase the area comes closer to 9. Ishaak Cassim - February 2018 29

Activity 4 1. a) b) c) d) e) Using rectangles, calculate the areas described in each of the following cases. Use a partition with a sensible number of rectangles. Make sure each rectangle has the same width. Make a rough sketch for each case. f(x) = 2 x + 7 between the x-axis, and x = – 2 and x = 3. k(x) = x 2 bounded by the x –axis and x = – 4 and x = – 1. m(x) = x 2 + 2, between the x-axis and x = – 5 and x = 3. Is this area an under- or overestimate of the true area? f) 2. Create an Excel spreadsheet to approximate the area bounded by the curve t(x) = –x 2 + 4 on the interval [– 1 ; 2] for 3 different rectangle widths. 3. 1 How does this method compare with method of dividing the given interval into rectangles? Ishaak Cassim - February 2018 30

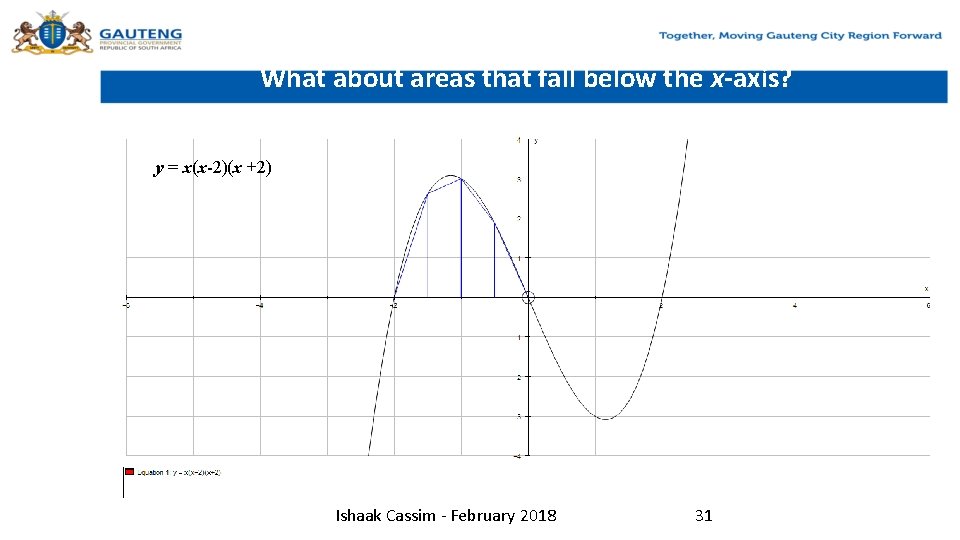
What about areas that fall below the x-axis? y = x(x-2)(x +2) Ishaak Cassim - February 2018 31

Area below the x-axis • Ishaak Cassim - February 2018 32

The definite integral • Ishaak Cassim - February 2018 33

The definite integral • Ishaak Cassim - February 2018 34

The fundamental Theorem of Calculus • Ishaak Cassim - February 2018 35

Worked examples – the definite integral Evaluate the following definite integrals 1 Ishaak Cassim - February 2018 36

Worked examples – the definite integral Evaluate the following definite integrals 2. Ishaak Cassim - February 2018 37

Worked examples- The definite integral 3. Ishaak Cassim - February 2018 38

Worked examples- The definite integral 4. Ishaak Cassim - February 2018 39

Activity 5 1. Evaluate the following definite integrals, using the method outlined above. a) b) c) d) e) f) g) h) Ishaak Cassim - February 2018 40

Some properties of integrals Here are some simple properties of the integral that are often used in computations. Throughout take f and g as continuous functions. 1. 2. 3 4. 5. Ishaak Cassim - February 2018 41

Activity 6 • Ishaak Cassim - February 2018 42

Activity 7 • Ishaak Cassim - February 2018 43

Activity 8 1. 2. 3. 4. Ishaak Cassim - February 2018 44

Area under a curve • Use the properties of definite integrals developed in the previous section to calculate the area under a curve. • NB: If asked to evaluate a definite integral without explicitly asked to calculate the area, then proceed to evaluate the definite integral without concern about the answer-i. e the answer can be 0 or a negative value!! Ishaak Cassim - February 2018 45

Area under a curve- Worked example • Find the area under the curve y = x 2 , between x = 1 and x = 3. Ishaak Cassim - February 2018 46

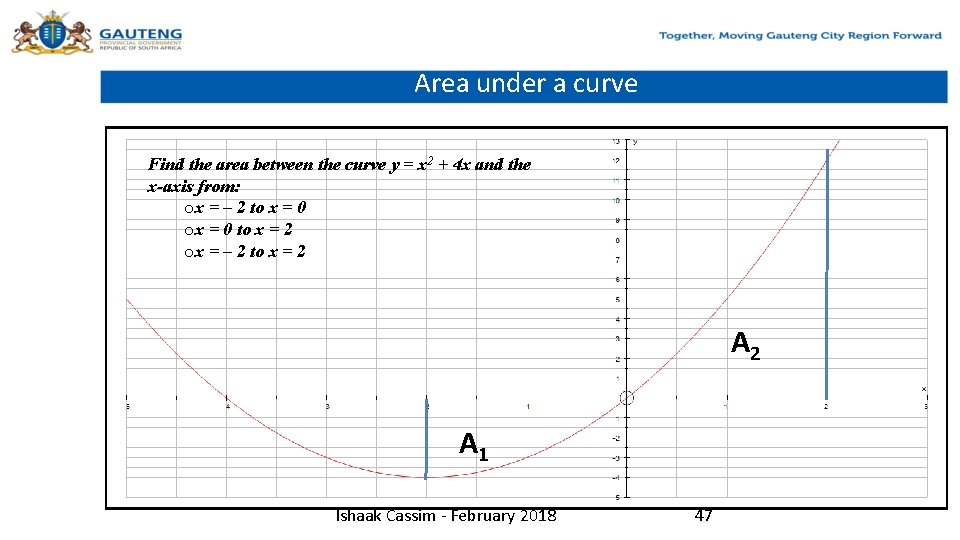
Area under a curve Find the area between the curve y = x 2 + 4 x and the x-axis from: ox = – 2 to x = 0 ox = 0 to x = 2 ox = – 2 to x = 2 A 1 Ishaak Cassim - February 2018 47

Worked example 2 • Ishaak Cassim - February 2018 48

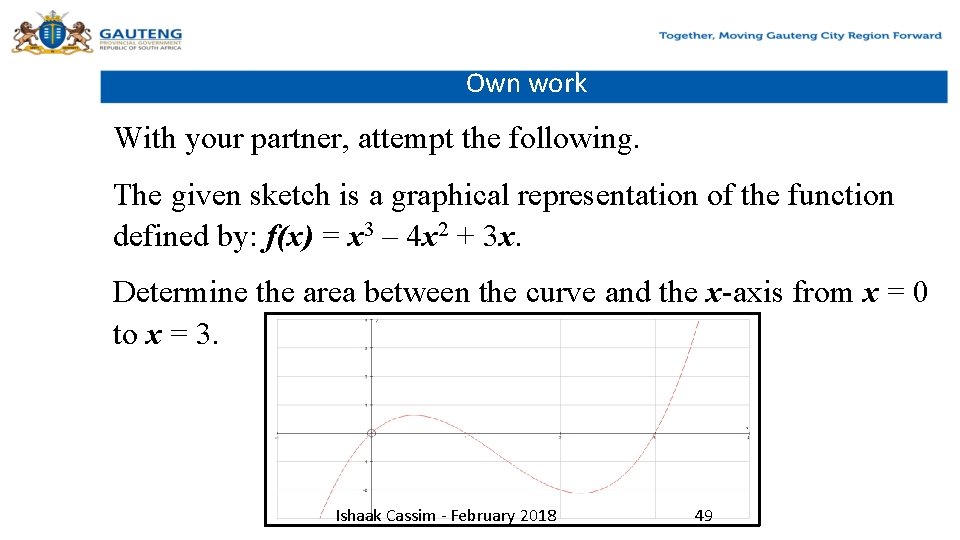
Own work With your partner, attempt the following. The given sketch is a graphical representation of the function defined by: f(x) = x 3 – 4 x 2 + 3 x. Determine the area between the curve and the x-axis from x = 0 to x = 3. Ishaak Cassim - February 2018 49

Challenge • Find the area enclosed between the curve 2 y = x – 2 x – 3 and the straight-line y = x + 1. Ishaak Cassim - February 2018 50

Activity 9 1. a) c) 2. a) c) Use the properties of definite integrals which you have studied thus far, to evaluate the following definite integrals. b) d) Calculate the areas of the following: b) d) Ishaak Cassim - February 2018 51

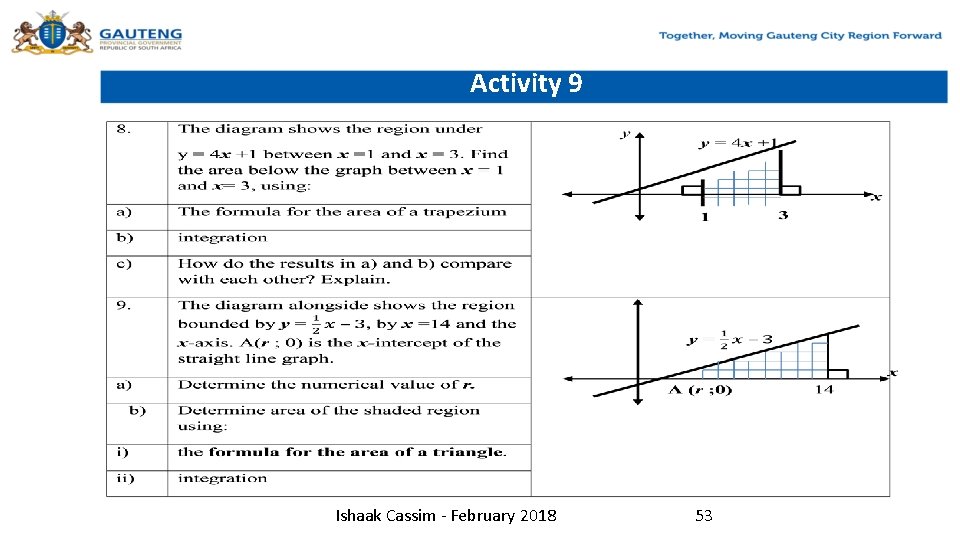
Activity 9 3. 4. 5. 6. a) c) 7. a) b) c) Find the area under the curve y = x 2 from x = 0 to x = 6. Find the area under the curve y = 3 x 2 + 2 x from x = 0 to x = 4. Find the area under the curve y = 3 x 2 -2 x from x = – 4 to x = 0. Find the area enclosed by the x-axis and the following curves and straight lines. y = x 2 + 3 x ; x = 2 ; x =5 b) y = (3 x– 4)2 ; x = 1 , x =3 d) y = 2 – x 3 ; x = – 3 ; x = – 2 Sketch the curve y = x(x +1)(x – 3), showing where it cuts the x-axis. Calculate area of the region, above the x-axis, bounded by the x-axis and the curve. Calculate area of the region, below the x-axis, bounded by the x-axis and the Ishaak Cassim - February 2018 52 curve.

Activity 9 Ishaak Cassim - February 2018 53

Activity 9 10. Calculate the areas of the following: a) y = 1 + x 2 for b) 0 < x < 2 11. 12. 13. 14. Ishaak Cassim - February 2018 54

Conclusion Ishaak Cassim - February 2018 55