Integrable and NonIntegrable Rigid Body Dynamics Actions and

Integrable and Non-Integrable Rigid Body Dynamics – Actions and Poincare Sections Classical Problems of Rigid Body Dynamics International Conference Dedicated to the 300 th anniversary of Leonhard Euler Donetsk 9 -13 June 2007 Peter Richter Institute for Theoretical Physics 1

Parameter space of standard rigid bodies No translation 3 rotational degrees of freedom of SO(3) type 4 parameters principal moments of inertia 2: A 1, a. A 2=, A 32/A 1, b = A 3/A 1 center of gravity s 2: 1, r, s 2, ss 3 Remark: a Cardan suspension implies T 3 rather than SO(3) as configurations space; it requires at least two more parameters for the moment of inertia of the suspension device, and the direction of its axis relative to gravity. Peter Richter Institute for Theoretical Physics 2

Integrable and non-integrable rigid body dynamics • Phase spaces and basic equations - Full and reduced phase spaces - Equations of motion • Integrable cases: Actions - Euler - Lagrange - Kovalevskaya • Non-integrable dynamics: Poincaré sections - General principles - The PP-torus representation - An example Peter Richter Institute for Theoretical Physics 3

Phase space and conserved quantities 3 angles + 3 velocities 6 D phase space 4 conserved quantities: energy h, angular momenta lx, ly, lz → 2 D invariant sets, super-integrable dynamics 3 conserved quantities: energy h, momenta lz, l 3 → 3 D invariant sets, integrable dynamics 3 conserved quantities: energy h, momentum lz, and K → 3 D invariant sets, integrable In general: only 2 conserved quantities: energy h and momentum lz → 4 D invariant sets, (mildly) chaotic dynamics Peter Richter Institute for Theoretical Physics 4

Reduced phase space The 6 D phase space of variables g=(g 1, g 2, g 3) and l = (l 1, l 2, l 3) has Casimir constants g 2=1 (Poisson sphere) and l·g = lz, hence is effectively 4 D 3 conserved quantities: energy h, angular momenta lx, ly → 1 D invariant sets, super-integrable dynamics 2 conserved quantities: energy h, momentum l 3 → 2 D invariant sets, integrable dynamics 2 conserved quantities: energy h, Kovalevskaya K → 2 D invariant sets, integrable In general: only 1 conserved quantity: energy h → 3 D invariant sets, (mildly) chaotic dynamics Peter Richter Institute for Theoretical Physics 5

Euler-Poisson equations coordinates phase space with Poisson structure and 2 Casimirs Hamiltonian equations of motion general constant: energy effective potential Peter Richter Institute for Theoretical Physics 6

Canonical equations with Euler angles phase space coordinates Hamiltonians: Euler‘s case Lagrange‘s case Peter Richter Institute for Theoretical Physics 7

Integrable and non-integrable rigid body dynamics • Phase spaces and basic equations - Full and reduced phase spaces - Equations of motion • Integrable cases: Actions - Euler - Lagrange - Kovalevskaya • Non-integrable dynamics: Poincaré sections - General principles - The PP-torus representation - An example Peter Richter Institute for Theoretical Physics 8

Actions in the Euler case actions j-action: J, y-actions: complete elliptic integrals of the third kind Energy surfaces h = h(I 1, I 2, I 3) carry information on frequencies, winding numbers, bifurcations (separatrices), and quantum mechanics. Peter Richter Institute for Theoretical Physics 9

Actions in the Euler case Energy surfaces in action representation: 1: 1 correspondence of points and Liouville tori Q 1 = Q 2 = Q 3 Q 1 = 1. 5, Q 2 = 2, Q 3 = 1 Ij towards left front, Iy towards right, IJ pointing up only one quarter is shown: Ij and Iy may be positive and negative, depending on sense of rotation Peter Richter Institute for Theoretical Physics 10

Actions in the Lagrange case actions j-action: y-action: J-action: complete elliptic integral of the third kind Frequencies are integrals of the first kind, winding numbers are of the third kind Peter Richter Institute for Theoretical Physics 11

Actions in the Lagrange case Q 3 = 2 Q 1 = 2 Q 2 E=0 Q 3 = Q 1 = Q 2 E=1 2 Q 3 = Q 1 = Q 2 E = 1. 5 E=4 Q 3 = 0. 6 Q 1 Ij towards right, Iy towards back, IJ pointing up only one half is shown: surfaces are symmetric with respect to Ij, Iy → -Ij , -Iy Peter Richter Institute for Theoretical Physics 12

Actions in the Kovalevskaya case j-action: I 1 = lj = l ds s 1, s 2 -actions: hyperelliptic integral with paths to be determined on a hyperelliptic curve Kovalevskaya‘s polynomials: s-coordinate w. r. t. pole h w. r. t. Appelrot-transition Peter Richter Institute for Theoretical Physics 13

Actions in the Kovalevskaya case Energy surfaces in action representation: agreement of numerical computation with Abelian integrals h = -0. 5 h = 0. 9 h = 1. 2 h = 1. 45 h = 2. 3 h = 9. 0 Ij towards right front, I 2 towards left front, I 3 pointing up Peter Richter Institute for Theoretical Physics 14

Integrable and non-integrable rigid body dynamics • Phase spaces and basic equations - Full and reduced phase spaces - Equations of motion • Integrable cases: Actions - Euler - Lagrange - Kovalevskaya • Non-integrable dynamics: Poincaré sections - General principles - The PP-torus representation - An example Peter Richter Institute for Theoretical Physics 15

Poincaré surfaces of section: general considerations Find a surface P 2 h, l in E 3 h, l such that every trajectory meets it repeatedly. Recipe: choose bounded W: E 3 h, l → R and take S : = d. W/dt = 0 as section condition. Then look for a convenient surface to which P 2 h, l can be mapped 1: 1. S+(g) S─(g) P 2 h, l Finally, identify points on S+( g) and S─(g) whose preimages are identical. Peter Richter Institute for Theoretical Physics 16

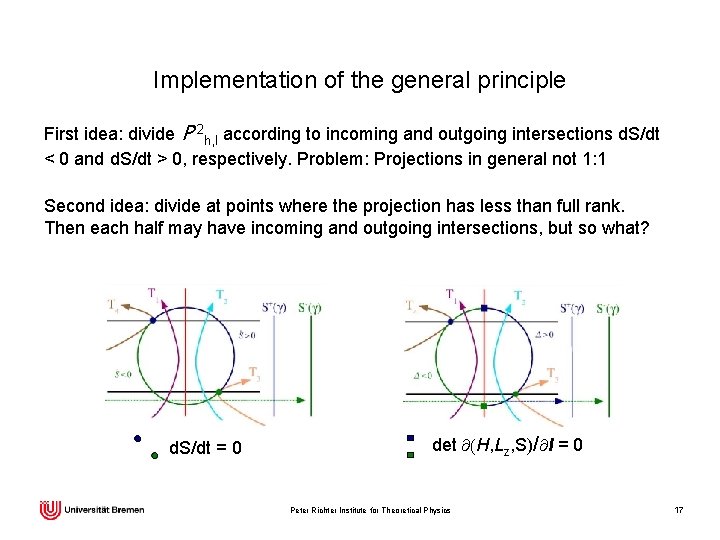
Implementation of the general principle First idea: divide P 2 h, l according to incoming and outgoing intersections d. S/dt < 0 and d. S/dt > 0, respectively. Problem: Projections in general not 1: 1 Second idea: divide at points where the projection has less than full rank. Then each half may have incoming and outgoing intersections, but so what? d. S/dt = 0 det (H, Lz, S)/ l = 0 Peter Richter Institute for Theoretical Physics 17

The situation in rigid body dynamics Let the section condition be defined by W = g ∙ s, hence S = A-1 l ∙ (s x g) = 0. The surface P 2 h, l so defined projects to the Poisson sphere as follows: Its image is the entire accessible region Uh, l = { Ul(g) ≤ h } in S 2(g). Points on the boundary Uh, l have one preimage. The preimage of the two points g = ± s /s is a circle. All other points of Uh, l have exactly two preimages. This suggests the construction of the PP-torus (from Poisson and Poincaré). Peter Richter Institute for Theoretical Physics 18

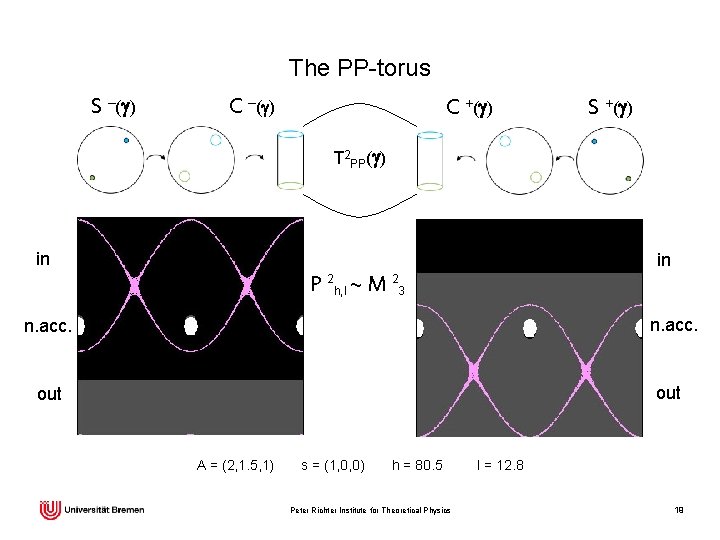
The PP-torus S ─ (g ) C ─(g) C + (g ) S + (g ) T 2 PP(g) in in P 2 h, l ~ M 23 n. acc. out A = (2, 1. 5, 1) s = (1, 0, 0) h = 80. 5 Peter Richter Institute for Theoretical Physics l = 12. 8 19

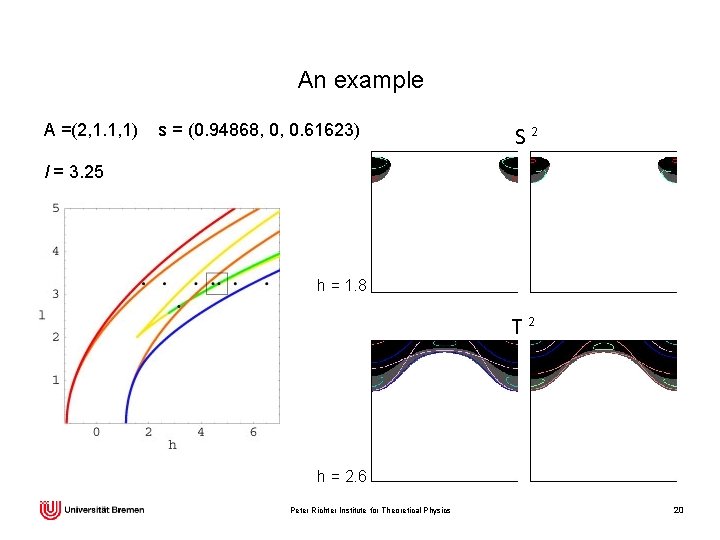
An example A =(2, 1. 1, 1) s = (0. 94868, 0, 0. 61623) S 2 l = 3. 25 h = 1. 8 T 2 h = 2. 6 Peter Richter Institute for Theoretical Physics 20

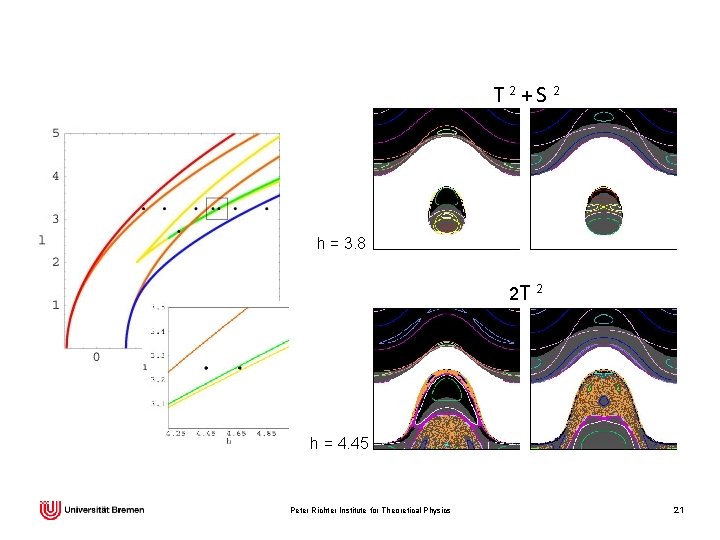
T 2+S 2 h = 3. 8 2 T 2 h = 4. 45 Peter Richter Institute for Theoretical Physics 21

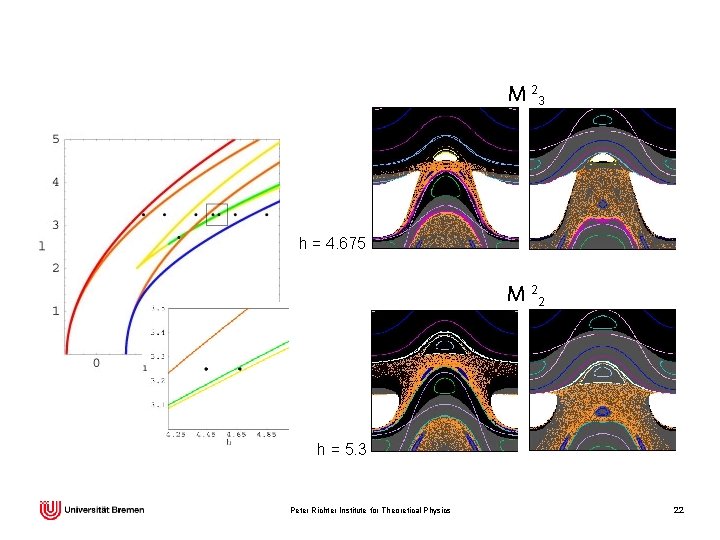
M 23 h = 4. 675 M 22 h = 5. 3 Peter Richter Institute for Theoretical Physics 22

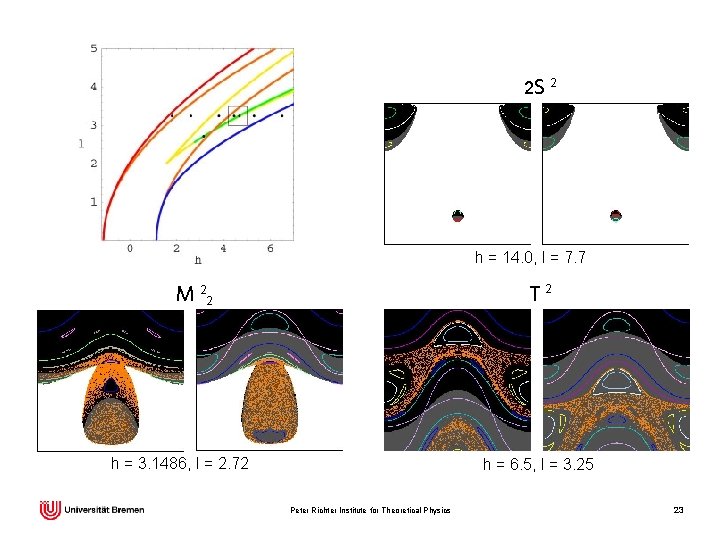
2 S 2 h = 14. 0, l = 7. 7 T 2 M 22 h = 3. 1486, l = 2. 72 h = 6. 5, l = 3. 25 Peter Richter Institute for Theoretical Physics 23

Integrable and non-integrable rigid body dynamics - Phase spaces and basic equations • Full and reduced phase spaces • Equations of motion - Integrable cases: Actions • Euler • Lagrange • Kovalevskaya - Non-integrable dynamics: Poincaré sections - General principles • The PP-torus representation • An example Peter Richter Institute for Theoretical Physics 24

Outlook • Semiclassical quantization of the integrable cases via actions • Collect knowledge about non-integrable dynamics; very little seems to be known • Consider rigid bodies with Cardan suspension: the configuration space is then not SO(3) but T 3 Peter Richter Institute for Theoretical Physics 25

Acknowlegdements • • Mikhail Kharlamov Igor Gashenenko Alexey Bolsinov Alexander Veselov Holger Dullin Andreas Wittek Dennis Lorek Sven Schmidt Peter Richter Institute for Theoretical Physics 26

Peter Richter Institute for Theoretical Physics 27

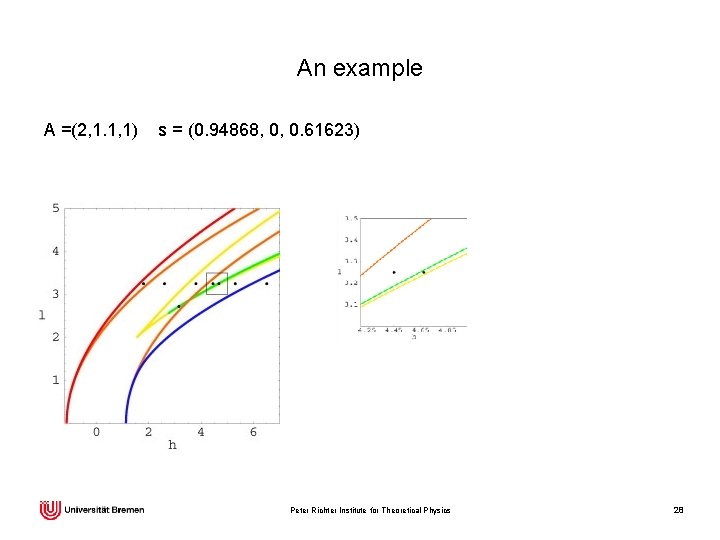
An example A =(2, 1. 1, 1) s = (0. 94868, 0, 0. 61623) Peter Richter Institute for Theoretical Physics 28

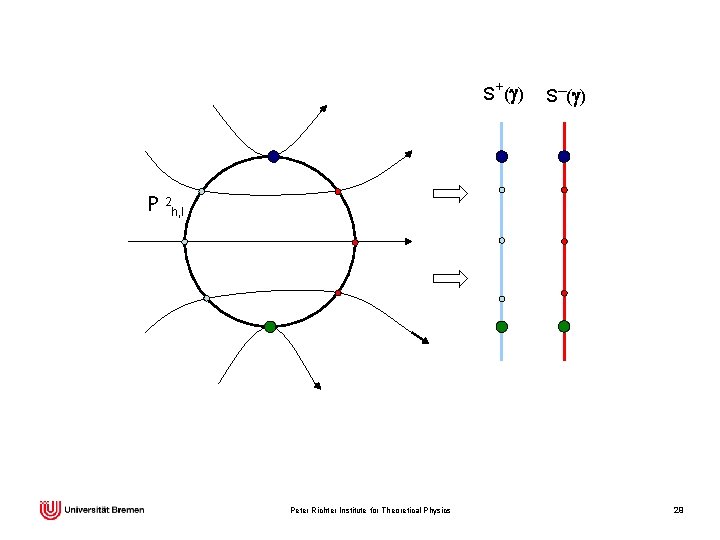
S + (g ) S─(g) P 2 h, l Peter Richter Institute for Theoretical Physics 29