Integer Sorting on the wordRAM Uri Zwick Tel

Integer Sorting on the word-RAM Uri Zwick Tel Aviv University Started: May 2015 Last update: December 21, 2016 1

Integer sorting 2

Comparison based algorithms Some of these algorithms are randomized and some use multiplications 3

Fundamental open problem 4

Variants of Sorting Each item in the array to be sorted: info First choice: (Stably) sort the array or return a permutation that (stably) sorts the array. key Second choice: info bits important or info bits may be destroyed. 5

Variants of Sorting Use radix-sort or “double-precision”. Using hashing. 6

(Adapted from Cormen, Leiserson, Rivest and Stein, Introduction to Algorithms, Third Edition, 2009, p. 195) 7

Backward/LSD Radix sort Stably sort according to “digits”. Starting from least significant digit. 2 8 7 1 4 5 9 1 6 5 7 2 1 3 0 1 6 5 7 2 2 4 7 2 3 5 5 5 7 0 2 2 8 3 9 4 4 8 4 4 3 5 5 5 3 6 3 5 3 6 To sort according to a “digit” use bucket or count sort. Slides from undergrad course 8

Backward/LSD Radix sort Stably sort according to “digits”. Starting from least significant digit. 2 8 7 1 4 5 9 1 1 3 0 1 6 5 7 2 2 4 7 2 7 0 2 2 8 3 9 4 4 8 4 4 3 5 5 5 3 6 9

Backward/LSD Radix sort Stably sort according to “digits”. Starting from least significant digit. 2 8 7 1 1 3 0 1 4 5 9 1 7 0 2 2 1 3 0 1 3 5 3 6 6 5 7 2 4 8 4 4 2 4 7 2 3 5 5 5 7 0 2 2 2 8 7 1 8 3 9 4 6 5 7 2 4 8 4 4 2 4 7 2 3 5 5 5 4 5 9 1 3 5 3 6 8 3 9 4 10

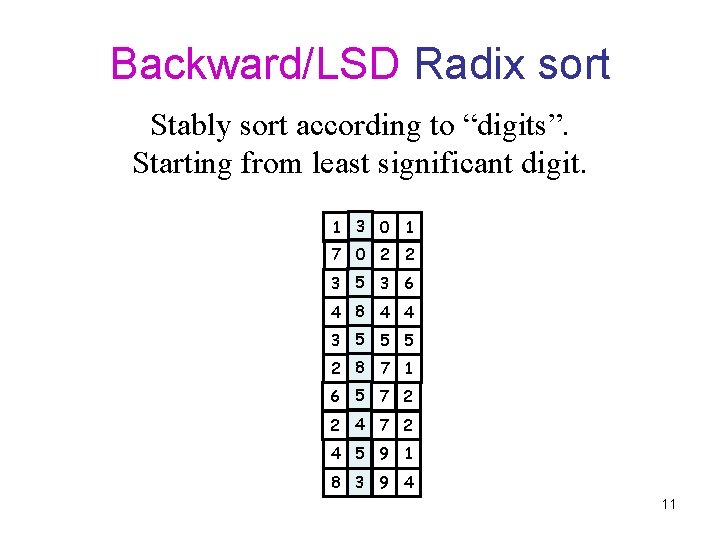
Backward/LSD Radix sort Stably sort according to “digits”. Starting from least significant digit. 1 3 0 1 7 0 2 2 3 5 3 6 4 8 4 4 3 5 5 5 2 8 7 1 6 5 7 2 2 4 7 2 4 5 9 1 8 3 9 4 11

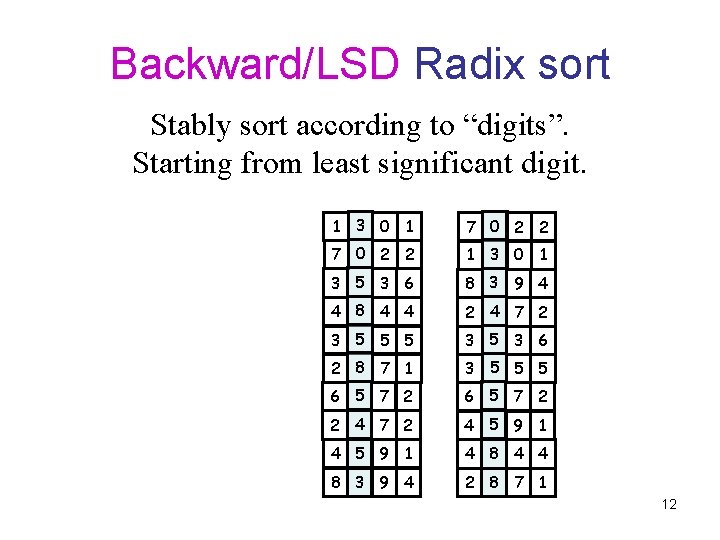
Backward/LSD Radix sort Stably sort according to “digits”. Starting from least significant digit. 1 3 0 1 7 0 2 2 1 3 0 1 3 5 3 6 8 3 9 4 4 8 4 4 2 4 7 2 3 5 5 5 3 6 2 8 7 1 3 5 5 5 6 5 7 2 2 4 7 2 4 5 9 1 4 8 4 4 8 3 9 4 2 8 7 1 12

Backward/LSD Radix sort Stably sort according to “digits”. Starting from least significant digit. 7 0 2 2 1 3 0 1 8 3 9 4 2 4 7 2 3 5 3 6 3 5 5 5 6 5 7 2 4 5 9 1 4 8 4 4 2 8 7 1 13

Backward/LSD Radix sort Stably sort according to “digits”. Starting from least significant digit. 7 0 2 2 1 3 0 1 2 4 7 2 8 3 9 4 2 8 7 1 2 4 7 2 3 5 3 6 3 5 5 5 4 5 9 1 6 5 7 2 4 8 4 4 7 0 2 2 2 8 7 1 8 3 9 4 14

Backward/LSD Radix Sort in the word-RAM model Can we do better? 15

Two techniques Range reduction Packed sorting (Word-level parallelism) 16

Four results We will cover the following results: 17

Reminder: Bucket Sort Each item in the array to be sorted: info key Time and space for initializing and scanning the buckets 18

Bucket Sort using hashing Each item in the array : info key 19

Range reduction [Kirkpatrick-Reisch (1984)] info key high low Cleverly combine the two sorting steps into one. 20

Range reduction [Kirkpatrick-Reisch (1984)] 21

Range reduction [Kirkpatrick-Reisch (1984)] Sort the list of non-empty buckets. ? 22

Range reduction [Kirkpatrick-Reisch (1984)] Concatenate the lists in the non-empty buckets. 23

Range reduction [Kirkpatrick-Reisch (1984)] The algorithm sorts correctly. Same complexity may be obtained using van Emde Boas trees. 24

25

(Code fixed) 26

Packed representation 0 0 0 0 test bits 0 27

Packed representation Useful constants: 1 00… 0 1 0 0 0 1 1 0 0 Exercise: How quickly can these constants be computed? 28

Packed representation 1 00… 0 1 0 0 11… 1 0 0 00… 0 0 11… 1 1 29

Packed Sorting [Paul-Simon (1980)] [Albers-Hagerup (1997)] Sort each group naïvely. (For the time being. ) Pack each group into a single word. 30

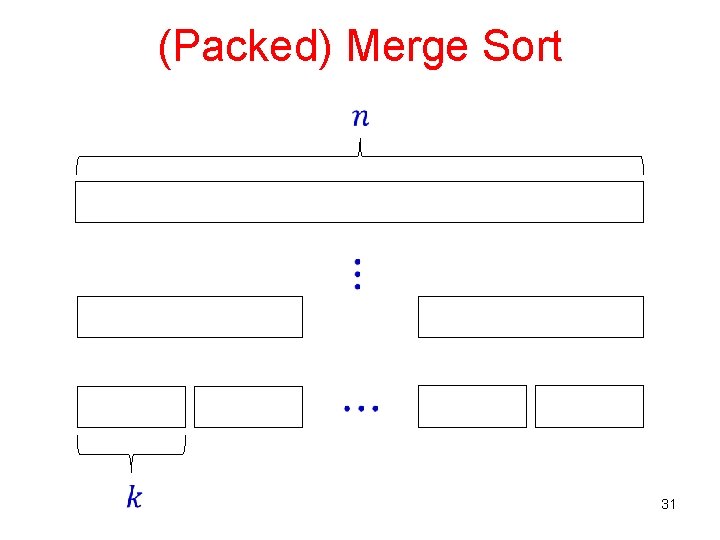
(Packed) Merge Sort 31

Packed Merge Sort [Paul-Simon (1980)] [Albers-Hagerup (1997)] 32

Packed Merge Sort [Paul-Simon (1980)] [Albers-Hagerup (1997)] 33

Packed Merge Sort [Paul-Simon (1980)] [Albers-Hagerup (1997)] 34

Packed Merge Sort [Paul-Simon (1980)] [Albers-Hagerup (1997)] 35

Packed Merge Sort [Paul-Simon (1980)] [Albers-Hagerup (1997)] 36

Packed Merge Sort [Paul-Simon (1980)] [Albers-Hagerup (1997)] 37

Packed Merge Sort [Paul-Simon (1980)] [Albers-Hagerup (1997)] 38

Packed Merge Sort [Paul-Simon (1980)] [Albers-Hagerup (1997)] Simple solution: Add a bit to each key, telling where it is coming form. Count number of keys coming from each sequence. (How do we count? ) 39

Batcher’s bitonic sort We need to reverse one of the sequences and concatenate it to the other sequence. 40

One step of bitonic sort (1) 0 0 0000 0 0000 0 0000 0 0 41

One step of bitonic sort (2) 0 0 0 0000 0 0000 0 0 42

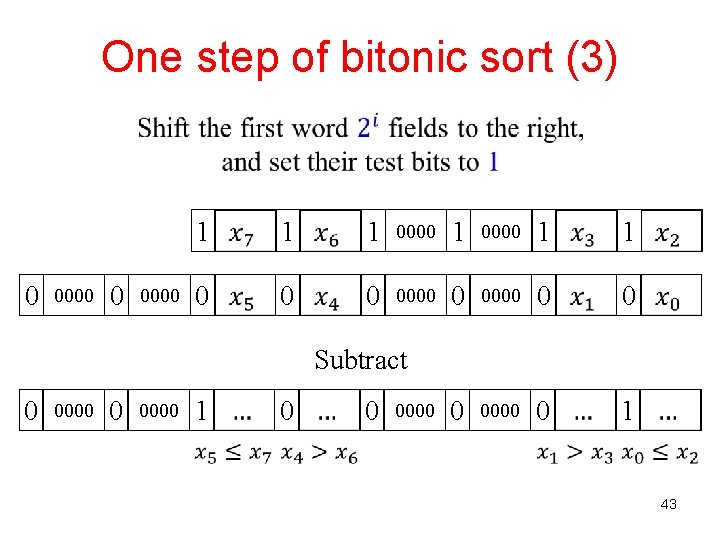
One step of bitonic sort (3) 0 0000 1 1 1 0000 1 1 0 0000 0 0 0 0000 0 1 Subtract 0 0000 1 0 0 0000 43

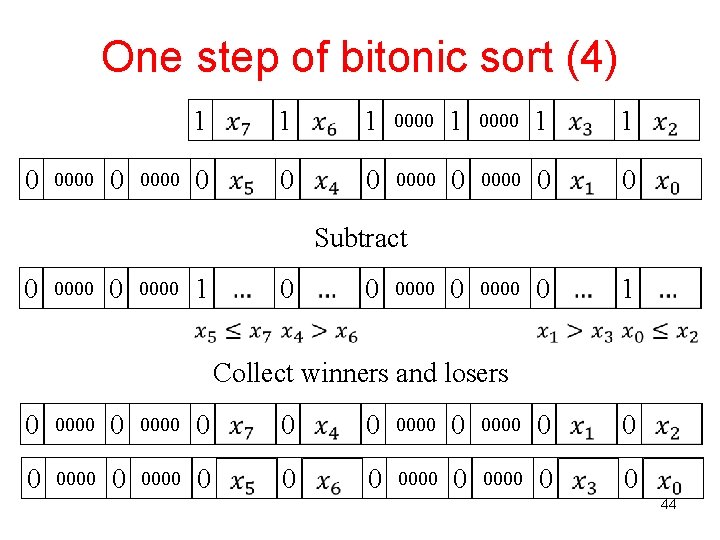
One step of bitonic sort (4) 0 0000 1 1 1 0000 1 1 0 0000 0 0 0 0000 0 1 Subtract 0 0000 1 0 0 0000 Collect winners and losers 0 0000 0 0000 0 0 44

One step of bitonic sort (5) 0 0000 0 0000 0 0 45

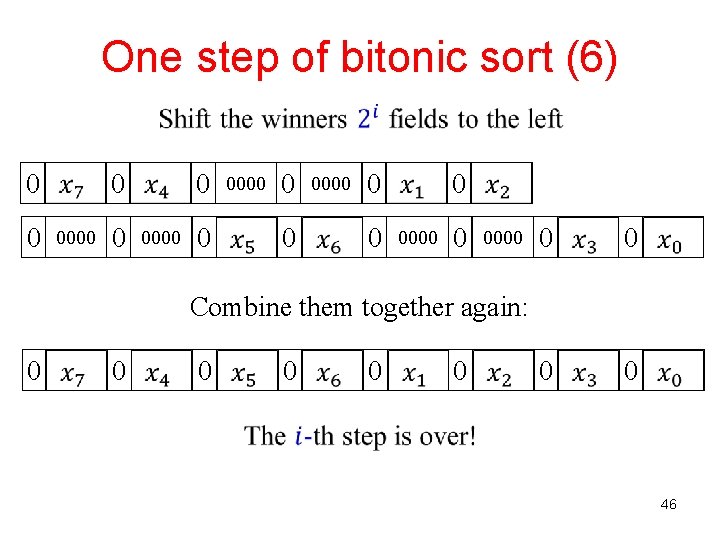
One step of bitonic sort (6) 0 0 0 0000 0 0000 0 0 0 0 Combine them together again: 0 0 0 46

Packed Bitonic Sort [Albers-Hagerup (1997)] 47

Packed Bitonic Sort [Albers-Hagerup (1997)] 48

Reversing the fields in a word Similar to the implementation of bitonic sort. We already know how to do it. Exercise: Show that this indeed reverses the fields. 49

Packed Merge Sort 50

How much space are we using? Are we using multiplications? Yes! In the hashing. 51

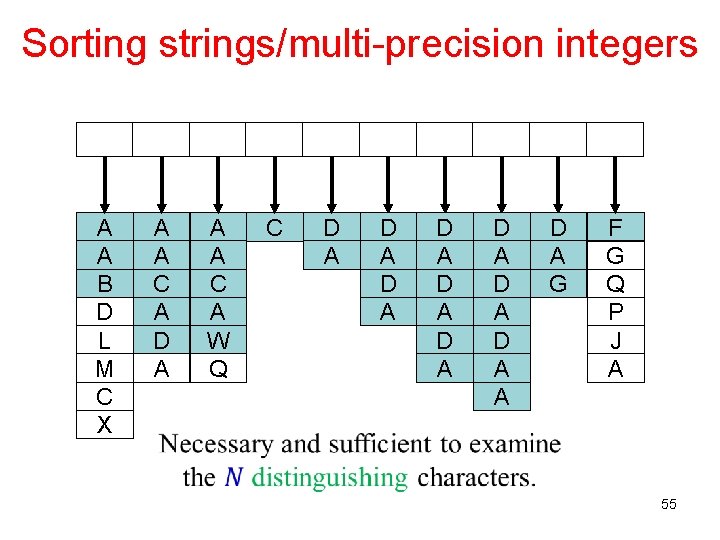
Sorting strings/multi-precision integers We want to sort them lexicographically. 52

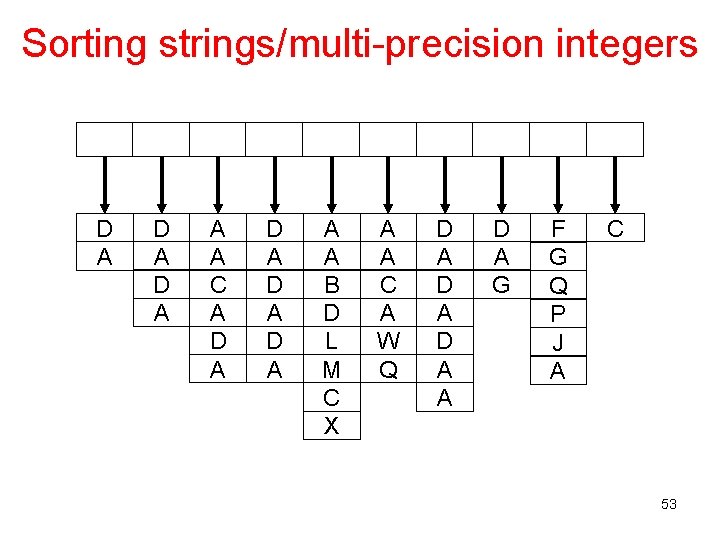
Sorting strings/multi-precision integers D A D A A A C A D A D A A A B D L M C X A A C A W Q D A D A G F G Q P J A C 53

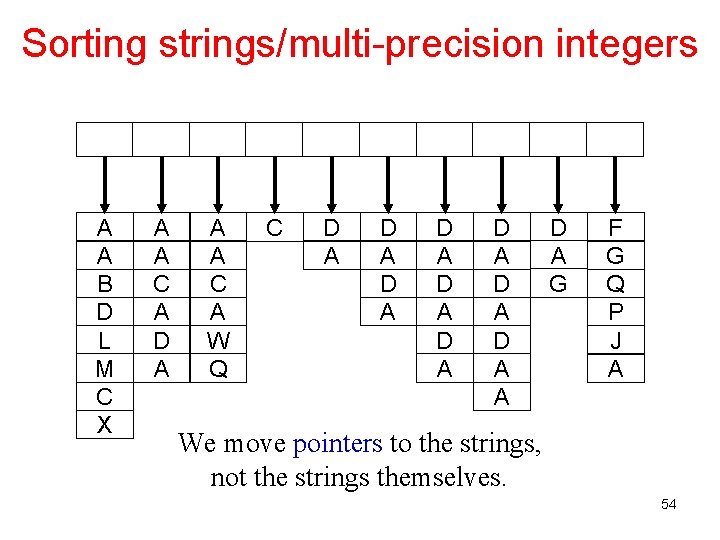
Sorting strings/multi-precision integers A A B D L M C X A A C A D A A A C A W Q C D A D A D A A D A G F G Q P J A We move pointers to the strings, not the strings themselves. 54

Sorting strings/multi-precision integers A A B D L M C X A A C A D A A A C A W Q C D A D A D A A D A G F G Q P J A 55

Forward Radix Sort [Andersson-Nilsson (1994)] D A D A A A C A D A D A A A B D L M C X A A C A W Q D A D A G F G Q P J A C 56

Forward Radix Sort [Andersson-Nilsson (1994)] 1 A A C A D A A A B D L M C X 3 4 5 A A C A W Q C D A D A D A A 9 10 D A G F G Q P J A The strings are partitioned into groups. We keep the starting/end positions of each group. Groups are active or inactive. 57

Forward Radix Sort [Andersson-Nilsson (1994)] 1 A A C A D A 3 A A B D L M C X A A C A W Q 5 C D A 9 D A D A A D A G F G Q P J A The strings are partitioned into groups. We keep the starting/end positions of each group. Groups are active or inactive. 58

Forward Radix Sort [Andersson-Nilsson (1994)] 1 A A C A D A 3 A A B D L M C X A A C A W Q 5 C D A 9 D A D A A D A G F G Q P J A 59

Forward Radix Sort [Andersson-Nilsson (1994)] 1 A A C A D A 3 A A B D L M C X A A C A W Q 5 C D A 9 D A D A A D A G F G Q P J A 60

Forward Radix Sort [Andersson-Nilsson (1994)] A A B D L M C X 2 3 A A C A D A A A C A W Q 6 C D A D A 8 D A D A D A G F G Q P J A 61

Forward Radix Sort [Andersson-Nilsson (1994)] A A B D L M C X 2 3 A A C A D A A A C A W Q 6 C D A D A 8 D A D A D A G F G Q P J A 62

Forward Radix Sort [Andersson-Nilsson (1994)] A A B D L M C X 2 3 A A C A D A A A C A W Q 6 C D A D A 8 D A D A D A G F G Q P J A 63

Forward Radix Sort [Andersson-Nilsson (1994)] A A B D L M C X A A C A D A A A C A W Q C D A D A 7 8 D A D A D A G F G Q P J A 64

Forward Radix Sort [Andersson-Nilsson (1994)] A A B D L M C X A A C A D A A A C A W Q C D A D A 7 8 D A D A D A G F G Q P J A 65

Forward Radix Sort [Andersson-Nilsson (1994)] A A B D L M C X A A C A D A A A C A W Q C D A D A 7 8 D A D A D A G F G Q P J A 66

Forward Radix Sort [Andersson-Nilsson (1994)] A A B D L M C X A A C A D A A A C A W Q C D A D A D A A D A G F G Q P J A 67

Forward Radix Sort [Andersson-Nilsson (1994)] Sequentially scan the items in the active groups. (The buckets are shared by all groups. ) (Each item remembers the group it belongs to. ) “Empty” each active group. Scan the non-empty buckets, in increasing order. Append each item to its group. How do we find the non-empty buckets? 68

Forward Radix Sort (Slight deviation from [Andersson-Nilsson (1994)]) Consider each active group separately. 69

Forward Radix Sort (Slight deviation from [Andersson-Nilsson (1994)]) Having a collection of smaller problems is almost always better. But, in some cases, e. g. , if we want to use naïve bucket sort, with a large initialization cost, having one large problem is better, and in a sense “cleaner”. 70

Forward Radix Sort [Andersson-Nilsson (1994)] Perform two phases. In the first phase, split into sub-groups, but keep the sub-groups in arbitrary order. 71

Forward Radix Sort [Andersson-Nilsson (1994)] After sorting the list, in the second phase, we can run the original algorithm. 72

Forward Radix Sort [Andersson-Nilsson (1994)] 73

Range reduction revisited Using forward radix sort of Andersson and Nilsson, we get an alternative to the range reduction step of Kirkpatrick and Reisch. 74

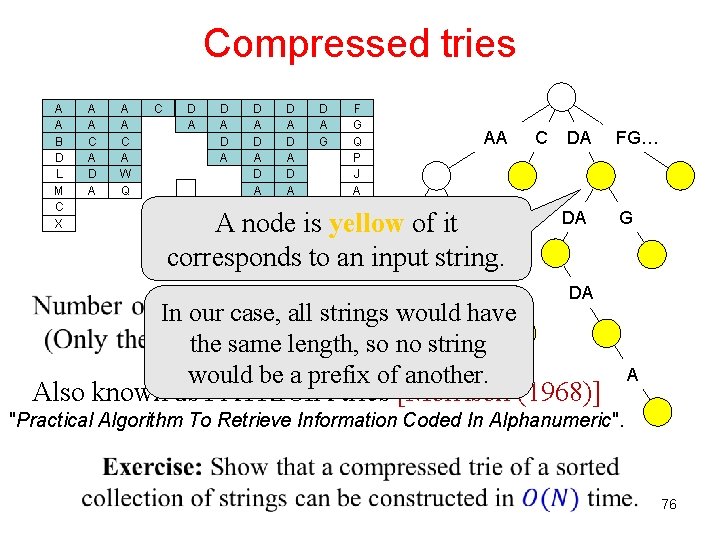
Signature Sort [Andersson-Hagerup-Nilsson-Raman (1998)] Form shortened keys by concatenating the signatures of the parts, and sort them in linear time. Construct a compressed trie of the shortened keys. Sort the edges of the trie, possibly using recursion. The keys now appear in the trie in sorted order. 75

Compressed tries A A B D L M C X A A C A D A A A C A W Q C D A D A D A A D A G F G Q P J A AA A node is yellow. BD… of it. CA corresponds to an input string. DA WQ In our case, all strings would have the same length, so no string would be a prefix of another. C DA DA FG… G DA Also known as PATRICIA tries [Morrison (1968)] A "Practical Algorithm To Retrieve Information Coded In Alphanumeric". 76

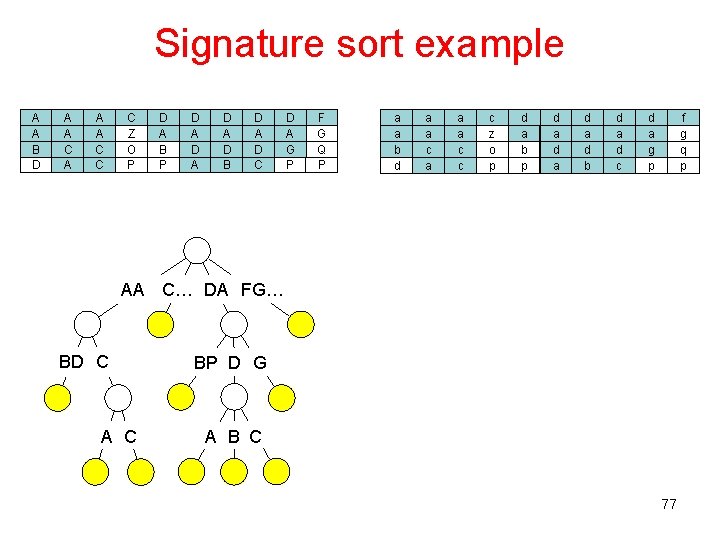
Signature sort example A A B D A A C A A A C C C Z O P D A B P D A D A D B D A D C D A G P F G Q P a a b d a a c a a a c c c z o p d a b p d a d a d b d a d c f g q p d a g p AA C… DA FG… BD C A C BP D G A B C 77

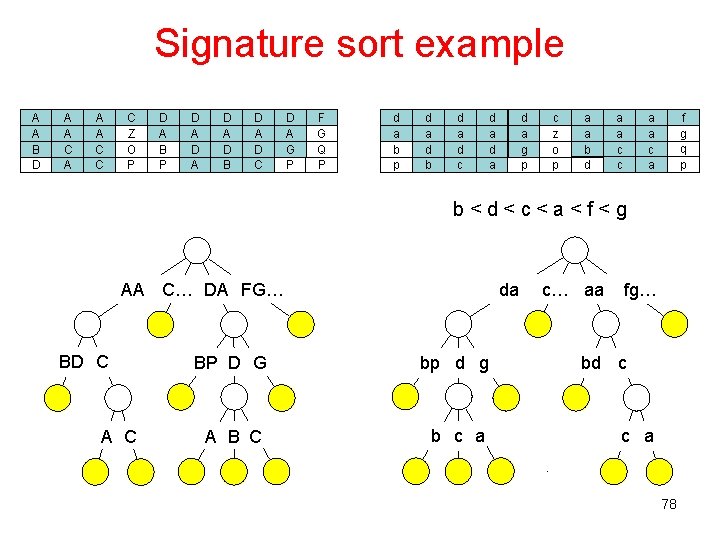
Signature sort example A A B D A A C A A A C C C Z O P D A B P D A D A D B D A D C D A G P F G Q P d a b p d a d b d a d c d a d a g p c z o p a a b d a a c c f g q p a a c a b < d < c < a < f < g da AA C… DA FG… BD C A C BP D G bp d g A B C b c a c… aa fg… bd c c a 78

Signature Sort [Andersson-Hagerup-Nilsson-Raman (1998)] Q: How do we find unique signatures? Q: How do we sort the shortened keys? Q: How do we reorder the trie of the shortened keys to obtain the trie of the original keys? A: Sort the original first character on each edge. If characters are not short enough use recursion. 79

Signature Sort [Andersson-Hagerup-Nilsson-Raman (1998)] As we are only going to repeat it a constant number of times, it does not really matter. Use the trick of finding the minimum edge and not including it in the sort. 80

Signature Sort [Andersson-Hagerup-Nilsson-Raman (1998)] 81

Signature Sort [Andersson-Hagerup-Nilsson-Raman (1998)] 82

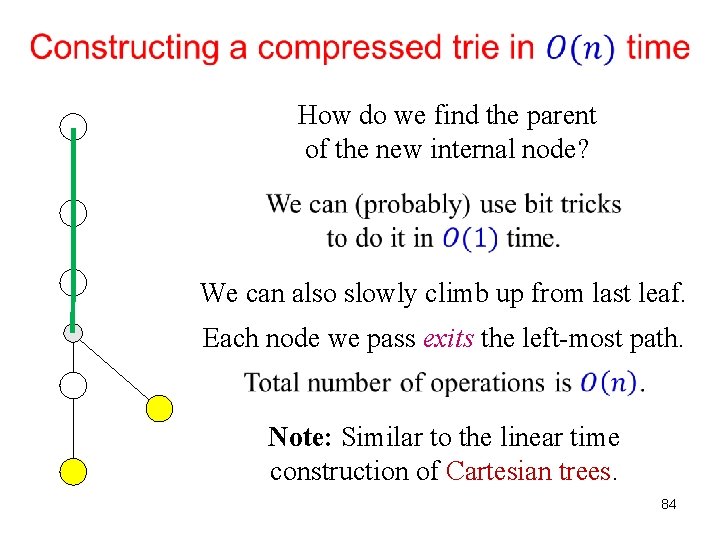
Add the sorted strings to the trie one by one. We may need to add an internal node, unless the common prefix ends at node. How do we find the parent of the new internal node? 83

How do we find the parent of the new internal node? We can also slowly climb up from last leaf. Each node we pass exits the left-most path. Note: Similar to the linear time construction of Cartesian trees. 84

Computing unique signatures [Andersson-Hagerup-Nilsson-Raman (1998)] Really? What do we do if not? Which family of hash functions should we use? 85

Multiplicative hash functions [Dietzfelbinger-Hagerup-Katajainen-Penttonen (1997)] Form an “almost-universal” family Extremely fast in practice! 86