Integer Programming q Formulations Plane scheduling Crew scheduling

Integer Programming (정수계획법) q Formulations Ø Plane scheduling, Crew scheduling leg: one flight taking off from somewhere and landing somewhere else. route: a set of flights that an airplane can serve and return home. Let OR-1 2010 1

Plane scheduling m : total number of legs, n : total number of possible routes (big number). Each route should satisfy timing and regulatory constraints. Assume we already generated enough routes This formulations is a set partitioning type formulation Crew scheduling Crews may ride some airplanes (legs) as passengers. Set covering type formulation. Note that the routes and costs can be different from the plane scheduling case. OR-1 2010 2

Ø Set partitioning, set covering, set packing : N = { 1, 2, 3, 4, 5 } S 1 = {1, 2}, S 2 = {1, 3, 4}, S 3 = {3, 4}, S 4 = { 1, 4, 5}, S 5 = {3, 4, 5}, S 6 = {1, 2, 3}, S 7 = {2, 3} Set partitioning : { S 1, S 5 }, { S 4, S 7 }, … Set covering : { S 1, S 2, S 4 }, { S 4, S 6 }, … Set packing : { S 1, S 3 }, { S 5 }, … OR-1 2010 3

Ø Traveling salesman problem (Formulation in the handout is correct, but not a good formulation. We will consider a different formulation. ) Ø Fixed cost charge problem (Note that y = 1, x = 0 cannot be an optimal solution since K > 0. ) OR-1 2010 4

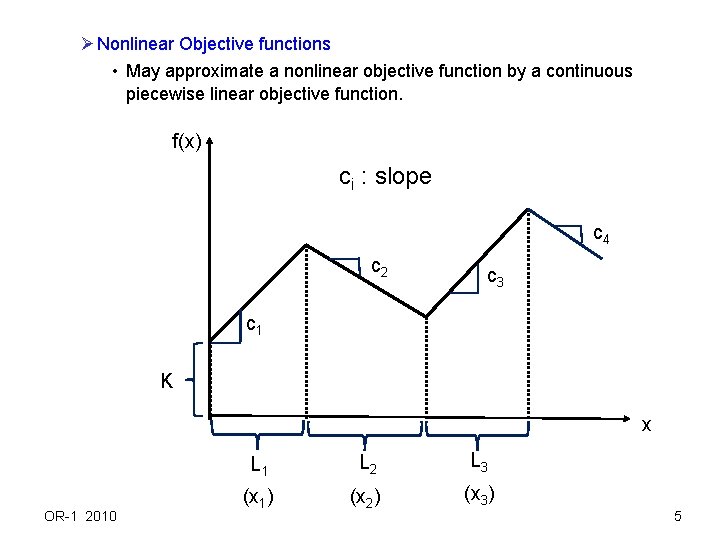
Ø Nonlinear Objective functions • May approximate a nonlinear objective function by a continuous piecewise linear objective function. f(x) ci : slope c 4 c 2 c 3 c 1 K x OR-1 2010 L 1 L 2 L 3 (x 1) (x 2) (x 3) 5

Want to express x as x = L 1 + L 2 + … + Lt-1 + xt and objective value as f(x) = K + c 1 L 1 + c 2 L 2 + … + ct-1 Lt-1 + ctxt. Formulation: Ljwj xj Ljwj-1 w 0 = 1 wj {0, 1} xj 0 j = 1, 2, … , k Ø note that we have wj wj-1 for j = 1, 2, … , k. If wj = 0 for some j wk = 0 for k j+1 If wj = wj-1 = 1 xj = Lj If wj = wj-1 = 0 xj = 0 If wj = 0, wj-1 = 1 0 xj Lj Ø Write the piecewise linear function as K + c 1 x 1 + c 2 x 2 + … + ckxk. OR-1 2010 6

Ø Knapsack problem (general knapsack, binary knapsack problem) Ø either-or constraints If x satisfies at least one of the two constraints, x is feasible. ex) one machine job scheduling problem. M: large value OR-1 2010 7

Ø Functions with N possible values OR-1 2010 8

Ø Quadratic 0 -1 function ex) quadratic knapsack problem max i j cijxixj + djxj Ax b x binary max i j cijyij + djxj Ax b yij xi , yij xj xi + xj – 1 yij x, y binary for all i, j Express xixj by yij and add constraints that ensure yij = 1 if xi = xj = 1, and yij = 0 otherwise. ( If xi = xj = 1 yij = 1, Else (at least one of xi , xj = 0) yij = 0) ( xi = x j = 1 yij = 1 ) OR-1 2010 9

Models with many constraints q Traveling salesman problem (undirected) Undirected graph G = (N, E), edge cost ce , e E N: set of nodes, E: set of edges (edge e = (i, j), i, j N) Find a minimum cost tour that visits each node exactly once and return home Cutset formulation minimize e E ce xe subject to e ({i}) xe = 2 , i N e (S) xe 2 , S N, S , N, xe { 0, 1 }, where (S) = { e = ( i, j ) E : i S, j S} (called a cut defined by S, set of edges with one end node in S and the other end node not in S) OR-1 2010 10

Subtour elimination formulation minimize e E ce xe subject to e ({i}) xe = 2 , e E(S) xe |S| - 1 , xe { 0, 1 }, i N S N, S , N, where E(S) = { e = ( i, j ) E : i S, j S} (set of edges with both end nodes in S) q Both formulations are correct and LP relaxations of both formulations give the same solution set. But there are enormous number of constraints. We will consider how to solve the formulation later. q Although the formulation given in the handout is not a good one, it may be used if we want to solve small TSPs using a generic IP software, not the sophisticated algorithm that can handle the cutset or subtour elimination constraints. OR-1 2010 11

q Integer programming significantly increases the modeling capability, but usually takes much more time to solve than linear programming. Theoretically, it is generally believed that there does not exist a polynomial time algorithm to solve general integer programming problems. However, recent advances in theory and software, combined with powerful computers makes it possible to solve many real world problems using integer programming. OR-1 2010 12