Integer Programming Pendahuluan Dalam penerapannya teknik optimasi sering

Integer Programming

Pendahuluan �Dalam penerapannya, teknik optimasi sering menggunakan variable yang bukan bertipe real, tetapi menggunakan tipe variable yang lain seperti integer atau biner (yang merupakan bagian tipe variable integer) �Dalam kasus seperti ini, bentuk permasalahan optimasi adalah: �Selain fungsi kendala tersebut, dalam proses penyelesaiannya beberapa atau seluruh variable harus bernilai integer non-negatif ( )

Metode Branch and Bound (1) �Terdiri dari beberapa sub-permasalahan, penyelesaian dan analisis keadaan optimal dari setiap sub-permasalahan sampai pada penyelesaian optimal permasalahan utama. �Prinsip metode ini adalah: �Dalam penentuan titik optimal x(0), ada dua keadaan yang terjadi, �Jika x(0) memenuhi semua kendala, maka titik tersebut merupakan penyelesaian sementara dan sub-permasalahan diabaikan. �Jika x(0) tidak memenuhi semua kendala, maka pilih salah satu dari variable berikut ini, � Dan tambahkan ke sub-permasalahan yang ada dan dianalisis pada titik “percabangan” tersebut yang diperoleh dengan menambahkan pada fungsi kendala xi ≤

Metode Branch and Bound (2) �Setelah diperoleh titik penyelesaian sementara x*, sub-permsalahan yang telah diperoleh sebenarnya dianalisis dengan prosedur berikut ini: �Jika cx*≤ cx(0), sub-permasalahan tersebut tidak digunakan lagi, karena tidak menghasilkan nilai penyelesaian yang lebih baik, pilih subpermasalahan yang lain. �Jika cx*> cx(0) dan memenuhi syarat-syarat fungsi kendala secara keseluruhan, x* merupakan penyelesaian sementara yang baru menggantikan x(0) dan sub-permasalahan lainnya dianalisis �Jika cx*> cx(0) dan tidak memenuhi syarat-syarat fungsi kendala secara keseluruhan, buatlah

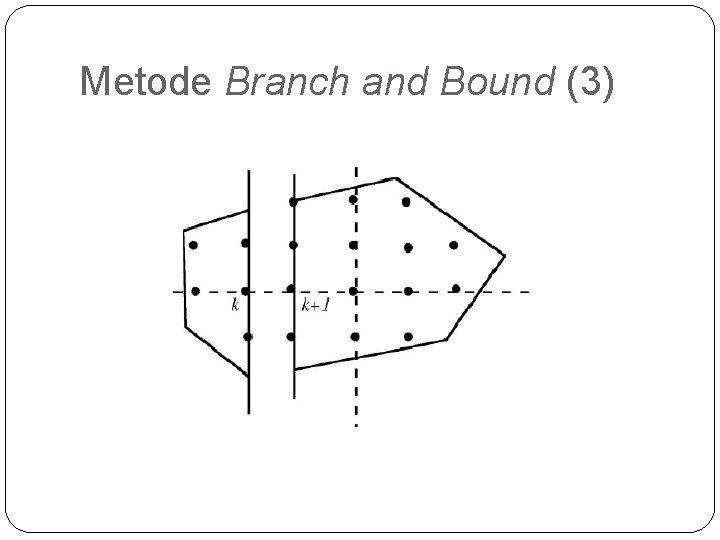
Metode Branch and Bound (3)

Contoh I �Soal: �Minimize Z=3 x 2 + 2 x 3 �Dengan fungsi kendala: � 2 x 1 + 2 x 2 − 4 x 3 = 5 � 4 x 2 + 2 x 3 ≤ 3 �xi ≥ 0, x 1, x 3 ∈ Z (integer)

Penyelesaian Contoh I (1) �Persoalan dengan variable real adalah: �Memiliki titik solusi optimum di (5/2, 0, 0) �Karena x 1 bukan merupakan integer, maka percabangan harus dibuat berdasarkan nilai x 1 tersebut. �Sampai pada tahap ini masih belum diperoleh titik solusi sementara

Penyelesaian Contoh I (2) �Hasil percabangan adalah berupa dua sub- permasalahan berikut ini: �Dan Memiliki titik solusi (2, 1/2, 0) dengan nilai Z = 3/2 Hasil ini memenuhi kendala dan digunakan sebagai titik solusi sementara Memiliki titik solusi (3, 0, 1/4) dengan nilai Z = ½ Titik solusi ini belum memenuhi kendala tetapi nilai Z lebih baik, jadi harus dilakukan percabangan

Penyelesaian Contoh I (3) �Hasil percabangan berikutnya adalah: �Dan Sub-permasalahan ini bersifat infeasible (tidak memiliki solusi) Hal ini disebabkan pada saat nilai x 3 = 0 tidak memenuhi semua kendala. Dengan demikian subpermasalahan ini dihilangkan Memiliki titik solusi (9/2, 0, 1) dengan nilai Z = 2 Hasil nilai Z ini memiliki nilai yang lebih besar dari titik solusi sementara (tidak lebih baik), jadi sub-permasalahan ini dihilangkan

Penyelesaian Contoh I (4) �Dengan demikian, tidak ada lagi sub- permasalahan yang harus dianalisis dan hanya diperoleh satu titik solusi sementara, maka titik solusi sementara tersebut merupakan titik solusi yang optimum dari permasahan pokok. �Jadi penyelesaiannya adalah: �Titik optimum terjadi di titik (2, 1/2, 0) �Dengan nilai Z sebesar 3/2