Integer Programming l Introduction to Integer Programming IP

Integer Programming l Introduction to Integer Programming (IP) l Difficulties of LP relaxation l IP Formulations l Branch and Bound Algorithms 0

Integer Programming Model l An Integer Programming model is a linear programming problem where some or all of the variables are required to be non-negative integers. l These models are in general substantially harder than solving linear programming models. l Network models are special cases of integer programming models and are very efficiently solvable. l We will discuss several applications of integer programming models. l We will study the branch and bound technique, one of the most popular algorithm to solve integer programming models. 1

Classifications of IP Models Pure IP Model: Where all variables must take integer values. Maximize subject to z = 3 x 1 + 2 x 2 x 1 + x 2 £ 6 x 1, x 2 0, x 1 and x 2 integer Mixed IP Model: Where some variables must be integer while others can take real values. Maximize subject to z = 3 x 1 + 2 x 2 x 1 + x 2 £ 6 x 1, x 2 0, x 1 integer 0 -1 IP Model: Where all variables must take values 0 or 1. Maximize subject to z = x 1 - x 2 x 1 + 2 x 2 £ 2 2 x 1 - x 2 £ 1, x 2 = 0 or 1 2

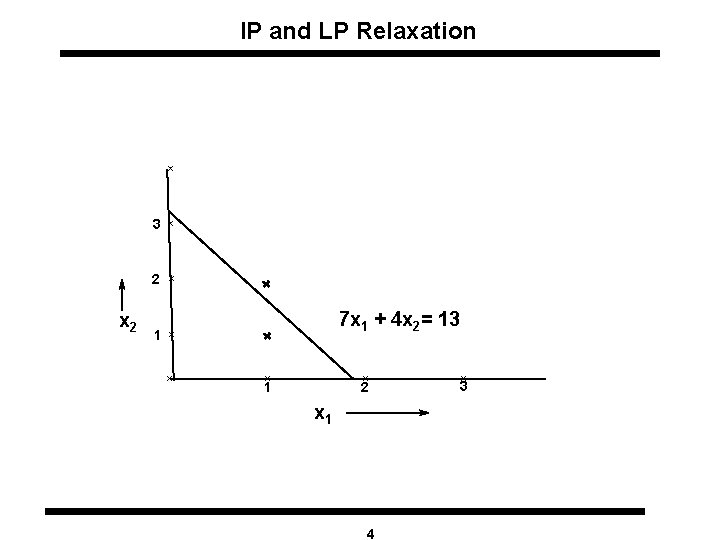
Classifications of IP Models (contd. ) LP Relaxation: The LP obtained by omitting all integer or 0 -1 constraints on variables is called the LP relaxation of IP. IP: Maximize z = 21 x 1 + 11 x 2 subject to 7 x 1 + 4 x 2 £ 13 x 1, x 2 0, x 1 and x 2 integer LP Relaxation: Maximize z = 21 x 1 + 11 x 2 subject to 7 x 1 + 4 x 2 £ 13 x 1, x 2 0 Result: Optimal objective function value of IP £ Optimal objective function value of LP relaxation 3

IP and LP Relaxation x x 2 x 1 7 x 1 + 4 x 2= 13 x x 2 3 x x x 1 2 x 1 4 x 3

Simple Approaches for Solving IP Approach 1: l Enumerate all possible solutions l Determine their objective function values l Select the solution with the maximum (or, minimum) value. Any potential difficulty with this approach? -- may be time-consuming Approach 2: l Solve the LP relaxation l Round-off the solution to the nearest feasible integer solution Any potential difficulty with this approach? -- may not be optimal solution to the original IP 5

The use of binary variables in constraints l Any decision situation that can be modeled by “yes”/“no”, “good”/“bad” etc. , falls into the binary category. l To illustrate 6

The use of binary variables in constraints l Example u A decision is to be made whether each of three plants should be built (Y i = 1) or not built (Yi = 0) Requirement Binary Representation Y 1 + Y 2 +Y 3 2 At least 2 plants must be built If plant 1 is built, plant 2 must not be built Y 1 + Y 2 £ 1 If plant 1 is built, plant 2 must be built Y 1 – Y 2 £ 0 One, but not both plants must be built Y 1+ Y 2 = 1 Both or neither plants must be built Y 1 – Y 2 =0 Plant construction cannot exceed $17 million given the costs to build plants are $5, $8, $10 million 5 Y 1+8 Y 2+10 Y 3 £ 17 7

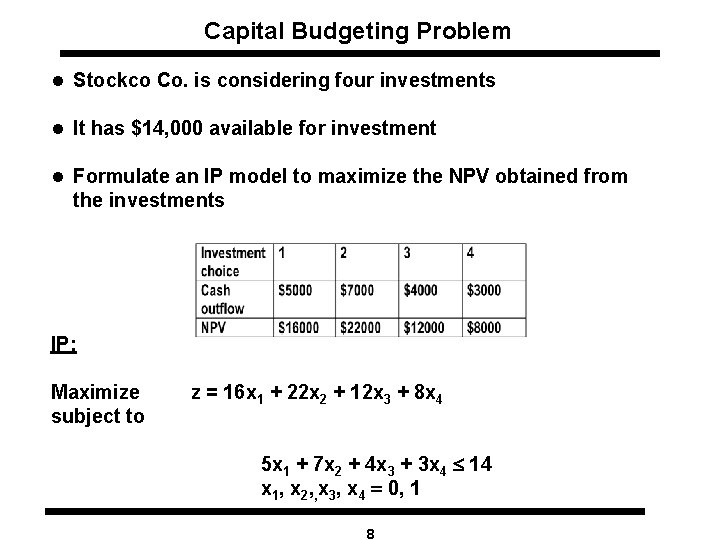
Capital Budgeting Problem l Stockco Co. is considering four investments l It has $14, 000 available for investment l Formulate an IP model to maximize the NPV obtained from the investments IP: Maximize subject to z = 16 x 1 + 22 x 2 + 12 x 3 + 8 x 4 5 x 1 + 7 x 2 + 4 x 3 + 3 x 4 £ 14 x 1, x 2, , x 3, x 4 = 0, 1 8

Fixed Charge Problem l Gandhi cloth company manufactures three types of clothing: shirts, shorts, and pants l Machinery must be rented on a weekly basis to make each type of clothing. Rental Cost: u $200 per week for shirt machinery u $150 per week for shorts machinery u $100 per week for pants machinery l There are 150 hours of labor available per week and 160 square yards of cloth l Find a solution to maximize the weekly profit 9

Fixed Charge Problem (contd. ) Decision Variables: x 1 = number of shirts produced each week x 2 = number of shorts produced each week x 3 = number of pants produced each week y 1 = 1 if shirts are produced and 0 otherwise y 2 = 1 if shorts are produced and 0 otherwise y 3 = 1 if pants are produced and 0 otherwise Formulation: Max. z = 6 x 1 + 4 x 2 + 8 x 3 - 200 y 1 - 150 y 2 - 100 y 3 subject to 3 x 1 + 2 x 2 + 6 x 3 £ 150 4 x 1 + 3 x 2 + 4 x 3 £ 160 x 1 £ M y 1 , x 2 £ M y 2 , x 3 £ M y 3 x 1, x 2, , x 3 0, and integer; y 1, y 2, , y 3 = 0 or 1 10

Either-Or Constraints l Dorian Auto is considering manufacturing three types of auto: compact, midsize, large. l Resources required and profits obtained from these cars are given below. l We have 6, 000 tons of steel and 60, 000 hours of labor available. l If any car is produced, we must produce at least 1, 000 units of that car. l Find a production plan to maximize the profit. 11

Either-Or Constraints (contd. ) Decision Variables: x 1, x 2, x 3 = number of compact, midsize and large cars produced y 1, y 2, y 3 = 1 if compact , midsize and large cars are produced or not Formulation: Maximize z = 2 x 1 + 3 x 2 + 4 x 3 subject to x 1 £ My 1; x 2 £ My 2; x 3 £ My 3 1000 - x 1 1000 - x 2 1000 - x 3 1. 5 x 1 + 3 x 2 + 5 x 3 30 x 1 + 25 x 2 + 40 x 3 £ M(1 -y 1) £ M(1 -y 2) £ M(1 -y 3) £ 60000 x 1, x 2, x 3 0 and integer; y 1, y 2, y 3 = 0 or 1 12

Set Covering Problems l Western Airlines has decided to have hubs in USA. l Western runs flights between the following cities: Atlanta, Boston, Chicago, Denver, Houston, Los Angeles, New Orleans, New York, Pittsburgh, Salt Lake City, San Francisco, and Seattle. l Western needs to have a hub within 1000 miles of each of these cities. l Determine the minimum number of hubs 13

Formulation of Set Covering Problems Decision Variables: xi = 1 if a hub is located in city i xi = 0 if a hub is not located in city i Minimize x. AT + x. BO + x. CH + x. DE + x. HO + x. LA + x. NO + x. NY + x. PI + x. SL + x. SF + x. SE subject to 14

Additional Applications l Location of fire stations needed to cover all cities l Location of fire stations to cover all regions l Truck dispatching problem l Political redistricting l Capital investments 15

Branch and Bound Algorithm l Branch and bound algorithms are the most popular methods for solving integer programming problems l They enumerate the entire solution space but only implicitly; hence they are called implicit enumeration algorithms. l A general-purpose solution technique which must be specialized for individual IP's. l Running time grows exponentially with the problem size, but small to moderate size problems can be solved in reasonable time. 16

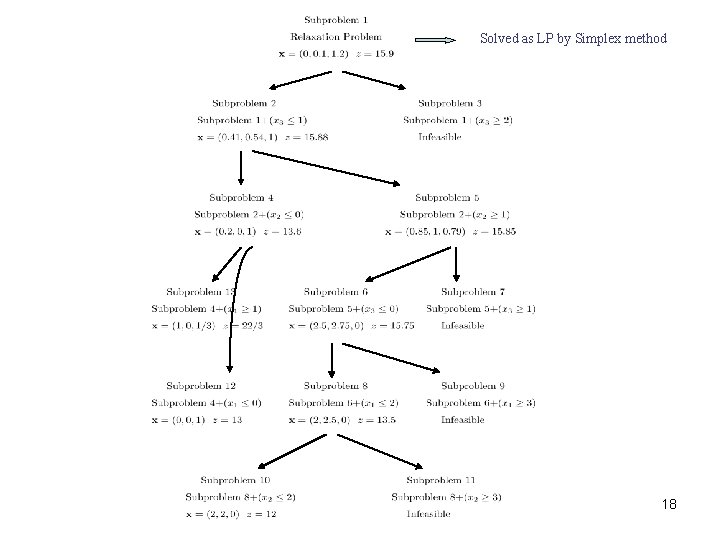
Example: s. t. 17

Solved as LP by Simplex method 18

An Example l Telfa Corporation makes tables and chairs l A table requires one hour of labor and 9 square board feet of wood l A chair requires one hour of labor and 5 square board feet of wood l Each table contributes $8 to profit, and each chair contributes $5 to profit. l 6 hours of labor and 45 square board feet is available l Find a product mix to maximize the profit Maximize z = 8 x 1 + 5 x 2 subject to x 1 + x 2 £ 6; 9 x 1 + 5 x 2 £ 45; x 1, x 2 0; x 1, x 2 integer 19

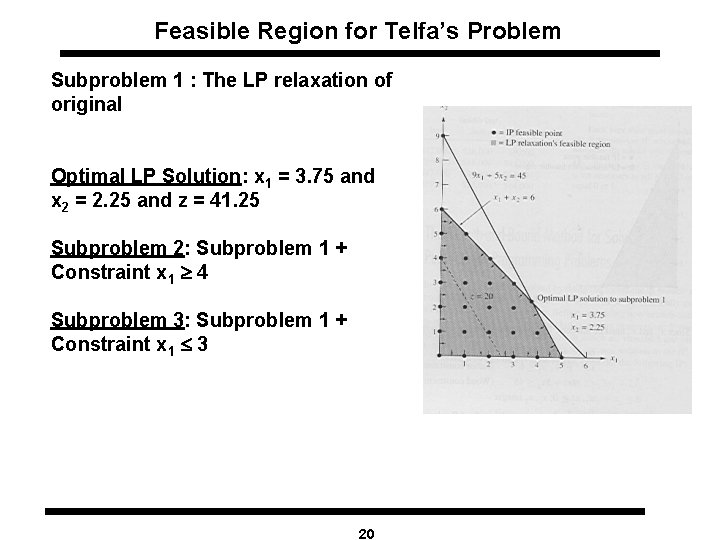
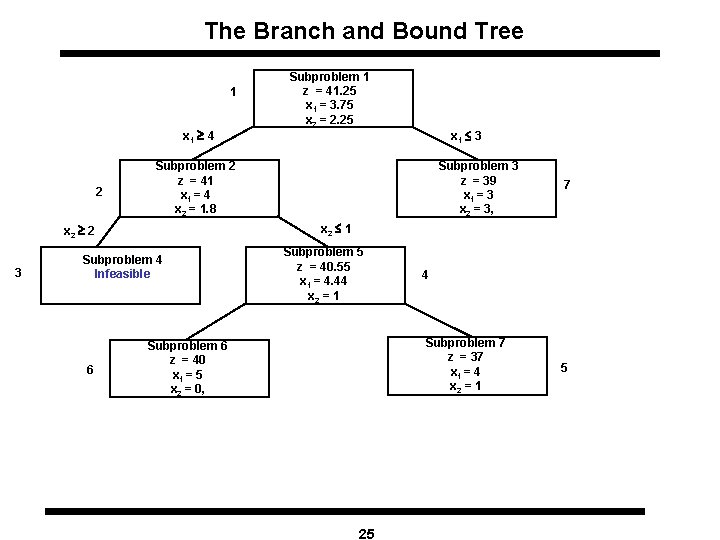
Feasible Region for Telfa’s Problem Subproblem 1 : The LP relaxation of original Optimal LP Solution: x 1 = 3. 75 and x 2 = 2. 25 and z = 41. 25 Subproblem 2: Subproblem 1 + Constraint x 1 4 Subproblem 3: Subproblem 1 + Constraint x 1 £ 3 20

Feasible Region for Subproblems Branching : The process of decomposing a subproblem into two or more subproblems is called branching. Optimal solution of Subproblem 2: z = 41, 1. 8 x 1 = 4, x 2 = 9/5 = Subproblem 4: Subproblem 2 + Constraint x 2 2 Subproblem 5: Subproblem 2 + Constraint x 2 £ 1 21

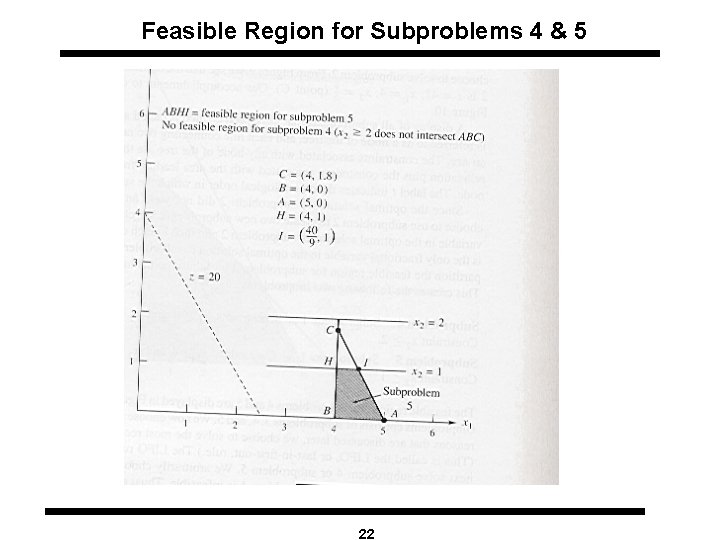
Feasible Region for Subproblems 4 & 5 22

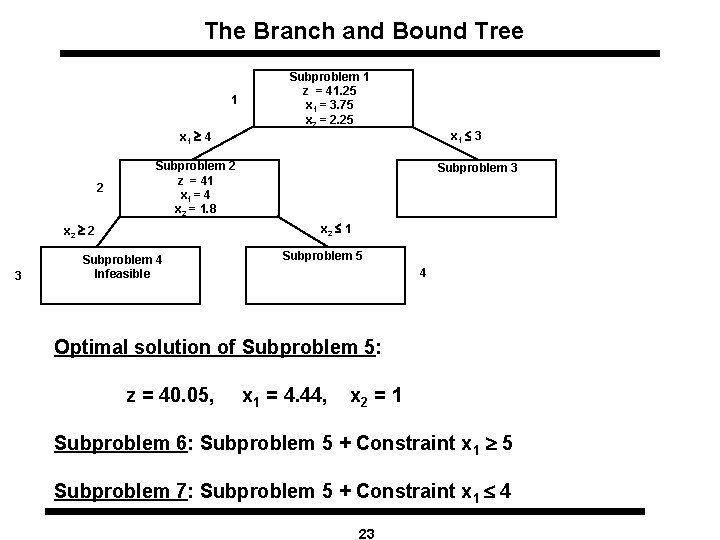
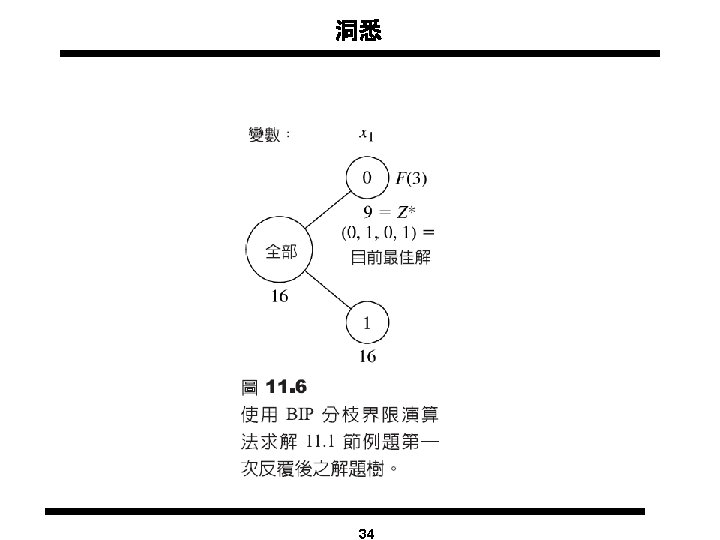
The Branch and Bound Tree 1 Subproblem 1 z = 41. 25 x 1 = 3. 75 x 2 = 2. 25 x 1 £ 3 x 1 4 2 Subproblem 2 z = 41 x 1 = 4 x 2 = 1. 8 x 2 £ 1 x 2 2 3 Subproblem 4 Infeasible Subproblem 5 4 Optimal solution of Subproblem 5: z = 40. 05, x 1 = 4. 44, x 2 = 1 Subproblem 6: Subproblem 5 + Constraint x 1 5 Subproblem 7: Subproblem 5 + Constraint x 1 £ 4 23

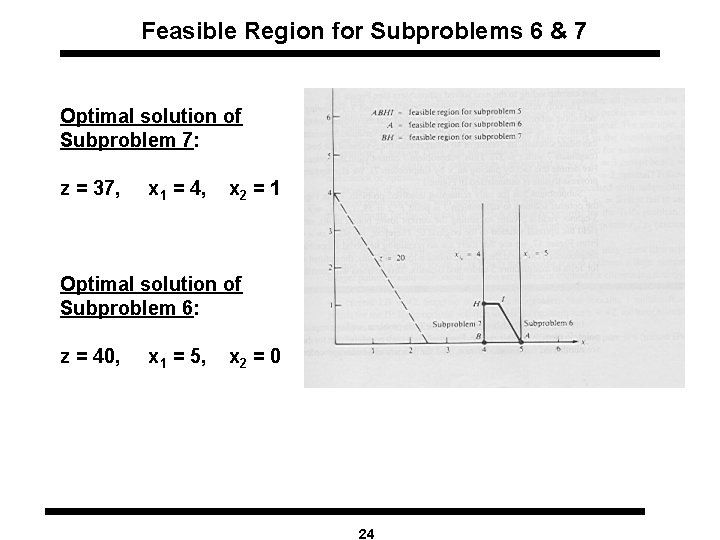
Feasible Region for Subproblems 6 & 7 Optimal solution of Subproblem 7: z = 37, x 1 = 4, x 2 = 1 Optimal solution of Subproblem 6: z = 40, x 1 = 5, x 2 = 0 24

The Branch and Bound Tree 1 x 1 4 2 Subproblem 3 z = 39 x 1 = 3 x 2 = 3, 7 x 2 £ 1 Subproblem 4 Infeasible 6 x 1 £ 3 Subproblem 2 z = 41 x 1 = 4 x 2 = 1. 8 x 2 2 3 Subproblem 1 z = 41. 25 x 1 = 3. 75 x 2 = 2. 25 Subproblem 5 z = 40. 55 x 1 = 4. 44 x 2 = 1 4 Subproblem 7 z = 37 x 1 = 4 x 2 = 1 Subproblem 6 z = 40 x 1 = 5 x 2 = 0, 25 5

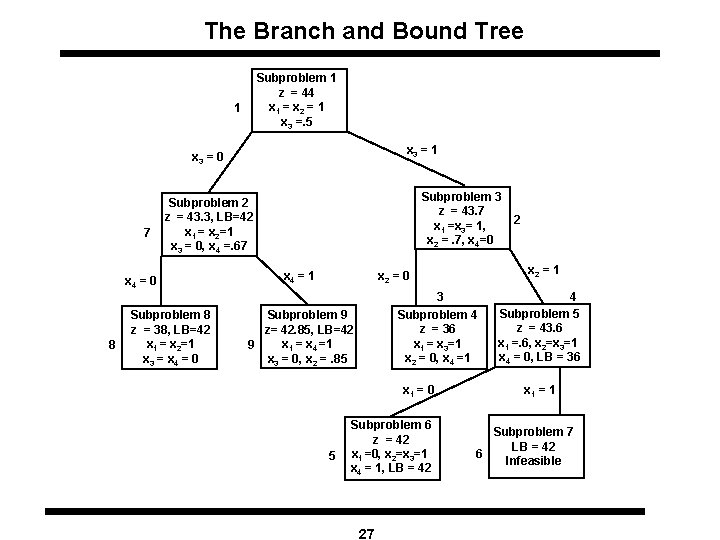
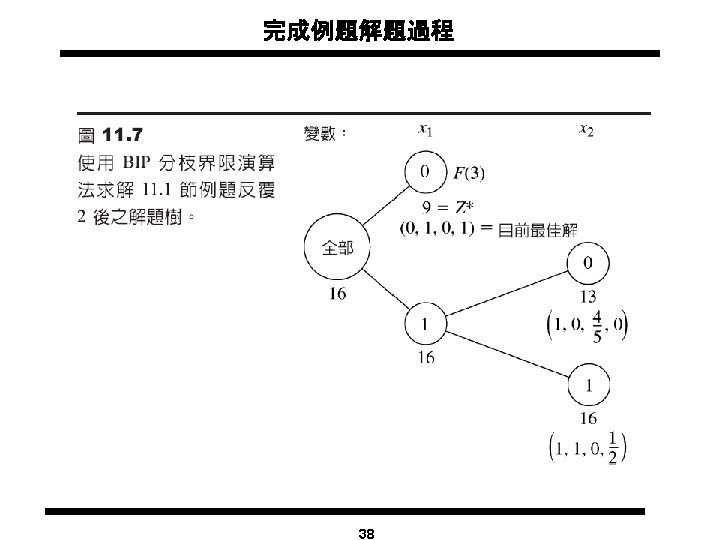
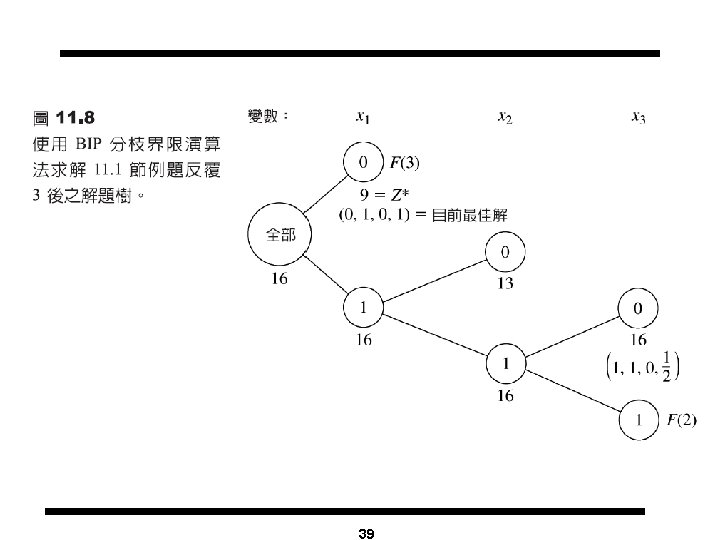
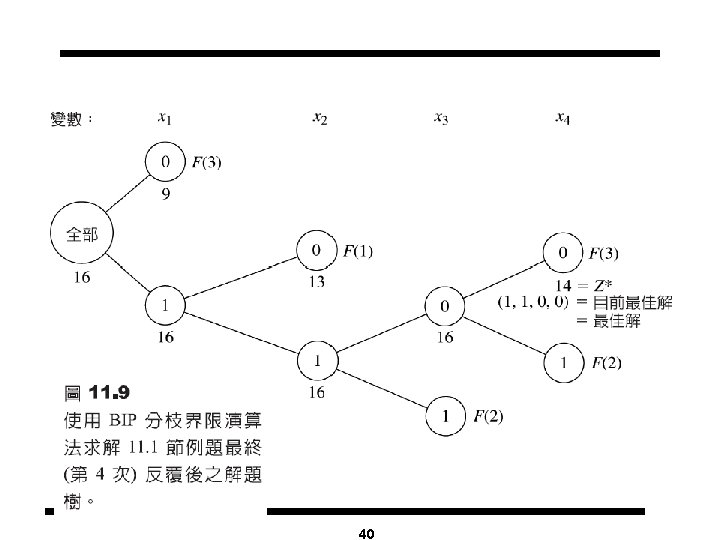
Solving Knapsack Problems Max z = 16 x 1+ 22 x 2 + 12 x 3 + 8 x 4 subject to 5 x 1+ 7 x 2 + 4 x 3 + 3 x 4 £ 14 xi = 0 or 1 for all i = 1, 2, 3, 4 LP Relaxation: Max z = 16 x 1+ 22 x 2 + 12 x 3 + 8 x 4 subject to 5 x 1+ 7 x 2 + 4 x 3 + 3 x 4 £ 14 0 £ xi £ 1 for all i = 1, 2, 3, 4 Solving the LP Relaxation: l Order xi’s in the decreasing order of ci/ai where ci are the cost coefficients and ai’s are the coefficients in the constraint ( Here: x 1→x 2 → x 3 → x 4) l Select items in this order until the constraint is satisfied with equality 26

The Branch and Bound Tree Subproblem 1 z = 44 x 1 = x 2 = 1 x 3 =. 5 1 x 3 = 0 7 x 4 = 0 8 Subproblem 3 z = 43. 7 x 1 =x 3= 1, x 2 =. 7, x 4=0 Subproblem 2 z = 43. 3, LB=42 x 1 = x 2=1 x 3 = 0, x 4 =. 67 Subproblem 8 z = 38, LB=42 x 1 = x 2=1 x 3 = x 4 = 0 x 2 = 1 x 2 = 0 x 4 = 1 3 Subproblem 4 z = 36 x 1 = x 3=1 x 2 = 0, x 4 =1 Subproblem 9 z= 42. 85, LB=42 x 1 = x 4 =1 9 x 3 = 0, x 2 =. 85 x 1 = 0 5 Subproblem 6 z = 42 x 1 =0, x 2=x 3=1 x 4 = 1, LB = 42 27 2 4 Subproblem 5 z = 43. 6 x 1 =. 6, x 2=x 3=1 x 4 = 0, LB = 36 x 1 = 1 Subproblem 7 LB = 42 6 Infeasible

Strategies of Branch and Bound The branch and bound algorithm is a divide and conquer algorithm, where a problem is divided into smaller and smaller subproblems. Each subproblem is solved separately, and the best solution is taken. Lower Bound (LB): Objective function value of the best solution found so far. Branching Strategy : The process of decomposing a subproblem into two or more subproblems is called branching. 28

Strategies of Branch and Bound (contd. ) Upper Bounding Strategy: The process of obtaining an upper bound (UB) for each subproblem is called an upper bounding strategy. Pruning Strategy: If for a subproblem, UB £ LB, then the subproblem need not be explored further. (Illustrate how to fathom nodes in a search tree ) Searching Strategy: The order in which subproblems are examined. Popular search strategies: LIFO and FIFO. 29

37

39

40

44

45

46

47

48

49

50

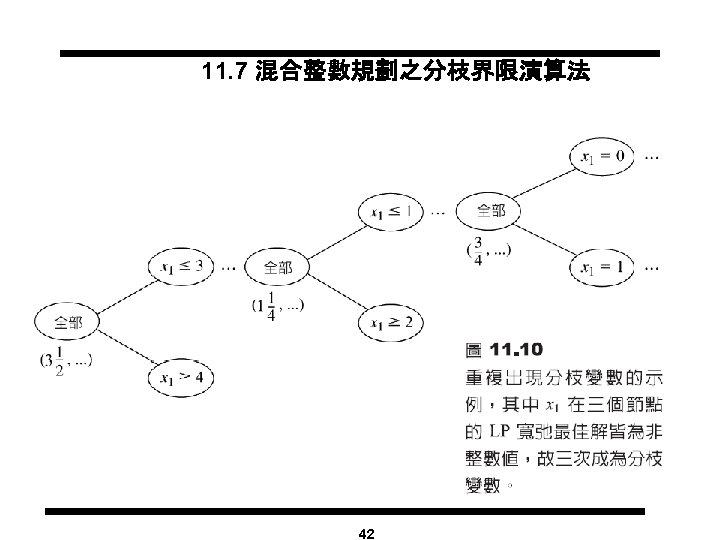
51

52

53