Integer Programming and LogicBased Modeling Jan Fbry Jan

Integer Programming and Logic-Based Modeling Jan Fábry, Jan Pelikán ______________________________________ MME 2003, Prague

Integer Programming Models Discrete variables: NP-hard problems Standard Branch and Bound Method Ø Non-polynomial method (exponential number of branches) Ø Estimation of the optimal objective value ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

Integer Programming Models Reduction of number of branches Ø Skiping non-effective branches (using the estimation of the optimal objective value) Ø Heuristic methods Ø Logic-based Branch and Bound Method ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

TSP – IP Model ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

TSP – Logic-Based Model ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

Integer Knapsack Problem Example: Cost = (5, 8, 4) 3 objects Profit = (3, 5, 2) Feasible (4, 2, 1) Value {1, 2, 3, 4} All different Total profit 30 Infeasible (2, 2, 1) Objective: minimize total cost ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

Integer Knapsack Problem IP model Logic-based model ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

Logic-based Approach Advantage Ø Reduction of branches Ø Simplicity of L-B models Disadvantage Ø No estimation of the optimal value ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

Integer Knapsack Problem Domain VAR x 1 VAR VALUE 2 x 2 VALUE 4 x 3 x 1 1 2 3 4 x 2 1 2 3 4 x 3 1 2 3 4 VAR 3 VALUE x 1 2 x 2 2 x 3 3 ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

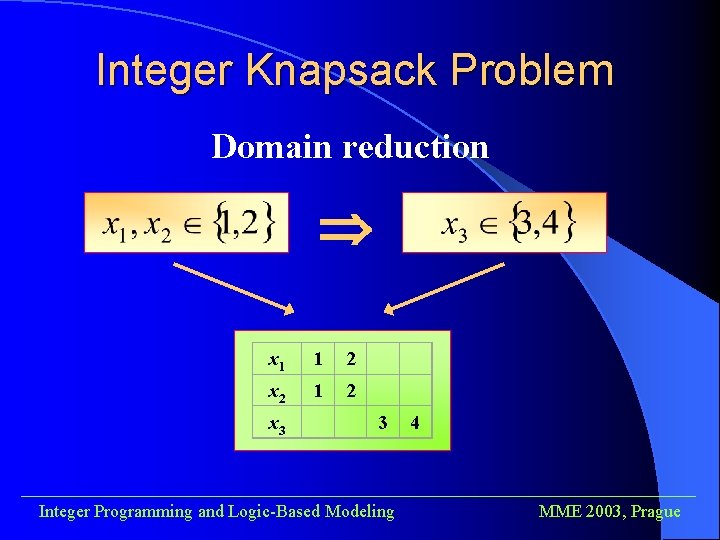
Integer Knapsack Problem Domain reduction x 1 1 2 x 2 1 2 x 3 3 4 ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

Integer Knapsack Problem Bounds consistency maintenance x 1 1 x 2 x 3 1 2 3 4 ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

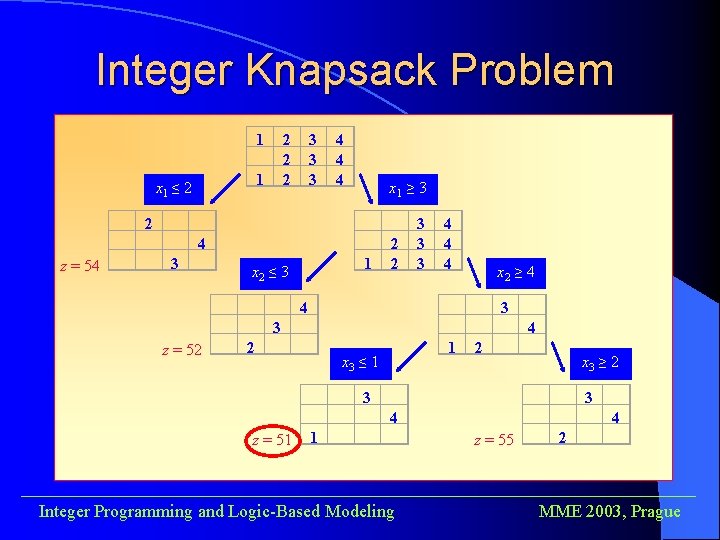
Integer Knapsack Problem 1 1 x 1 ≤ 2 2 3 3 3 4 4 4 x 1 ≥ 3 2 z = 54 4 3 1 x 2 ≤ 3 2 2 3 3 3 4 4 4 x 2 ≥ 4 4 z = 52 3 3 2 1 x 3 ≤ 1 4 2 x 3 ≥ 2 3 z = 51 1 3 4 z = 55 4 2 ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

Logic-Based Modeling Defined predicates all-different {y 1, …, yn} Ø The domains of variables yj may have more than n elements. Ø The constraint requires that variables y 1, …, yn take distinct values. Ø It is mostly used in assignment problems. ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

Logic-Based Modeling Defined predicates circuit (y 1, …, yn) Ø Ø The constraint requires that yj is the integer occurring after j in some permutation of 1, 2, …, n. Ø Used in vehicle routing applications. ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

Logic-Based Modeling Defined predicates path (y 1, …, yk) Ø ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

Logic-Based Modeling Defined predicates distribute ((m 1, …, mn), (x 1, …, xn), a) Ø Ø The constraint requires that value of xj occurs exactly mj times in array a of an arbitrary length. ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

Logic-Based Modeling Defined predicates cumulative ((t 1, …, tn), (d 1, …, dn), (c 1, …, cn), C) Ø Used in job scheduling problems. Ø Variable tj represents the start time of the job j. Ø Parameters dj and cj are the duration and the consuming resource rate of the job j. Ø The resource limit is C. ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

Logic-Based Modeling Defined predicates element (y, (c 1, …, cn), z) Ø The constraint requires that z = cy. Ø y and z are variables. Ø All cj are constants. Ø Used in lot-sizing problems. ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

Software Standard Branch and Bound Method LINGO, AMPL, XPRES-MP, ILOG CPLEX, … Logic-based modeling CHIP V 5, OPBDP, ILOG Solver (OPL Studio), … TRIAL VERSION: http: //www. ilog. com/products/oplstudio/trial. cfm ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

Mathematical Recreation JAN DNES NEVI ZDA SE JEDNA JIZDA ZNOVA enum Letters {J, A, E, N, D, S, V, I, Z, O}; var int k[Letters] in 0. . 9; solve { alldifferent(k) on. Domain; 100*k[J]+10*k[A]+k[N] +1000*k[D]+100*k[N]+10*k[E]+k[S] +1000*k[N]+100*k[E]+10*k[V]+k[I] +100*k[Z]+10*k[D]+k[A] +10*k[S]+k[E] +1000*k[J]+100*k[E]+10*k[D]+k[E] +10000*k[J]+1000*k[E]+100*k[D]+10*k[N]+k[A] +10000*k[J]+1000*k[I]+100*k[Z]+10*k[D]+k[A] =10000*k[Z]+1000*k[N]+100*k[O]+10*k[V]+k[A]; k[J]>=1; k[D]>=1; k[N]>=1; k[Z]>=1; k[S]>=1; [J]<=5; }; ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

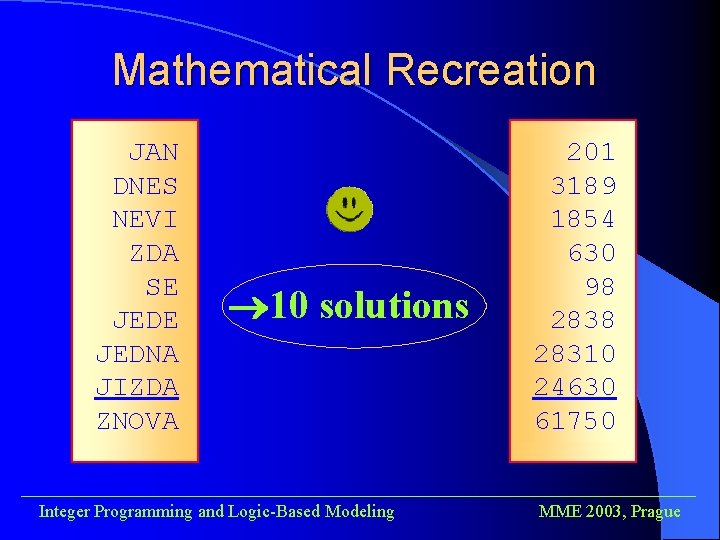
Mathematical Recreation JAN DNES NEVI ZDA SE JEDNA JIZDA ZNOVA 10 solutions 201 3189 1854 630 98 28310 24630 61750 ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague

Questions ______________________________________ Integer Programming and Logic-Based Modeling MME 2003, Prague