Integer Multiplication and Division ICS 233 Computer Architecture

Integer Multiplication and Division ICS 233 Computer Architecture and Assembly Language Dr. Aiman El-Maleh College of Computer Sciences and Engineering King Fahd University of Petroleum and Minerals [Adapted from slides of Dr. M. Mudawar, ICS 233, KFUPM]

Outline v Unsigned Multiplication v Signed Multiplication v Unsigned Division v Signed Division v Multiplication and Division in MIPS Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 2

Unsigned Multiplication v Paper and Pencil Example: Multiplicand Multiplier × 11002 = 12 11012 = 13 1100 0000 1100 Product Binary multiplication is easy 0 × multiplicand = 0 1 × multiplicand = multiplicand 100111002 = 156 v m-bit multiplicand × n-bit multiplier = (m+n)-bit product v Accomplished via shifting and addition Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 3

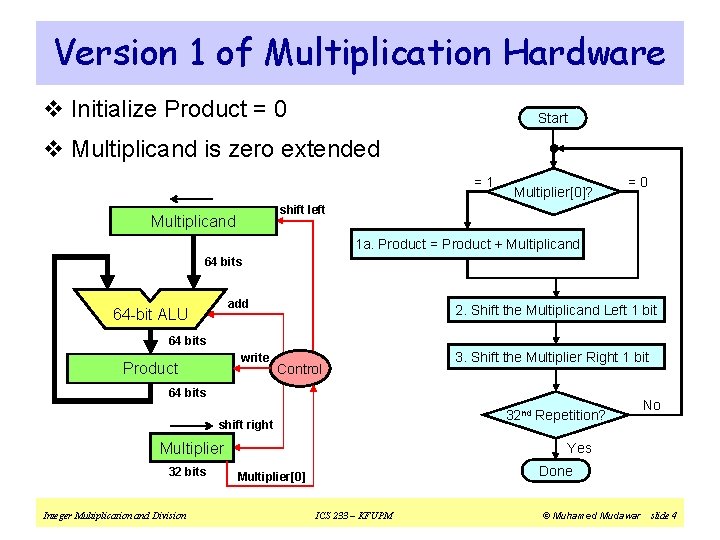
Version 1 of Multiplication Hardware v Initialize Product = 0 Start v Multiplicand is zero extended =1 Multiplier[0]? =0 shift left Multiplicand 1 a. Product = Product + Multiplicand 64 bits add 64 -bit ALU 2. Shift the Multiplicand Left 1 bit 64 bits write Product Control 3. Shift the Multiplier Right 1 bit 64 bits 32 nd Repetition? shift right Multiplier 32 bits Integer Multiplication and Division No Yes Done Multiplier[0] ICS 233 – KFUPM © Muhamed Mudawar slide 4

Multiplication Example (Version 1) v Consider: 11002 × 11012 , Product = 100111002 v 4 -bit multiplicand multiplier are used in this example v Multiplicand is zero extended because it is unsigned Iteration 0 1 2 3 4 Multiplicand Multiplier Initialize 00001100 1101 0000 + 00001100 Multiplier[0] = 1 => ADD SLL Multiplicand SRL Multiplier 00011000 0110 00001100 Multiplier[0] = 0 => Do Nothing SLL Multiplicand SRL Multiplier 00110000 0011 + 00111100 Multiplier[0] = 1 => ADD SLL Multiplicand SRL Multiplier 01100000 0001 + 10011100 Multiplier[0] = 1 => ADD SLL Multiplicand SRL Multiplier Integer Multiplication and Division Product 11000000 ICS 233 – KFUPM 0000 © Muhamed Mudawar slide 5

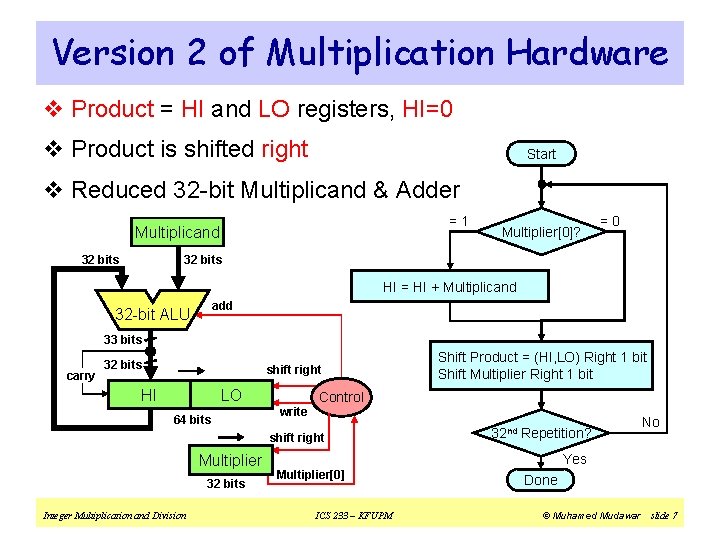
Observation on Version 1 of Multiply v Hardware in version 1 can be optimized v Rather than shifting the multiplicand to the left Instead, shift the product to the right Has the same net effect and produces the same results v Reduce Hardware ² Multiplicand register can be reduced to 32 bits only ² We can also reduce the adder size to 32 bits v One cycle per iteration ² Shifting and addition can be done simultaneously Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 6

Version 2 of Multiplication Hardware v Product = HI and LO registers, HI=0 v Product is shifted right Start v Reduced 32 -bit Multiplicand & Adder =1 Multiplicand 32 bits Multiplier[0]? =0 32 bits HI = HI + Multiplicand add 32 -bit ALU 33 bits carry 32 bits shift right HI LO 64 bits Control write shift right Multiplier 32 bits Integer Multiplication and Division Shift Product = (HI, LO) Right 1 bit Shift Multiplier Right 1 bit 32 nd Repetition? No Yes Multiplier[0] ICS 233 – KFUPM Done © Muhamed Mudawar slide 7

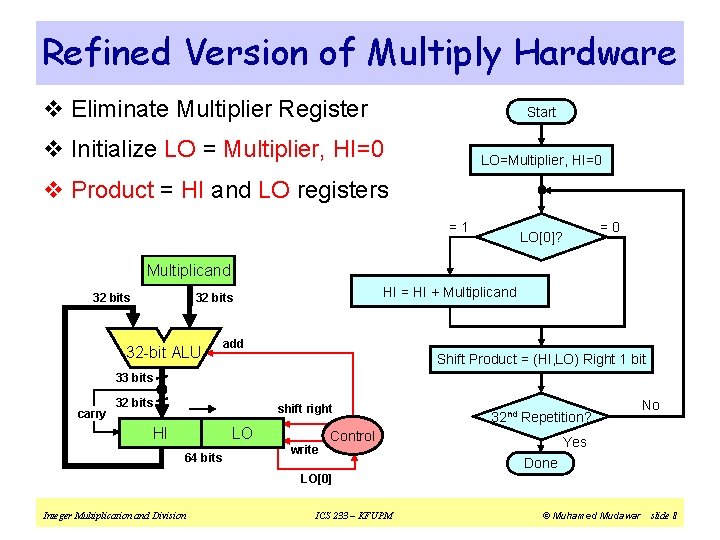
Refined Version of Multiply Hardware v Eliminate Multiplier Register Start v Initialize LO = Multiplier, HI=0 LO=Multiplier, HI=0 v Product = HI and LO registers =1 =0 LO[0]? Multiplicand 32 bits HI = HI + Multiplicand 32 bits 32 -bit ALU add Shift Product = (HI, LO) Right 1 bit 33 bits carry 32 bits shift right HI LO 64 bits 32 nd Repetition? Control write No Yes Done LO[0] Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 8

Multiply Example (Refined Version) v Consider: 11002 × 11012 , Product = 100111002 v 4 -bit multiplicand multiplier are used in this example v 4 -bit adder produces a 5 -bit sum (with carry) Iteration 0 1 2 3 4 Initialize (LO = Multiplier, HI=0) Multiplicand Product = HI, LO 0000 1101 1100 + LO[0] = 1 => ADD Shift Right Product = (HI, LO) Carry 0 1101 1100 0110 1100 0011 LO[0] = 0 => Do Nothing Shift Right Product = (HI, LO) LO[0] = 1 => ADD Shift Right Product = (HI, LO) + + Integer Multiplication and Division 1100 ICS 233 – KFUPM 1111 0011 0111 1001 1100 LO[0] = 1 => ADD Shift Right Product = (HI, LO) 0 1 0011 1001 1100 © Muhamed Mudawar slide 9

Next. . . v Unsigned Multiplication v Signed Multiplication v Unsigned Division v Signed Division v Multiplication and Division in MIPS Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 10

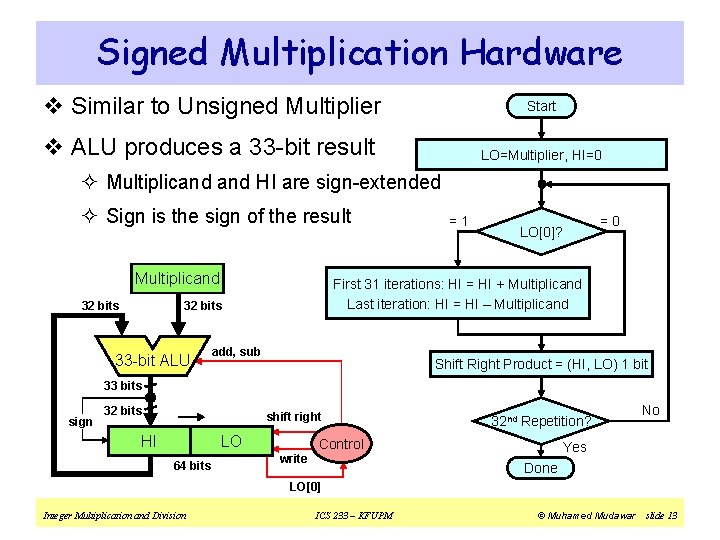
Signed Multiplication v So far, we have dealt with unsigned integer multiplication v Version 1 of Signed Multiplication ² Convert multiplier and multiplicand into positive numbers § If negative then obtain the 2's complement and remember the sign ² Perform unsigned multiplication ² Compute the sign of the product ² If product sign < 0 then obtain the 2's complement of the product v Refined Version: ² Use the refined version of the unsigned multiplication hardware ² When shifting right, extend the sign of the product ² If multiplier is negative, the last step should be a subtract Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 11

Signed Multiplication (Pencil & Paper) v Case 1: Positive Multiplier Multiplicand Multiplier × 11002 = -4 01012 = +5 11111100 Sign-extension Product 111011002 = -20 v Case 2: Negative Multiplier Multiplicand Multiplier × 11002 = -4 11012 = -3 11111100 00100 (2's complement of 1100) Sign-extension Product Integer Multiplication and Division 000011002 = +12 ICS 233 – KFUPM © Muhamed Mudawar slide 12

Signed Multiplication Hardware v Similar to Unsigned Multiplier Start v ALU produces a 33 -bit result LO=Multiplier, HI=0 ² Multiplicand HI are sign-extended ² Sign is the sign of the result Multiplicand 32 bits =0 LO[0]? First 31 iterations: HI = HI + Multiplicand Last iteration: HI = HI – Multiplicand 32 bits 33 -bit ALU =1 add, sub Shift Right Product = (HI, LO) 1 bit 33 bits sign 32 bits shift right HI LO 64 bits 32 nd Repetition? Control write No Yes Done LO[0] Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 13

Signed Multiplication Example v Consider: 11002 (-4) × 11012 (-3), Product = 000011002 v Multiplicand HI are sign-extended before addition v Last iteration: add 2's complement of Multiplicand Iteration 0 1 2 3 4 Multiplicand Initialize (LO = Multiplier) Sign 0000 1101 1100 + LO[0] = 1 => ADD Shift Product = (HI, LO) right 1 bit Product = HI, LO 1 1100 1101 1100 1110 0110 1100 1111 0011 LO[0] = 0 => Do Nothing Shift Product = (HI, LO) right 1 bit LO[0] = 1 => ADD + Shift Product = (HI, LO) right 1 bit 1100 LO[0] = 1 => SUB (ADD 2's compl) 0100 + Shift Product = (HI, LO) right 1 bit Integer Multiplication and Division ICS 233 – KFUPM 1 1011 0011 1101 1001 0 0001 1001 0000 1100 © Muhamed Mudawar slide 14

Next. . . v Unsigned Multiplication v Signed Multiplication v Unsigned Division v Signed Division v Multiplication and Division in MIPS Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 15

Unsigned Division (Paper & Pencil) 100112 = 19 Quotient Divisor 10112 110110012 = 217 -1011 Dividend = Quotient × Divisor + Remainder 217 = 19 × 11 + 8 10 10100 -1011 10011 -1011 Dividend Try to see how big a number can be subtracted, creating a digit of the quotient on each attempt Binary division is accomplished via shifting and subtraction 10002 = 8 Remainder Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 16

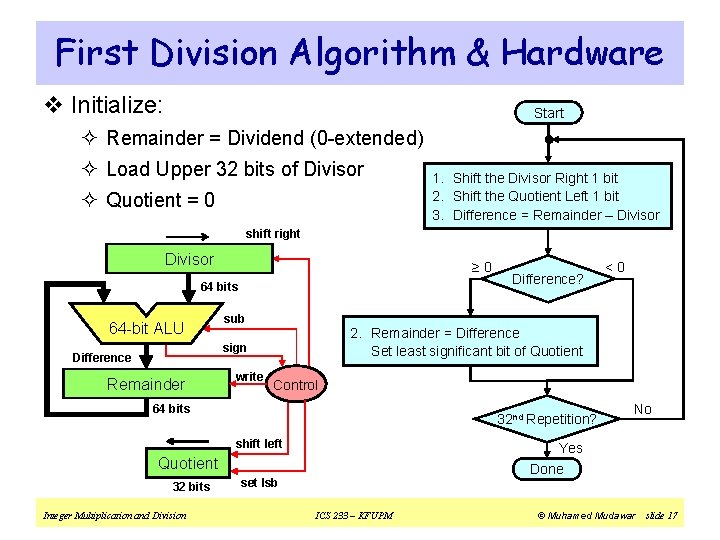
First Division Algorithm & Hardware v Initialize: Start ² Remainder = Dividend (0 -extended) ² Load Upper 32 bits of Divisor ² Quotient = 0 1. Shift the Divisor Right 1 bit 2. Shift the Quotient Left 1 bit 3. Difference = Remainder – Divisor shift right Divisor ≥ 0 64 bits 64 -bit ALU sub 2. Remainder = Difference Set least significant bit of Quotient sign Difference Remainder write Control 64 bits 32 nd Repetition? shift left Integer Multiplication and Division No Yes Quotient 32 bits Difference? <0 Done set lsb ICS 233 – KFUPM © Muhamed Mudawar slide 17

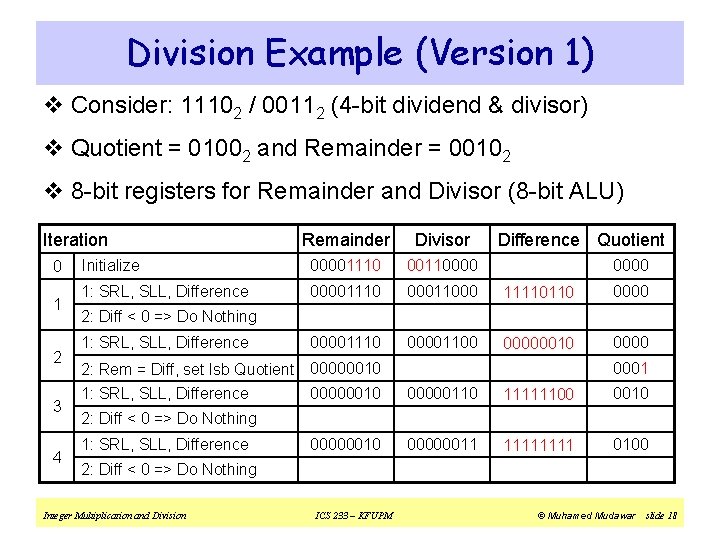
Division Example (Version 1) v Consider: 11102 / 00112 (4 -bit dividend & divisor) v Quotient = 01002 and Remainder = 00102 v 8 -bit registers for Remainder and Divisor (8 -bit ALU) Iteration 0 1 2 3 4 Difference Quotient Remainder Divisor Initialize 00001110 00110000 1: SRL, SLL, Difference 00001110 00011000 11110110 00001110 00001100 00000010 0000 2: Diff < 0 => Do Nothing 1: SRL, SLL, Difference 2: Rem = Diff, set lsb Quotient 00000010 1: SRL, SLL, Difference 00000010 0001 00000110 11111100 0010 00000011 1111 0100 2: Diff < 0 => Do Nothing 1: SRL, SLL, Difference 00000010 2: Diff < 0 => Do Nothing Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 18

Observations on Version 1 of Divide v Version 1 of Division hardware can be optimized v Instead of shifting divisor right, Shift the remainder register left Has the same net effect and produces the same results v Reduce Hardware: ² Divisor register can be reduced to 32 bits (instead of 64 bits) ² ALU can be reduced to 32 bits (instead of 64 bits) ² Remainder and Quotient registers can be combined Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 19

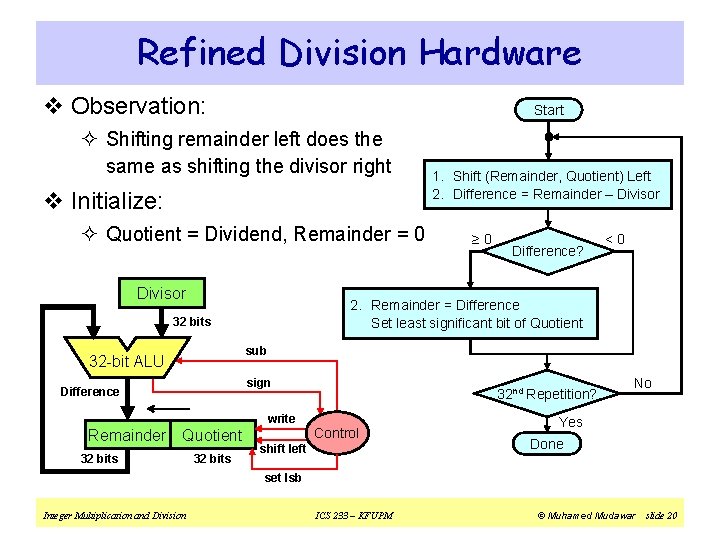
Refined Division Hardware v Observation: Start ² Shifting remainder left does the same as shifting the divisor right v Initialize: ² Quotient = Dividend, Remainder = 0 Divisor ≥ 0 Difference? <0 2. Remainder = Difference Set least significant bit of Quotient 32 bits sub 32 -bit ALU sign Difference write Remainder Quotient 32 bits 1. Shift (Remainder, Quotient) Left 2. Difference = Remainder – Divisor 32 bits 32 nd Repetition? Control shift left No Yes Done set lsb Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 20

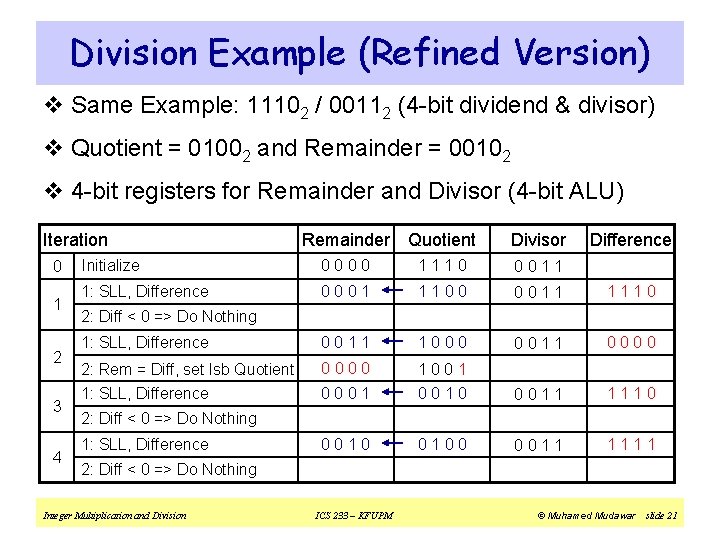
Division Example (Refined Version) v Same Example: 11102 / 00112 (4 -bit dividend & divisor) v Quotient = 01002 and Remainder = 00102 v 4 -bit registers for Remainder and Divisor (4 -bit ALU) Iteration 0 1 2 3 4 Remainder Quotient Divisor Difference Initialize 0000 1110 0011 1: SLL, Difference 0001 1100 0011 1110 1: SLL, Difference 0011 1000 0011 0000 2: Rem = Diff, set lsb Quotient 1: SLL, Difference 0000 0001 1001 0010 0011 1110 0010 0100 0011 1111 2: Diff < 0 => Do Nothing 1: SLL, Difference 2: Diff < 0 => Do Nothing Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 21

Next. . . v Unsigned Multiplication v Signed Multiplication v Unsigned Division v Signed Division v Multiplication and Division in MIPS Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 22

Signed Division v Simplest way is to remember the signs v Convert the dividend and divisor to positive ² Obtain the 2's complement if they are negative v Do the unsigned division v Compute the signs of the quotient and remainder ² Quotient sign = Dividend sign XOR Divisor sign ² Remainder sign = Dividend sign v Negate the quotient and remainder if their sign is negative ² Obtain the 2's complement to convert them to negative Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 23

Signed Division Examples 1. Positive Dividend and Positive Divisor ² Example: +17 / +3 Quotient = +5 Remainder = +2 2. Positive Dividend and Negative Divisor ² Example: +17 / – 3 Quotient = – 5 Remainder = +2 3. Negative Dividend and Positive Divisor ² Example: – 17 / +3 Quotient = – 5 Remainder = – 2 4. Negative Dividend and Negative Divisor ² Example: – 17 / – 3 Quotient = +5 Remainder = – 2 The following equation must always hold: Dividend = Quotient × Divisor + Remainder Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 24

Next. . . v Unsigned Multiplication v Signed Multiplication v Unsigned Division v Signed Division v Multiplication and Division in MIPS Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 25

Multiplication in MIPS v Two Multiply instructions ² mult $s 1, $s 2 ² multu $s 1, $s 2 Signed multiplication Unsigned multiplication v 32 -bit multiplication produces a 64 -bit Product $0 $1 v Separate pair of 32 -bit registers . . ² HI = high-order 32 -bit $31 ² LO = low-order 32 -bit Multiply ² Result of multiplication is always in HI & LO v Moving data from HI/LO to MIPS registers Divide HI LO ² mfhi Rd (move from HI to Rd) ² mflo Rd (move from LO to Rd) Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 26

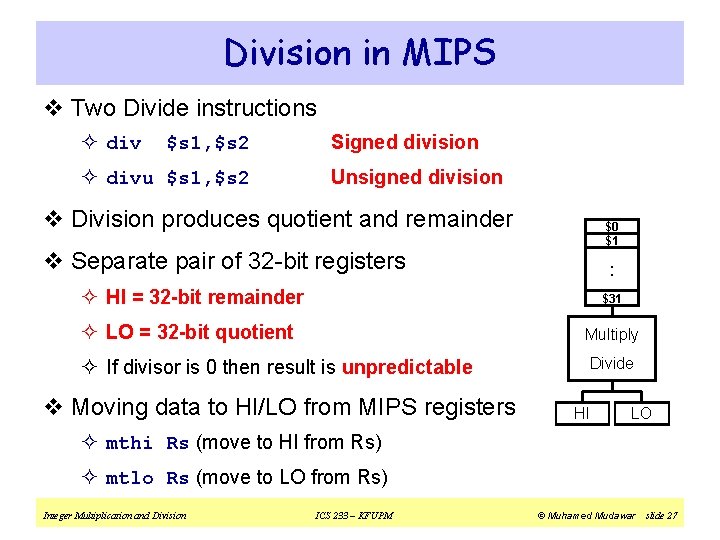
Division in MIPS v Two Divide instructions ² div $s 1, $s 2 ² divu $s 1, $s 2 Signed division Unsigned division v Division produces quotient and remainder $0 $1 v Separate pair of 32 -bit registers . . ² HI = 32 -bit remainder $31 ² LO = 32 -bit quotient Multiply ² If divisor is 0 then result is unpredictable v Moving data to HI/LO from MIPS registers Divide HI LO ² mthi Rs (move to HI from Rs) ² mtlo Rs (move to LO from Rs) Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 27

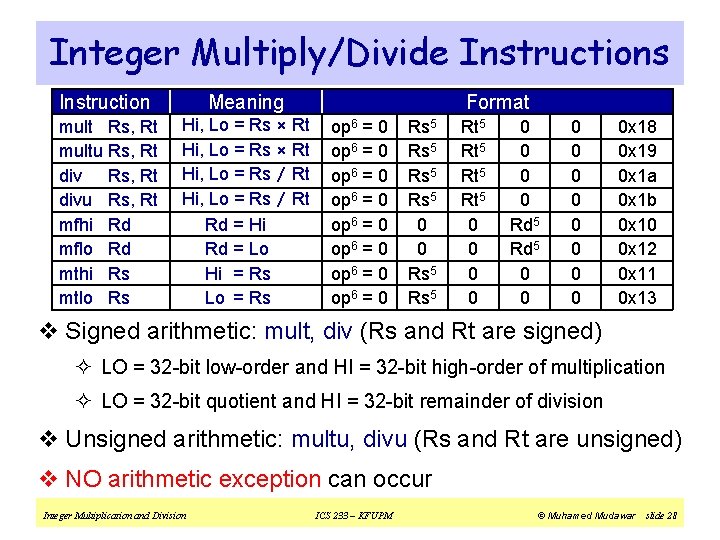
Integer Multiply/Divide Instructions Instruction multu divu mfhi mflo mthi mtlo Rs, Rt Rd Rd Rs Rs Meaning Hi, Lo = Rs × Rt Hi, Lo = Rs / Rt Rd = Hi Rd = Lo Hi = Rs Lo = Rs Format op 6 = 0 op 6 = 0 Rs 5 0 0 Rs 5 Rt 5 0 0 0 0 Rd 5 0 0 0 x 18 0 x 19 0 x 1 a 0 x 1 b 0 x 10 0 x 12 0 x 11 0 x 13 v Signed arithmetic: mult, div (Rs and Rt are signed) ² LO = 32 -bit low-order and HI = 32 -bit high-order of multiplication ² LO = 32 -bit quotient and HI = 32 -bit remainder of division v Unsigned arithmetic: multu, divu (Rs and Rt are unsigned) v NO arithmetic exception can occur Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 28

Integer to String Conversion v Objective: convert an unsigned 32 -bit integer to a string v How to obtain the decimal digits of the number? ² Divide the number by 10, Remainder = decimal digit (0 to 9) ² Convert decimal digit into its ASCII representation ('0' to '9') ² Repeat the division until the quotient becomes zero ² Digits are computed backwards from least to most significant v Example: convert 2037 to a string ² Divide 2037/10 quotient = 203 remainder = 7 char = '7' ² Divide 203/10 quotient = 20 remainder = 3 char = '3' ² Divide 20/10 quotient = 2 remainder = 0 char = '0' ² Divide 2/10 quotient = 0 remainder = 2 char = '2' Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 29

Integer to String Procedure #----------------------------# int 2 str: Converts an unsigned integer into a string # Parameters: $a 0 = integer to be converted # $a 1 = string pointer (can store 10 digits) #----------------------------int 2 str: move $t 0, $a 0 # $t 0 = dividend = integer value li $t 1, 10 # $t 1 = divisor = 10 addiu $a 1, 10 # start at end of string sb $zero, 0($a 1) # store a NULL byte convert: divu $t 0, $t 1 # LO = quotient, HI = remainder mflo $t 0 # $t 0 = quotient mfhi $t 2 # $t 2 = remainder ori $t 2, 0 x 30 # convert digit to a character addiu $a 1, -1 # point to previous char sb $t 2, 0($a 1) # store digit character bnez $t 0, convert # loop if quotient is not 0 jr $ra Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar slide 30