Integer Multiplication and Division ICS 233 Computer Architecture

Integer Multiplication and Division ICS 233 Computer Architecture & Assembly Language Prof. Muhamed Mudawar College of Computer Sciences and Engineering King Fahd University of Petroleum and Minerals

Presentation Outline v Unsigned Integer Multiplication v Signed Integer Multiplication v Faster Integer Multiplication v Integer Division v Integer Multiplication and Division in MIPS Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 2

Unsigned Integer Multiplication v Paper and Pencil Example: Multiplicand Multiplier × 11002 = 12 11012 = 13 1100 0000 1100 Product Binary multiplication is easy 0 × multiplicand = 0 1 × multiplicand = multiplicand 100111002 = 156 v m-bit multiplicand × n-bit multiplier = (m+n)-bit product v Accomplished via shifting and addition v Consumes more time and more chip area than addition Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 3

Sequential Unsigned Multiplication v Initialize Product = 0 v Check each bit of the Multiplier v If Multiplier bit = 1 then Product = Product + Multiplicand v Rather than shifting the multiplicand to the left Instead, Shift the Product to the Right Has the same net effect and produces the same result Minimizes the hardware resources v One cycle per iteration (for each bit of the Multiplier) ² Addition and shifting can be done simultaneously Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 4

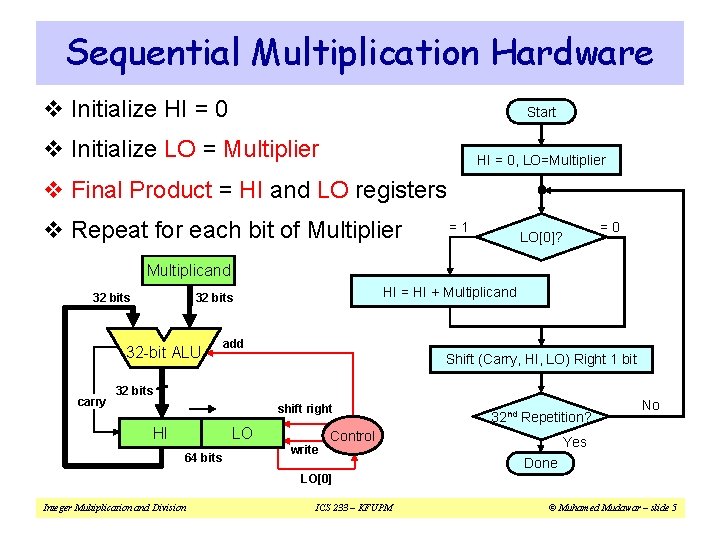
Sequential Multiplication Hardware v Initialize HI = 0 Start v Initialize LO = Multiplier HI = 0, LO=Multiplier v Final Product = HI and LO registers v Repeat for each bit of Multiplier =1 =0 LO[0]? Multiplicand 32 bits 32 -bit ALU carry HI = HI + Multiplicand 32 bits add Shift (Carry, HI, LO) Right 1 bit 32 bits shift right HI LO 64 bits 32 nd Repetition? Control write No Yes Done LO[0] Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 5

Sequential Multiplier Example v Consider: 11002 × 11012 , Product = 100111002 v 4 -bit multiplicand multiplier are used in this example v 4 -bit adder produces a 5 -bit sum (with carry) Iteration 0 1 2 3 4 Multiplicand Initialize (HI = 0, LO = Multiplier) Carry 0000 1101 1100 + LO[0] = 1 => ADD Shift Right (Carry, HI, LO) by 1 bit Product = HI, LO 0 1101 1100 0110 1100 0011 LO[0] = 0 => Do Nothing Shift Right (Carry, HI, LO) by 1 bit LO[0] = 1 => ADD + Shift Right (Carry, HI, LO) by 1 bit + Integer Multiplication and Division 1100 ICS 233 – KFUPM 1111 0011 0111 1001 1100 LO[0] = 1 => ADD Shift Right (Carry, HI, LO) by 1 bit 0 1 0011 1001 1100 © Muhamed Mudawar – slide 6

Next. . . v Unsigned Integer Multiplication v Signed Integer Multiplication v Faster Integer Multiplication v Integer Division v Integer Multiplication and Division in MIPS Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 7

Signed Integer Multiplication v So far, we have dealt with unsigned integer multiplication v First Attempt: ² Convert multiplier and multiplicand into positive numbers § If negative then obtain the 2's complement and remember the sign ² Perform unsigned multiplication ² Compute the sign of the product ² If product sign < 0 then obtain the 2's complement of the product v Better Version: ² Use the unsigned multiplication hardware ² When shifting right, extend the sign of the product ² If multiplier is negative, the last step should be a subtract Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 8

Signed Multiplication (Pencil & Paper) v Case 1: Positive Multiplier Multiplicand Multiplier × 11002 = -4 01012 = +5 Sign-extension 11111100 Product 111011002 = -20 v Case 2: Negative Multiplier Multiplicand Multiplier Sign-extension Product Integer Multiplication and Division × 11002 = -4 11012 = -3 11111100 00100 (2's complement of 1100) 000011002 = +12 ICS 233 – KFUPM © Muhamed Mudawar – slide 9

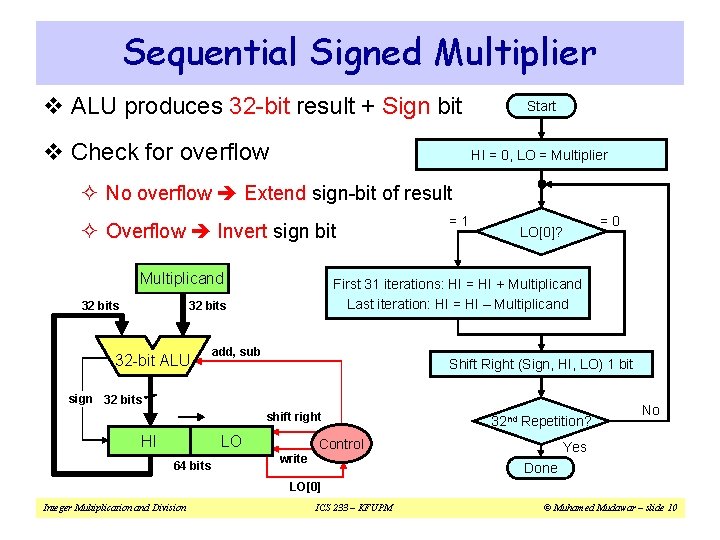
Sequential Signed Multiplier v ALU produces 32 -bit result + Sign bit v Check for overflow Start HI = 0, LO = Multiplier ² No overflow Extend sign-bit of result ² Overflow Invert sign bit Multiplicand 32 bits =0 LO[0]? First 31 iterations: HI = HI + Multiplicand Last iteration: HI = HI – Multiplicand 32 bits 32 -bit ALU =1 add, sub Shift Right (Sign, HI, LO) 1 bit sign 32 bits shift right HI LO 64 bits 32 nd Repetition? Control write No Yes Done LO[0] Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 10

Signed Multiplication Example v Consider: 11002 (-4) × 11012 (-3), Product = 000011002 v Check for overflow: No overflow Extend sign bit v Last iteration: add 2's complement of Multiplicand Iteration 0 1 2 3 4 Multiplicand Initialize (HI = 0, LO = Multiplier) Sign 0000 1101 1100 + LO[0] = 1 => ADD Shift (Sign, HI, LO) right 1 bit Product = HI, LO 1 1100 1101 1100 1110 0110 1100 1111 0011 LO[0] = 0 => Do Nothing Shift (Sign, HI, LO) right 1 bit LO[0] = 1 => ADD + Shift (Sign, HI, LO) right 1 bit 1100 LO[0] = 1 => SUB (ADD 2's compl) 0100 + 1011 0011 1101 1001 0 0001 1001 0000 1100 Shift (Sign, HI, LO) right 1 bit Integer Multiplication and Division 1 ICS 233 – KFUPM © Muhamed Mudawar – slide 11

Next. . . v Unsigned Integer Multiplication v Signed Integer Multiplication v Faster Integer Multiplication v Integer Division v Integer Multiplication and Division in MIPS Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 12

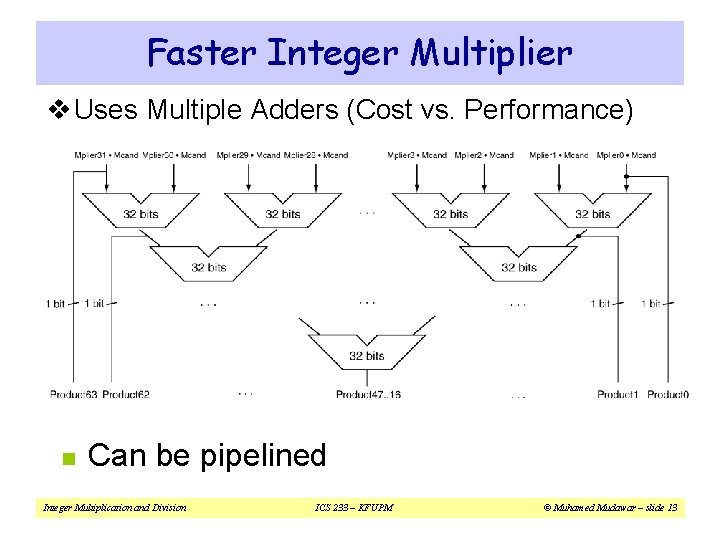
Faster Integer Multiplier v Uses Multiple Adders (Cost vs. Performance) n Can be pipelined Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 13

Using Multiple Adders v 32 -bit adder for each bit of the multiplier ² AND multiplicand with each bit of multiplier ² Product = accumulated shifted sum v Each adder produces a 33 -bit output ² Most significant bit is a carry bit v Array multiplier can be optimized ² Additions can be done in parallel ² Multiple-level tree reduction to produce final product ² Carry save adders reduce delays Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 14

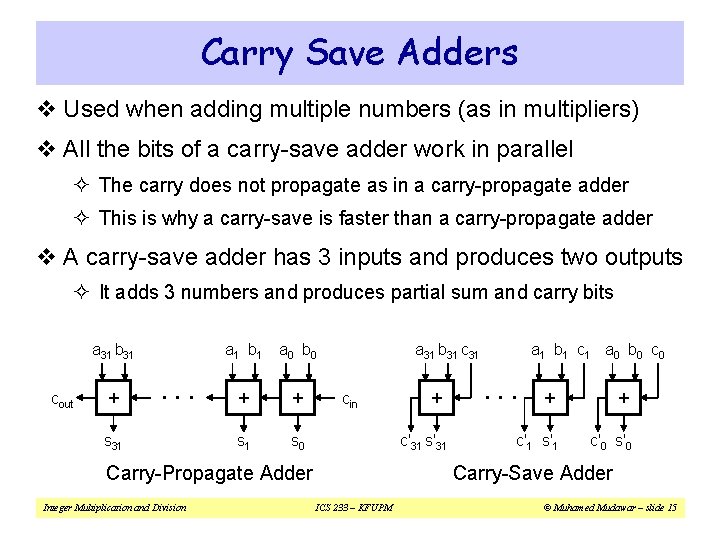
Carry Save Adders v Used when adding multiple numbers (as in multipliers) v All the bits of a carry-save adder work in parallel ² The carry does not propagate as in a carry-propagate adder ² This is why a carry-save is faster than a carry-propagate adder v A carry-save adder has 3 inputs and produces two outputs ² It adds 3 numbers and produces partial sum and carry bits a 31 b 31 cout + . . . s 31 a 1 b 1 a 0 b 0 + + s 1 s 0 a 31 b 31 cin c'31 s'31 Carry-Propagate Adder Integer Multiplication and Division + a 1 b 1 c 1 a 0 b 0 c 0 . . . + + c'1 s'1 c'0 s'0 Carry-Save Adder ICS 233 – KFUPM © Muhamed Mudawar – slide 15

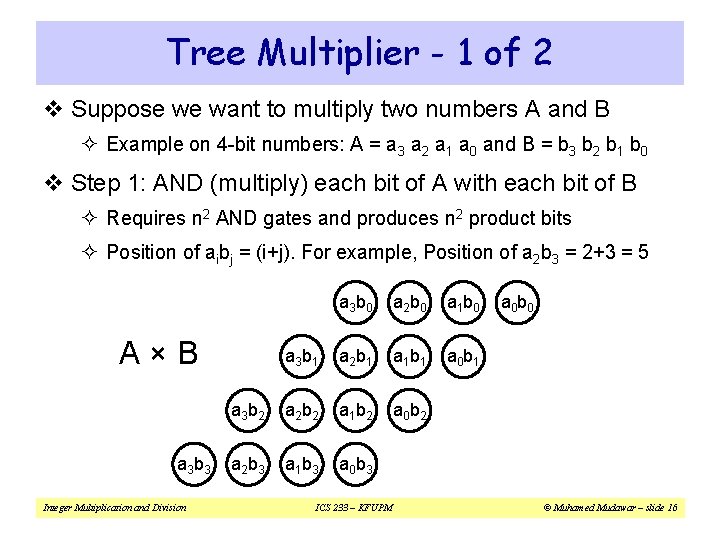
Tree Multiplier - 1 of 2 v Suppose we want to multiply two numbers A and B ² Example on 4 -bit numbers: A = a 3 a 2 a 1 a 0 and B = b 3 b 2 b 1 b 0 v Step 1: AND (multiply) each bit of A with each bit of B ² Requires n 2 AND gates and produces n 2 product bits ² Position of aibj = (i+j). For example, Position of a 2 b 3 = 2+3 = 5 a 3 b 0 a 2 b 0 a 1 b 0 a 3 b 1 a 2 b 1 a 1 b 1 a 0 b 1 a 3 b 2 a 2 b 2 a 1 b 2 a 0 b 2 a 2 b 3 a 1 b 3 a 0 b 3 A×B a 3 b 3 Integer Multiplication and Division ICS 233 – KFUPM a 0 b 0 © Muhamed Mudawar – slide 16

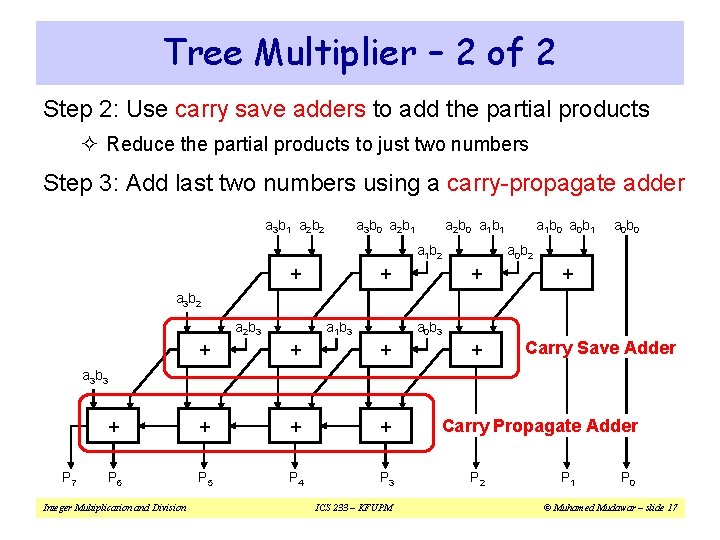
Tree Multiplier – 2 of 2 Step 2: Use carry save adders to add the partial products ² Reduce the partial products to just two numbers Step 3: Add last two numbers using a carry-propagate adder a 3 b 1 a 2 b 2 a 3 b 0 a 2 b 1 a 2 b 0 a 1 b 1 a 1 b 2 + + a 1 b 0 a 0 b 1 a 0 b 0 a 0 b 2 + + a 3 b 2 a 2 b 3 a 1 b 3 a 0 b 3 + + + + P 6 P 5 P 4 P 3 + Carry Save Adder a 3 b 3 P 7 Integer Multiplication and Division ICS 233 – KFUPM Carry Propagate Adder P 2 P 1 P 0 © Muhamed Mudawar – slide 17

Next. . . v Unsigned Integer Multiplication v Signed Integer Multiplication v Faster Integer Multiplication v Integer Division v Integer Multiplication and Division in MIPS Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 18

Unsigned Division (Paper & Pencil) 100112 = 19 Divisor 10112 Dividend = Quotient × Divisor + Remainder 217 = 19 × 11 + 8 110110012 = 217 -1011 10 10100 -1011 10011 -1011 10002 = 8 Integer Multiplication and Division ICS 233 – KFUPM Quotient Dividend Try to see how big a number can be subtracted, creating a digit of the quotient on each attempt Binary division is accomplished via shifting and subtraction Remainder © Muhamed Mudawar – slide 19

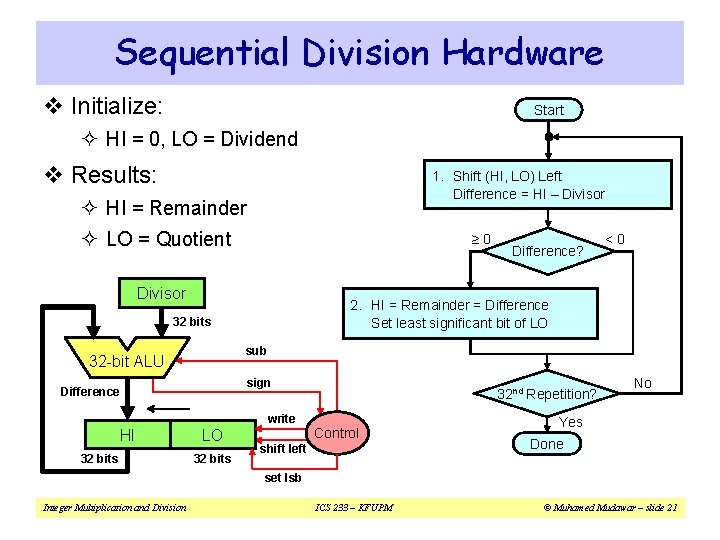
Sequential Division v Uses two registers: HI and LO v Initialize: HI = Remainder = 0 and LO = Dividend v Shift (HI, LO) LEFT by 1 bit (also Shift Quotient LEFT) ² Shift the remainder and dividend registers together LEFT ² Has the same net effect of shifting the divisor RIGHT v Compute: Difference = Remainder – Divisor v If (Difference ≥ 0) then ² Remainder = Difference ² Set Least significant Bit of Quotient v Observation to Reduce Hardware: ² LO register can be also used to store the computed Quotient Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 20

Sequential Division Hardware v Initialize: Start ² HI = 0, LO = Dividend v Results: 1. Shift (HI, LO) Left Difference = HI – Divisor ² HI = Remainder ² LO = Quotient ≥ 0 Divisor sub 32 -bit ALU sign Difference write 32 bits <0 2. HI = Remainder = Difference Set least significant bit of LO 32 bits HI Difference? LO 32 bits 32 nd Repetition? Control shift left No Yes Done set lsb Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 21

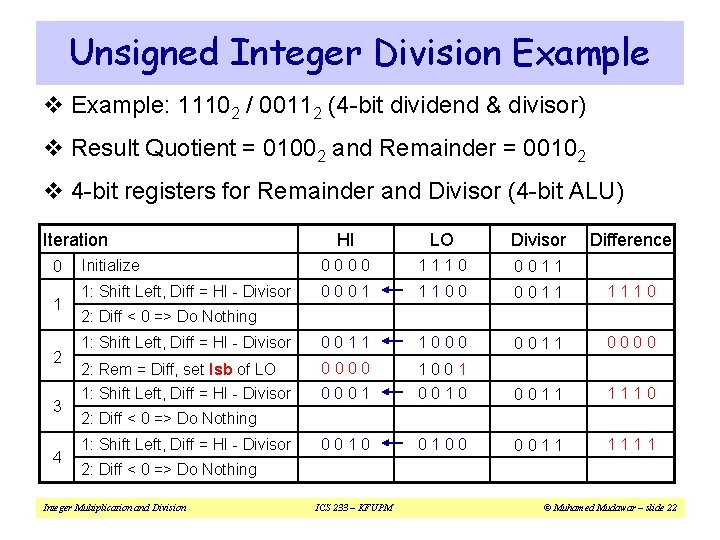
Unsigned Integer Division Example v Example: 11102 / 00112 (4 -bit dividend & divisor) v Result Quotient = 01002 and Remainder = 00102 v 4 -bit registers for Remainder and Divisor (4 -bit ALU) Iteration 0 1 2 3 4 HI LO Divisor Difference Initialize 0000 1110 0011 1: Shift Left, Diff = HI - Divisor 0001 1100 0011 1110 1: Shift Left, Diff = HI - Divisor 0011 1000 0011 0000 2: Rem = Diff, set lsb of LO 1: Shift Left, Diff = HI - Divisor 0000 0001 1001 0010 0011 1110 0010 0100 0011 1111 2: Diff < 0 => Do Nothing 1: Shift Left, Diff = HI - Divisor 2: Diff < 0 => Do Nothing Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 22

Signed Integer Division v Simplest way is to remember the signs v Convert the dividend and divisor to positive ² Obtain the 2's complement if they are negative v Do the unsigned division v Compute the signs of the quotient and remainder ² Quotient sign = Dividend sign XOR Divisor sign ² Remainder sign = Dividend sign v Negate the quotient and remainder if their sign is negative ² Obtain the 2's complement to convert them to negative Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 23

Signed Integer Division Examples 1. Positive Dividend and Positive Divisor ² Example: +17 / +3 Quotient = +5 Remainder = +2 2. Positive Dividend and Negative Divisor ² Example: +17 / – 3 Quotient = – 5 Remainder = +2 3. Negative Dividend and Positive Divisor ² Example: – 17 / +3 Quotient = – 5 Remainder = – 2 4. Negative Dividend and Negative Divisor ² Example: – 17 / – 3 Quotient = +5 Remainder = – 2 The following equation must always hold: Dividend = Quotient × Divisor + Remainder Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 24

Next. . . v Unsigned Integer Multiplication v Signed Integer Multiplication v Faster Multiplication v Integer Division v Integer Multiplication and Division in MIPS Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 25

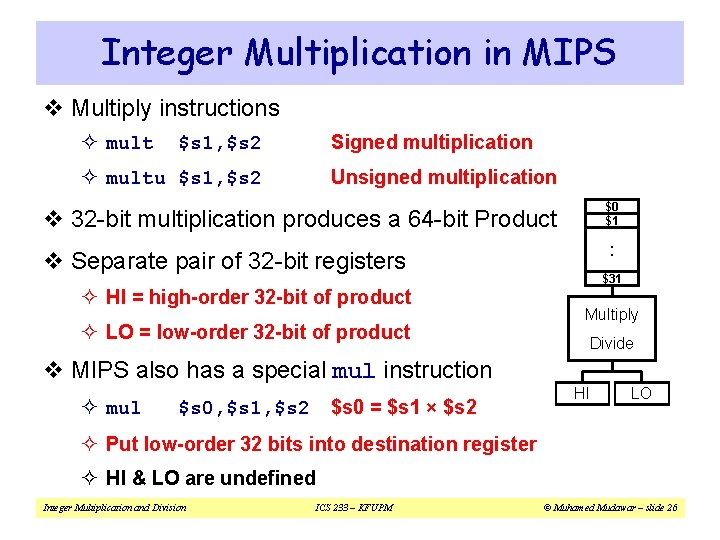
Integer Multiplication in MIPS v Multiply instructions ² mult Signed multiplication $s 1, $s 2 ² multu $s 1, $s 2 Unsigned multiplication $0 $1 v 32 -bit multiplication produces a 64 -bit Product . . v Separate pair of 32 -bit registers ² HI = high-order 32 -bit of product ² LO = low-order 32 -bit of product v MIPS also has a special mul instruction ² mul $s 0 = $s 1 × $s 2 $s 0, $s 1, $s 2 $31 Multiply Divide HI LO ² Put low-order 32 bits into destination register ² HI & LO are undefined Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 26

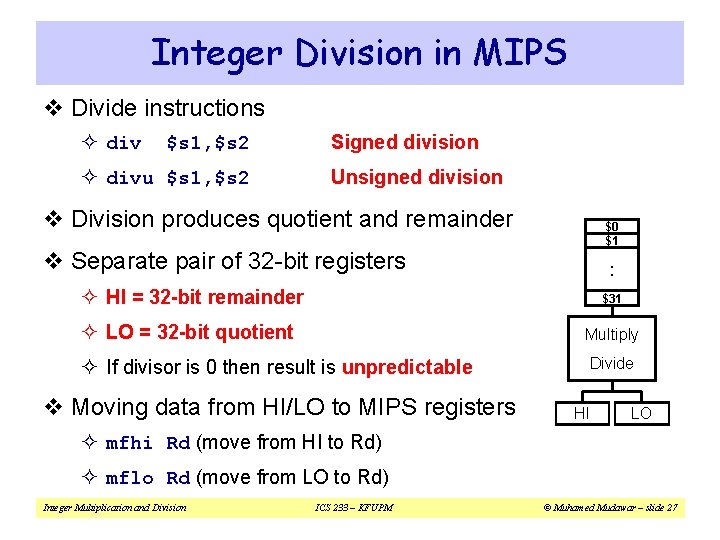
Integer Division in MIPS v Divide instructions ² div $s 1, $s 2 ² divu $s 1, $s 2 Signed division Unsigned division v Division produces quotient and remainder $0 $1 v Separate pair of 32 -bit registers . . ² HI = 32 -bit remainder $31 ² LO = 32 -bit quotient Multiply ² If divisor is 0 then result is unpredictable v Moving data from HI/LO to MIPS registers Divide HI LO ² mfhi Rd (move from HI to Rd) ² mflo Rd (move from LO to Rd) Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 27

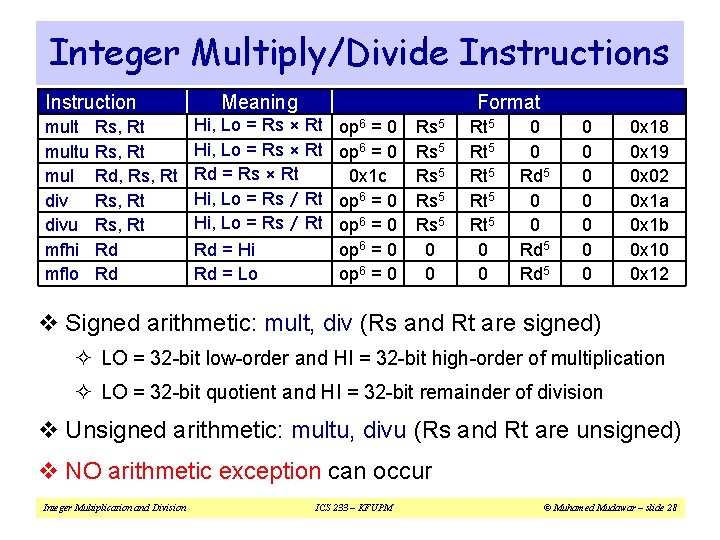
Integer Multiply/Divide Instructions Instruction multu mul divu mfhi mflo Rs, Rt Rd, Rs, Rt Rd Rd Meaning Format Hi, Lo = Rs × Rt Rd = Rs × Rt Hi, Lo = Rs / Rt Rd = Hi Rd = Lo op 6 = 0 0 x 1 c op 6 = 0 Rs 5 Rs 5 0 0 Rt 5 Rt 5 0 0 Rd 5 0 0 0 0 x 18 0 x 19 0 x 02 0 x 1 a 0 x 1 b 0 x 10 0 x 12 v Signed arithmetic: mult, div (Rs and Rt are signed) ² LO = 32 -bit low-order and HI = 32 -bit high-order of multiplication ² LO = 32 -bit quotient and HI = 32 -bit remainder of division v Unsigned arithmetic: multu, divu (Rs and Rt are unsigned) v NO arithmetic exception can occur Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 28

Integer to String Conversion v Objective: convert an unsigned 32 -bit integer to a string v How to obtain the decimal digits of the number? ² Divide the number by 10, Remainder = decimal digit (0 to 9) ² Convert decimal digit into its ASCII representation ('0' to '9') ² Repeat the division until the quotient becomes zero ² Digits are computed backwards from least to most significant v Example: convert 2037 to a string ² Divide 2037/10 quotient = 203 remainder = 7 char = '7' ² Divide 203/10 quotient = 20 remainder = 3 char = '3' ² Divide 20/10 quotient = 2 remainder = 0 char = '0' ² Divide 2/10 quotient = 0 remainder = 2 char = '2' Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 29

Integer to String Procedure #-------------------------------# int 2 str: Converts an unsigned integer into a string # Input: $a 0 = unsigned integer # In/Out: $a 1 = address of string buffer (12 bytes) #-------------------------------int 2 str: move $t 0, $a 0 # $t 0 = dividend = unsigned integer li $t 1, 10 # $t 1 = divisor = 10 addiu $a 1, 11 # start at end of string buffer sb $zero, 0($a 1) # store a NULL byte convert: divu $t 0, $t 1 # LO = quotient, HI = remainder mflo $t 0 # $t 0 = quotient mfhi $t 2 # $t 2 = remainder addiu $t 2, 0 x 30 # convert digit to a character addiu $a 1, -1 # point to previous byte sb $t 2, 0($a 1) # store digit character bnez $t 0, convert # loop if quotient is not 0 jr $ra # return to caller Integer Multiplication and Division ICS 233 – KFUPM © Muhamed Mudawar – slide 30