Integer Multiplication and Division COE 301 Computer Organization

Integer Multiplication and Division COE 301 Computer Organization Prof. Muhamed Mudawar College of Computer Sciences and Engineering King Fahd University of Petroleum and Minerals

Presentation Outline v Unsigned Integer Multiplication v Signed Integer Multiplication v Faster Integer Multiplication v Integer Division v Integer Multiplication and Division in MIPS Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 2

Unsigned Integer Multiplication v Paper and Pencil Example: Multiplicand Multiplier × 11002 = 12 11012 = 13 1100 0000 1100 Product Binary multiplication is easy 0 × multiplicand = 0 1 × multiplicand = multiplicand 100111002 = 156 v n-bit multiplicand × n-bit multiplier = (2 n)-bit product v Accomplished via shifting and addition v Consumes more time and more chip area than addition Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 3

Unsigned Sequential Multiplication v Initialize Product = 0 v Check each bit of the Multiplier v If Multiplier bit = 1 then Product = Product + Multiplicand v Rather than shifting the multiplicand to the left, Shift the Product to the Right Has the same net effect and produces the same result Minimizes the hardware resources v One cycle per iteration (for each bit of the Multiplier) ² Addition and shifting can be done simultaneously Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 4

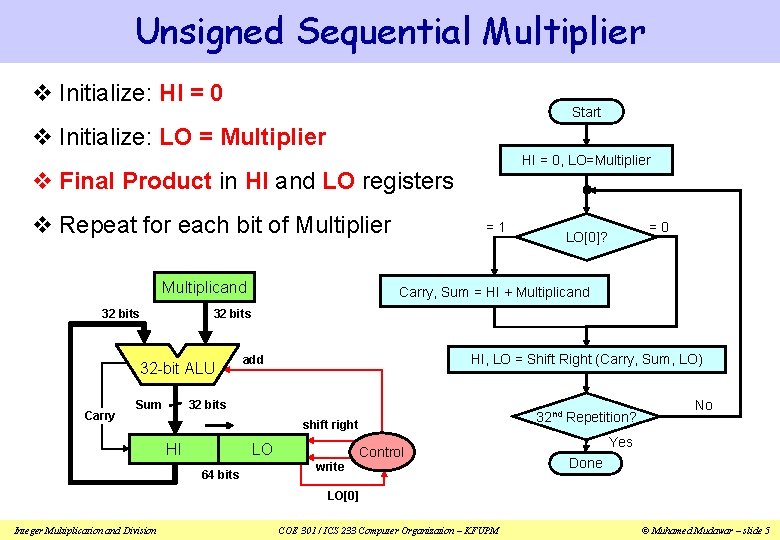
Unsigned Sequential Multiplier v Initialize: HI = 0 Start v Initialize: LO = Multiplier HI = 0, LO=Multiplier v Final Product in HI and LO registers v Repeat for each bit of Multiplier Multiplicand 32 bits =0 LO[0]? Carry, Sum = HI + Multiplicand 32 bits 32 -bit ALU Carry =1 Sum HI, LO = Shift Right (Carry, Sum, LO) add 32 bits 32 nd Repetition? shift right HI LO 64 bits Control write No Yes Done LO[0] Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 5

Sequential Multiplier Example v Consider: 11002 × 11012 , Product = 100111002 v 4 -bit multiplicand multiplier are used in this example v 4 -bit adder produces a 4 -bit Sum + Carry bit Iteration 0 1 2 3 4 Multiplicand Initialize (HI = 0, LO = Multiplier) Product = HI, LO 0000 1101 1100 + LO[0] = 1 => ADD Shift Right (Carry, Sum, LO) by 1 bit Carry 0 1101 1100 0110 1100 0011 LO[0] = 0 => NO addition Shift Right (HI, LO) by 1 bit LO[0] = 1 => ADD + Shift Right (Carry, Sum, LO) by 1 bit Integer Multiplication and Division 1111 0011 0111 1001 1100 + LO[0] = 1 => ADD Shift Right (Carry, Sum, LO) by 1 bit 0 1100 COE 301 / ICS 233 Computer Organization – KFUPM 1 0011 1001 1100 © Muhamed Mudawar – slide 6

Next. . . v Unsigned Integer Multiplication v Signed Integer Multiplication v Faster Integer Multiplication v Integer Division v Integer Multiplication and Division in MIPS Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 7

Signed Integer Multiplication v First attempt: ² Convert multiplier and multiplicand into positive numbers § If negative then obtain the 2's complement and remember the sign ² Perform unsigned multiplication ² Compute the sign of the product ² If product sign < 0 then obtain the 2's complement of the product ² Drawback: additional steps to compute the 2's complement v Better version: ² Use the unsigned multiplication hardware ² When shifting right, extend the sign of the product ² If multiplier is negative, the last step should be a subtract Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 8

Signed Multiplication (Paper & Pencil) v Case 1: Positive Multiplier Multiplicand Multiplier Sign-extension Product × 11002 = -4 01012 = +5 11111100 111011002 = -20 v Case 2: Negative Multiplier Multiplicand Multiplier Sign-extension Product Integer Multiplication and Division × 11002 = -4 11012 = -3 11111100 00100 (2's complement of 1100) 000011002 = +12 COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 9

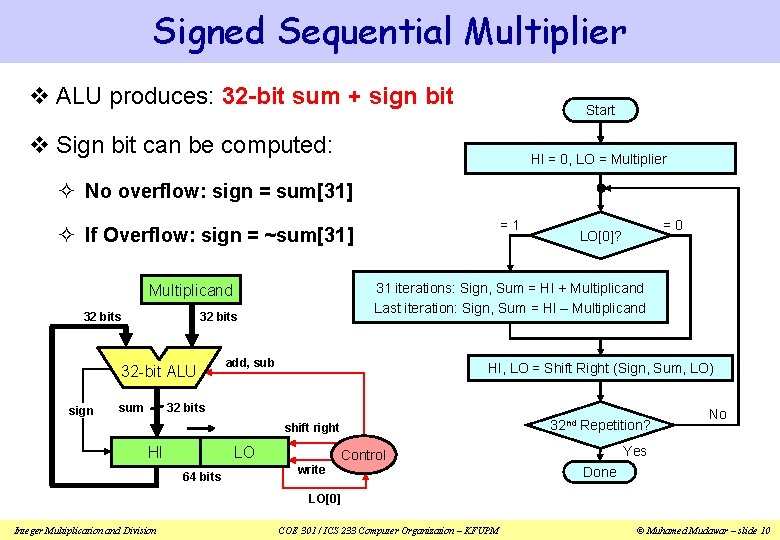
Signed Sequential Multiplier v ALU produces: 32 -bit sum + sign bit Start v Sign bit can be computed: HI = 0, LO = Multiplier ² No overflow: sign = sum[31] =1 ² If Overflow: sign = ~sum[31] 31 iterations: Sign, Sum = HI + Multiplicand Last iteration: Sign, Sum = HI – Multiplicand 32 bits 32 -bit ALU sign sum =0 LO[0]? add, sub HI, LO = Shift Right (Sign, Sum, LO) 32 bits 32 nd Repetition? shift right HI LO 64 bits Yes Control write No Done LO[0] Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 10

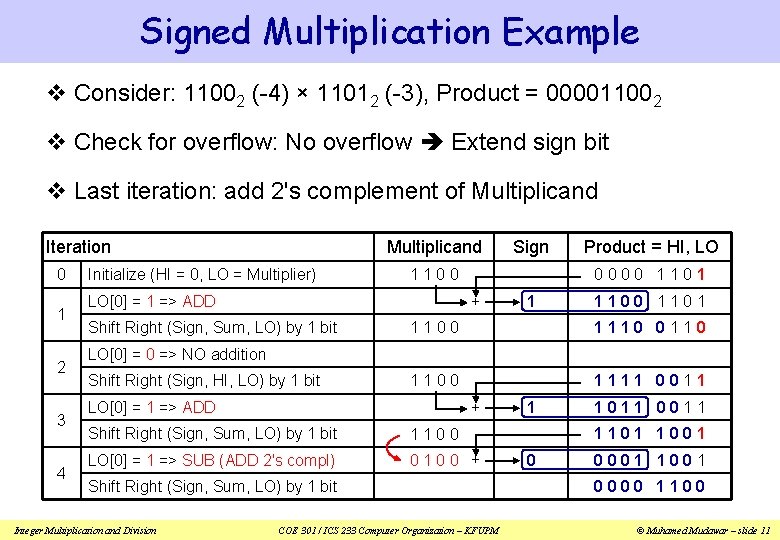
Signed Multiplication Example v Consider: 11002 (-4) × 11012 (-3), Product = 000011002 v Check for overflow: No overflow Extend sign bit v Last iteration: add 2's complement of Multiplicand Iteration 0 1 2 3 4 Multiplicand Initialize (HI = 0, LO = Multiplier) Product = HI, LO 0000 1101 1100 + LO[0] = 1 => ADD Shift Right (Sign, Sum, LO) by 1 bit Sign 1 1100 1101 1100 1110 0110 1100 1111 0011 LO[0] = 0 => NO addition Shift Right (Sign, HI, LO) by 1 bit LO[0] = 1 => ADD + Shift Right (Sign, Sum, LO) by 1 bit 1100 LO[0] = 1 => SUB (ADD 2's compl) 0100 + Shift Right (Sign, Sum, LO) by 1 bit Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM 1 1011 0011 1101 1001 0 0001 1001 0000 1100 © Muhamed Mudawar – slide 11

Next. . . v Unsigned Integer Multiplication v Signed Integer Multiplication v Faster Integer Multiplication v Integer Division v Integer Multiplication and Division in MIPS Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 12

Faster Multiplier v Suppose we want to multiply two numbers A and B ² Example on 4 -bit numbers: A = a 3 a 2 a 1 a 0 and B = b 3 b 2 b 1 b 0 v Step 1: AND (multiply) each bit of A with each bit of B ² Requires n 2 AND gates and produces n 2 product bits ² Position of aibj = (i+j). For example, Position of a 2 b 3 = 2+3 = 5 A×B a 3 b 3 Integer Multiplication and Division a 3 b 0 a 2 b 0 a 1 b 0 a 3 b 1 a 2 b 1 a 1 b 1 a 0 b 1 a 3 b 2 a 2 b 2 a 1 b 2 a 0 b 2 a 2 b 3 a 1 b 3 a 0 b 3 COE 301 / ICS 233 Computer Organization – KFUPM a 0 b 0 © Muhamed Mudawar – slide 13

Adding the Partial Products v Step 2: Add the partial products ² The partial products are shifted and added to compute the product P ² The partial products can be added in parallel ² Different implementations are possible A 3 × B 3 4 -bit Multiplicand 4 -bit Multiplier Partial Products are shifted and added 8 -bit Product P 7 Integer Multiplication and Division Can be added A 3 B 0 in parallel A 3 B 1 A 2 B 1 A 3 B 3 A 3 B 2 A 2 B 3 A 2 B 2 A 1 B 3 A 2 B 0 A 1 B 1 A 1 B 2 A 0 B 3 P 6 P 5 P 4 P 3 COE 301 / ICS 233 Computer Organization – KFUPM A 2 B 2 A 1 B 1 A 0 B 0 A 1 B 0 A 0 B 1 A 0 B 2 A 0 B 0 P 2 P 1 P 0 © Muhamed Mudawar – slide 14

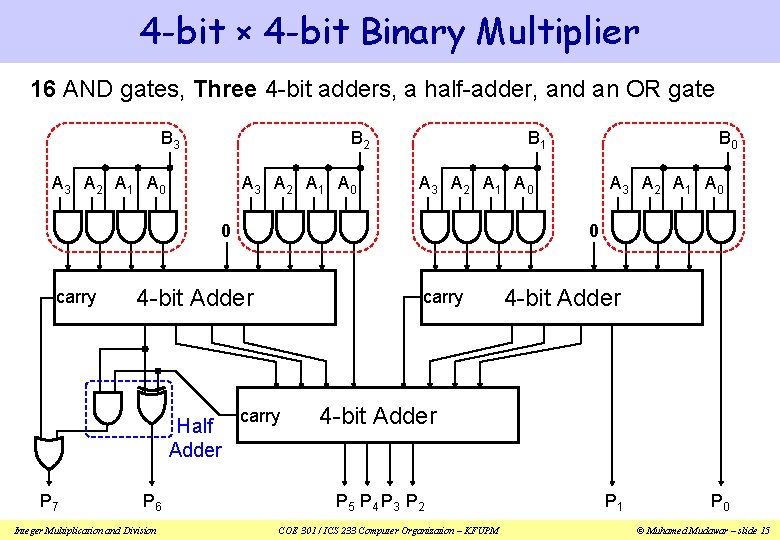
4 -bit × 4 -bit Binary Multiplier 16 AND gates, Three 4 -bit adders, a half-adder, and an OR gate B 3 B 2 A 3 A 2 A 1 A 0 B 1 0 4 -bit Adder Half Adder P 7 P 6 Integer Multiplication and Division A 3 A 2 A 1 A 0 0 carry B 0 carry 4 -bit Adder P 5 P 4 P 3 P 2 COE 301 / ICS 233 Computer Organization – KFUPM P 1 P 0 © Muhamed Mudawar – slide 15

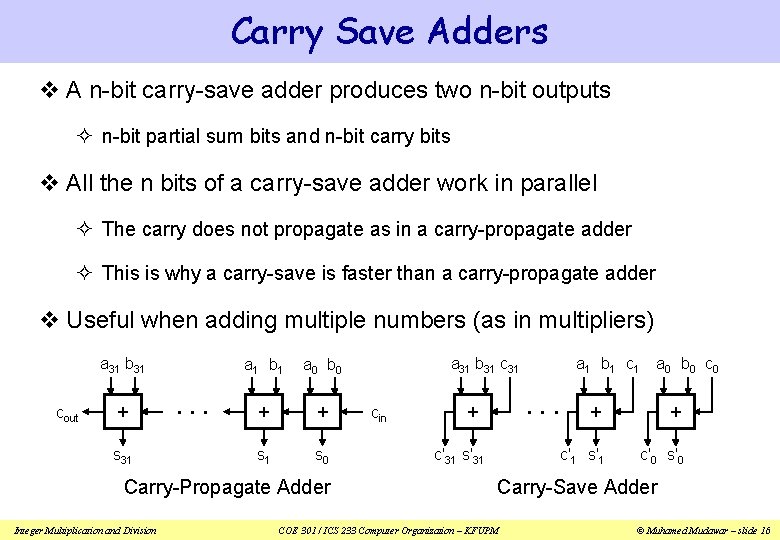
Carry Save Adders v A n-bit carry-save adder produces two n-bit outputs ² n-bit partial sum bits and n-bit carry bits v All the n bits of a carry-save adder work in parallel ² The carry does not propagate as in a carry-propagate adder ² This is why a carry-save is faster than a carry-propagate adder v Useful when adding multiple numbers (as in multipliers) a 31 b 31 cout + s 31 . . . a 1 b 1 a 0 b 0 + + s 1 s 0 Carry-Propagate Adder Integer Multiplication and Division a 31 b 31 cin a 1 b 1 c 1 . . . + c'31 s'31 a 0 b 0 c 0 + + c'1 s'1 c'0 s'0 Carry-Save Adder COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 16

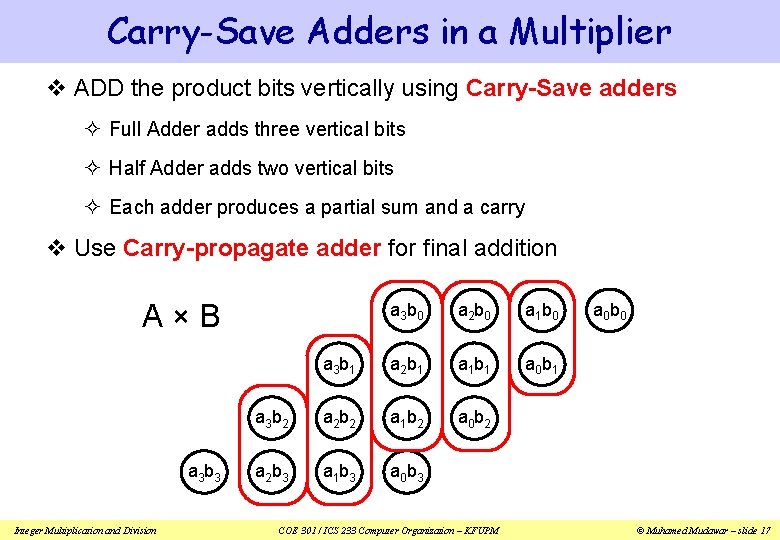
Carry-Save Adders in a Multiplier v ADD the product bits vertically using Carry-Save adders ² Full Adder adds three vertical bits ² Half Adder adds two vertical bits ² Each adder produces a partial sum and a carry v Use Carry-propagate adder for final addition A×B a 3 b 3 Integer Multiplication and Division a 3 b 0 a 2 b 0 a 1 b 0 a 3 b 1 a 2 b 1 a 1 b 1 a 0 b 1 a 3 b 2 a 2 b 2 a 1 b 2 a 0 b 2 a 2 b 3 a 1 b 3 a 0 b 3 COE 301 / ICS 233 Computer Organization – KFUPM a 0 b 0 © Muhamed Mudawar – slide 17

Carry-Save Adders in a Multiplier Step 1: Use carry save adders to add the partial products ² Reduce the partial products to just two numbers Step 2: Use carry-propagate adder to add last two numbers a 3 b 1 a 2 b 2 a 3 b 0 a 2 b 1 a 1 b 3 FA a 2 b 0 a 1 b 1 a 1 b 2 FA a 1 b 0 a 0 b 1 a 0 b 0 a 0 b 2 FA HA Carry Save a 3 b 2 a 2 b 3 a 0 b 3 FA HA FA FA HA P 6 P 5 P 4 P 3 HA Carry Save Adder a 3 b 3 P 7 Integer Multiplication and Division Carry Propagate Adder P 2 COE 301 / ICS 233 Computer Organization – KFUPM P 1 P 0 © Muhamed Mudawar – slide 18

Summary of a Fast Multiplier v A fast n-bit × n-bit multiplier requires: ² n 2 AND gates to produce n 2 product bits in parallel ² Many adders to perform additions in parallel v Uses carry-save adders to reduce delays v Higher cost (more chip area) than sequential multiplier v Higher performance (faster) than sequential multiplier Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 19

Next. . . v Unsigned Integer Multiplication v Signed Integer Multiplication v Faster Integer Multiplication v Integer Division v Integer Multiplication and Division in MIPS Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 20

Unsigned Division (Paper & Pencil) Quotient 100112 = 19 Divisor 10112 Dividend = Quotient × Divisor + Remainder 217 = 19 × 11 + 8 110110012 = 217 -1011 10 10100 -1011 10011 -1011 Check how big a number can be subtracted, creating a bit of the quotient on each attempt Binary division is done via shifting and subtraction 10002 = 8 Integer Multiplication and Division Dividend COE 301 / ICS 233 Computer Organization – KFUPM Remainder © Muhamed Mudawar – slide 21

Sequential Division v Uses two registers: HI and LO v Initialize: HI = Remainder = 0 and LO = Dividend v Shift (HI, LO) LEFT by 1 bit (also Shift Quotient LEFT) ² Shift the remainder and dividend registers together LEFT ² Has the same net effect of shifting the divisor RIGHT v Compute: Difference = Remainder – Divisor v If (Difference ≥ 0) then ² Remainder = Difference ² Set Least significant Bit of Quotient v Observation to Reduce Hardware: ² LO register can be also used to store the computed Quotient Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 22

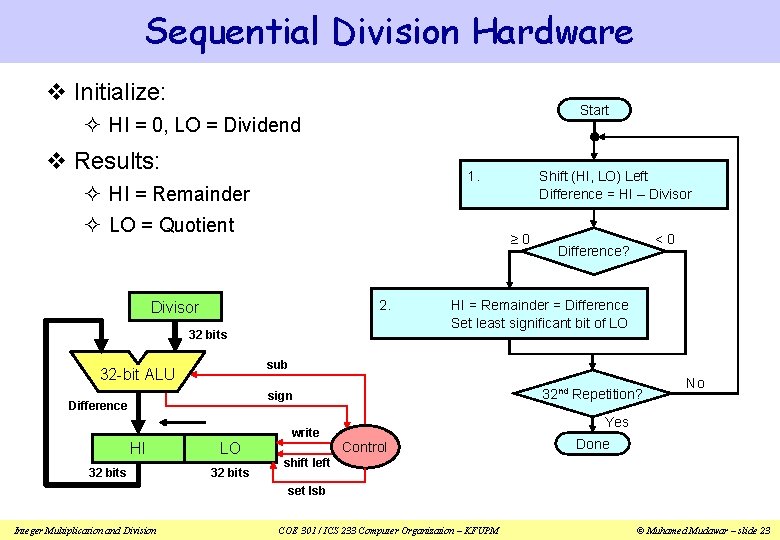
Sequential Division Hardware v Initialize: Start ² HI = 0, LO = Dividend v Results: 1. ² HI = Remainder ² LO = Quotient ≥ 0 2. Divisor 32 bits HI = Remainder = Difference Set least significant bit of LO 32 nd Repetition? sign Difference write 32 bits <0 Difference? sub 32 -bit ALU HI Shift (HI, LO) Left Difference = HI – Divisor LO 32 bits No Yes Control Done shift left set lsb Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 23

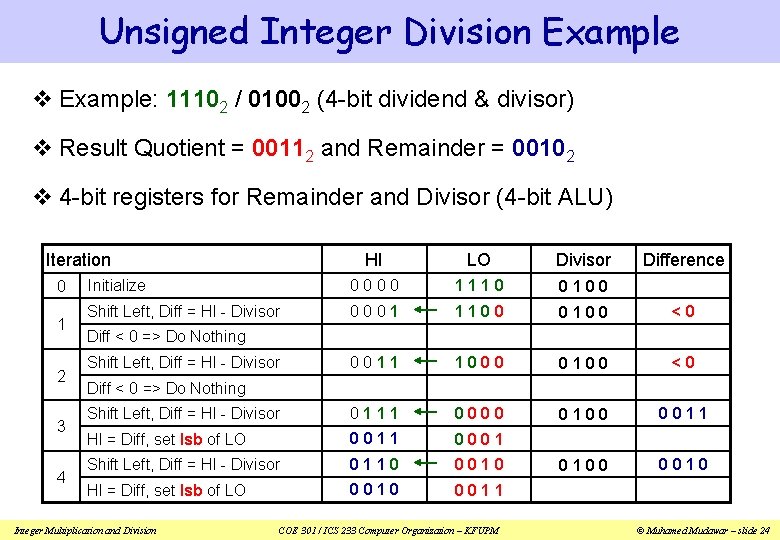
Unsigned Integer Division Example v Example: 11102 / 01002 (4 -bit dividend & divisor) v Result Quotient = 00112 and Remainder = 00102 v 4 -bit registers for Remainder and Divisor (4 -bit ALU) Iteration 0 1 2 3 4 HI LO Divisor Difference Initialize 0000 1110 0100 Shift Left, Diff = HI - Divisor 0001 1100 0100 <0 0011 1000 0100 <0 Shift Left, Diff = HI - Divisor 0111 0000 0100 0011 HI = Diff, set lsb of LO 0011 0001 Shift Left, Diff = HI - Divisor 0110 0010 0100 0010 HI = Diff, set lsb of LO 0010 0011 Diff < 0 => Do Nothing Shift Left, Diff = HI - Divisor Diff < 0 => Do Nothing Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 24

Signed Integer Division v Simplest way is to remember the signs v Convert the dividend and divisor to positive ² Obtain the 2's complement if they are negative v Do the unsigned division v Compute the signs of the quotient and remainder ² Quotient sign = Dividend sign XOR Divisor sign ² Remainder sign = Dividend sign v Negate the quotient and remainder if their sign is negative ² Obtain the 2's complement to convert them to negative Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 25

Signed Integer Division Examples 1. Positive Dividend and Positive Divisor ² Example: +17 / +3 Quotient = +5 Remainder = +2 2. Positive Dividend and Negative Divisor ² Example: +17 / – 3 Quotient = – 5 Remainder = +2 3. Negative Dividend and Positive Divisor ² Example: – 17 / +3 Quotient = – 5 Remainder = – 2 4. Negative Dividend and Negative Divisor ² Example: – 17 / – 3 Quotient = +5 Remainder = – 2 The following equation must always hold: Dividend = Quotient × Divisor + Remainder Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 26

Next. . . v Unsigned Integer Multiplication v Signed Integer Multiplication v Faster Integer Multiplication v Integer Division v Integer Multiplication and Division in MIPS Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 27

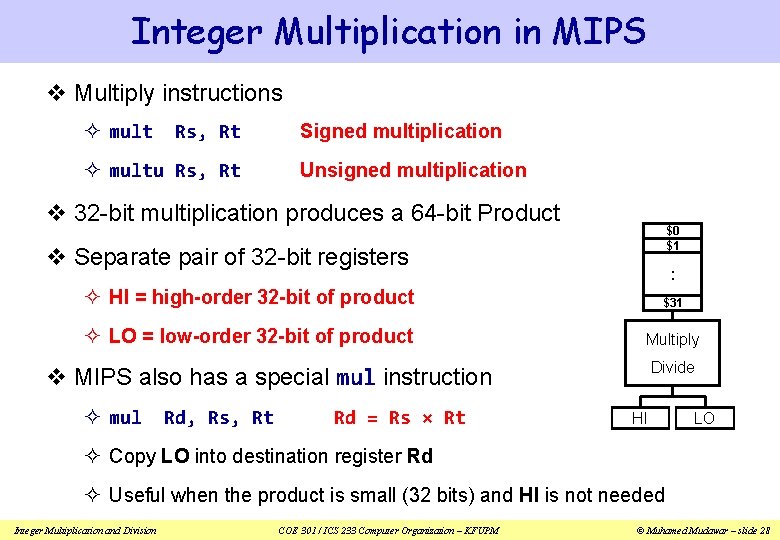
Integer Multiplication in MIPS v Multiply instructions ² mult Rs, Rt ² multu Rs, Rt Signed multiplication Unsigned multiplication v 32 -bit multiplication produces a 64 -bit Product $0 $1 v Separate pair of 32 -bit registers . . ² HI = high-order 32 -bit of product $31 ² LO = low-order 32 -bit of product Multiply Divide v MIPS also has a special mul instruction ² mul Rd, Rs, Rt Rd = Rs × Rt HI LO ² Copy LO into destination register Rd ² Useful when the product is small (32 bits) and HI is not needed Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 28

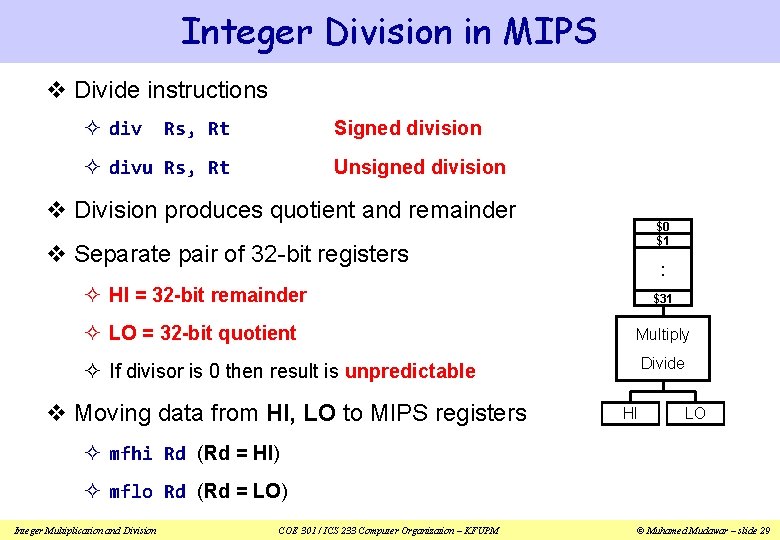
Integer Division in MIPS v Divide instructions ² div Rs, Rt Signed division ² divu Rs, Rt Unsigned division v Division produces quotient and remainder $0 $1 v Separate pair of 32 -bit registers . . ² HI = 32 -bit remainder ² LO = 32 -bit quotient $31 Multiply Divide ² If divisor is 0 then result is unpredictable v Moving data from HI, LO to MIPS registers HI LO ² mfhi Rd (Rd = HI) ² mflo Rd (Rd = LO) Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 29

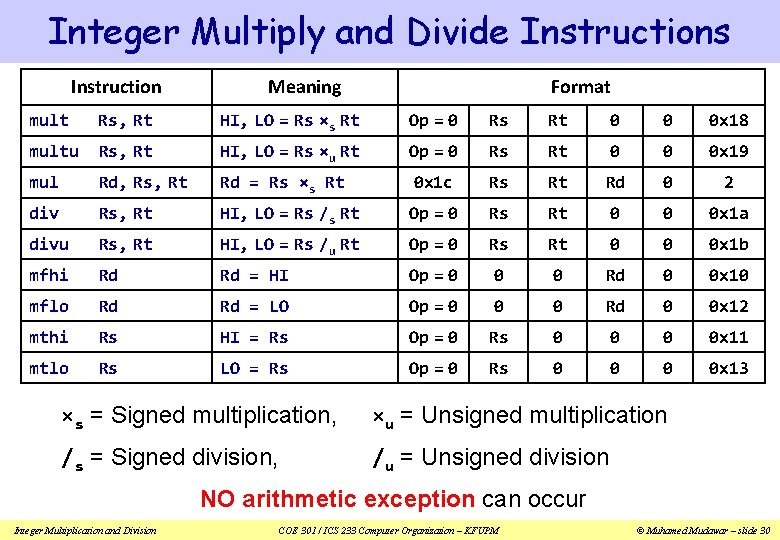
Integer Multiply and Divide Instructions Instruction Meaning Format mult Rs, Rt HI, LO = Rs ×s Rt Op = 0 Rs Rt 0 0 0 x 18 multu Rs, Rt HI, LO = Rs ×u Rt Op = 0 Rs Rt 0 0 0 x 19 mul Rd, Rs, Rt Rd = Rs ×s Rt 0 x 1 c Rs Rt Rd 0 2 div Rs, Rt HI, LO = Rs /s Rt Op = 0 Rs Rt 0 0 0 x 1 a divu Rs, Rt HI, LO = Rs /u Rt Op = 0 Rs Rt 0 0 0 x 1 b mfhi Rd Rd = HI Op = 0 0 0 Rd 0 0 x 10 mflo Rd Rd = LO Op = 0 0 0 Rd 0 0 x 12 mthi Rs HI = Rs Op = 0 Rs 0 0 x 11 mtlo Rs LO = Rs Op = 0 Rs 0 0 x 13 ×s = Signed multiplication, ×u = Unsigned multiplication /s = Signed division, /u = Unsigned division NO arithmetic exception can occur Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 30

String to Integer Conversion v Consider the conversion of string "91052" into an integer '9' '1' '0' '5' '2' v How to convert the string into an integer? v Initialize: sum = 0 v Load each character of the string into a register ² Check if the character is in the range: '0' to '9' ² Convert the character into a digit in the range: 0 to 9 ² Compute: sum = sum * 10 + digit ² Repeat until end of string or a non-digit character is encountered v To convert "91052", initialize sum to 0 then … ² sum = 9, then 910, then 91052 Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 31

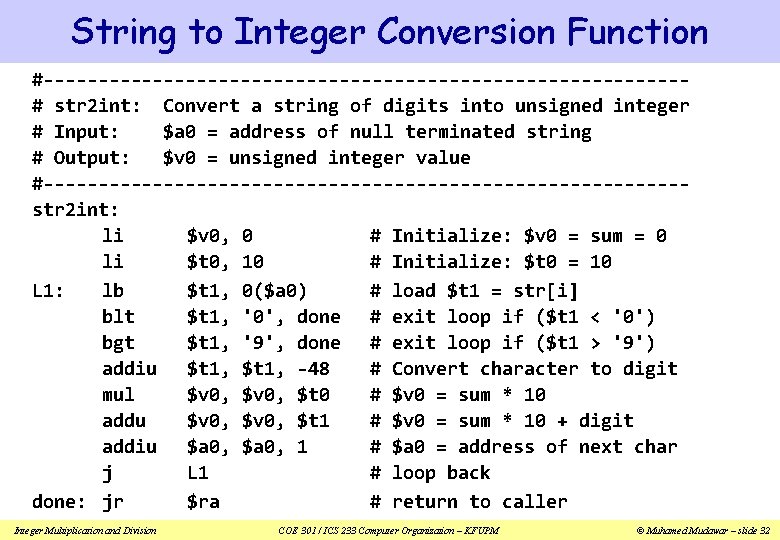
String to Integer Conversion Function #-----------------------------# str 2 int: Convert a string of digits into unsigned integer # Input: $a 0 = address of null terminated string # Output: $v 0 = unsigned integer value #-----------------------------str 2 int: li $v 0, 0 # Initialize: $v 0 = sum = 0 li $t 0, 10 # Initialize: $t 0 = 10 L 1: lb $t 1, 0($a 0) # load $t 1 = str[i] blt $t 1, '0', done # exit loop if ($t 1 < '0') bgt $t 1, '9', done # exit loop if ($t 1 > '9') addiu $t 1, -48 # Convert character to digit mul $v 0, $t 0 # $v 0 = sum * 10 addu $v 0, $t 1 # $v 0 = sum * 10 + digit addiu $a 0, 1 # $a 0 = address of next char j L 1 # loop back done: jr $ra # return to caller Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 32

Integer to String Conversion v Convert an unsigned 32 -bit integer into a string v How to obtain the decimal digits of the number? ² Divide the number by 10, Remainder = decimal digit (0 to 9) ² Convert decimal digit into its ASCII representation ('0' to '9') ² Repeat the division until the quotient becomes zero ² Digits are computed backwards from least to most significant v Example: convert 2037 to a string ² Divide 2037/10 quotient = 203 remainder = 7 char = '7' ² Divide 203/10 quotient = 20 remainder = 3 char = '3' ² Divide 20/10 quotient = 2 remainder = 0 char = '0' ² Divide 2/10 quotient = 0 remainder = 2 char = '2' Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 33

Integer to String Conversion Function #-----------------------------# int 2 str: Converts an unsigned integer into a string # Input: $a 0 = value, $a 1 = buffer address (12 bytes) # Output: $v 0 = address of converted string in buffer #-----------------------------int 2 str: li $t 0, 10 # $t 0 = divisor = 10 addiu $v 0, $a 1, 11 # start at end of buffer sb $zero, 0($v 0) # store a NULL character L 2: divu $a 0, $t 0 # LO = value/10, HI = value%10 mflo $a 0 # $a 0 = value/10 mfhi $t 1 # $t 1 = value%10 addiu $t 1, 48 # convert digit into ASCII addiu $v 0, -1 # point to previous byte sb $t 1, 0($v 0) # store character in memory bnez $a 0, L 2 # loop if value is not 0 jr $ra # return to caller Integer Multiplication and Division COE 301 / ICS 233 Computer Organization – KFUPM © Muhamed Mudawar – slide 34