Integer Linear Programming Professor Ahmadi Slide 1 Integer

Integer Linear Programming Professor Ahmadi Slide 1

Integer Linear Programming n n n Types of Integer Linear Programming Models Graphical Solution for an All-Integer LP Spreadsheet Solution for an All-Integer LP Application Involving 0 -l Variables Special 0 -1 Constraints Slide 2

Types of Integer Programming Models n n n A linear program in which all the variables are restricted to be integers is called an integer linear program (ILP). If only a subset of the variables are restricted to be integers, the problem is called a mixed integer linear program (MILP). Binary variables are variables whose values are restricted to be 0 or 1. If all variables are restricted to be 0 or 1, the problem is called a 0 -1 or binary integer program. Slide 3

Example: All-Integer LP n Consider the following all-integer linear program: Max 3 x 1 + 2 x 2 s. t. 3 x 1 + x 2 < 9 x 1 + 3 x 2 < 7 -x 1 + x 2 < 1 x 1, x 2 > 0 and integer Slide 4

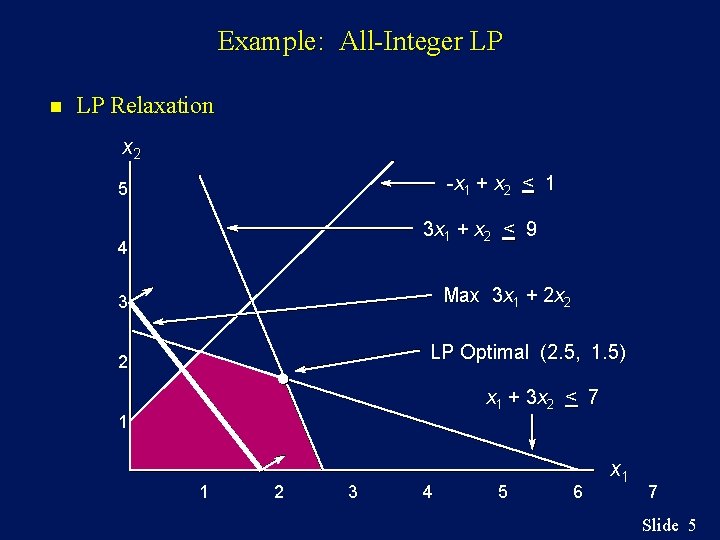
Example: All-Integer LP n LP Relaxation x 2 -x 1 + x 2 < 1 5 3 x 1 + x 2 < 9 4 Max 3 x 1 + 2 x 2 3 LP Optimal (2. 5, 1. 5) 2 x 1 + 3 x 2 < 7 1 1 2 3 4 5 6 x 1 7 Slide 5

Example: All-Integer LP n LP Relaxation Solving the problem as a linear program ignoring the integer constraints, the optimal solution to the linear program gives fractional values for both x 1 and x 2. From the graph on the previous slide, we see that the optimal solution to the linear program is: x 1 = 2. 5, x 2 = 1. 5, z = 10. 5 Slide 6

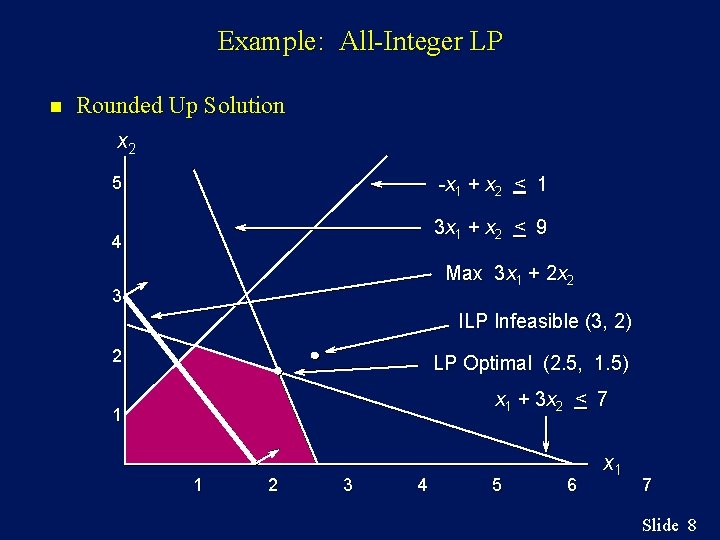
Example: All-Integer LP n Rounding Up If we round up the fractional solution (x 1 = 2. 5, x 2 = 1. 5) to the LP relaxation problem, we get x 1 = 3 and x 2 = 2. From the graph on the next page, we see that this point lies outside the feasible region, making this solution infeasible. Slide 7

Example: All-Integer LP n Rounded Up Solution x 2 -x 1 + x 2 < 1 5 3 x 1 + x 2 < 9 4 Max 3 x 1 + 2 x 2 3 ILP Infeasible (3, 2) 2 LP Optimal (2. 5, 1. 5) x 1 + 3 x 2 < 7 1 1 2 3 4 5 6 x 1 7 Slide 8

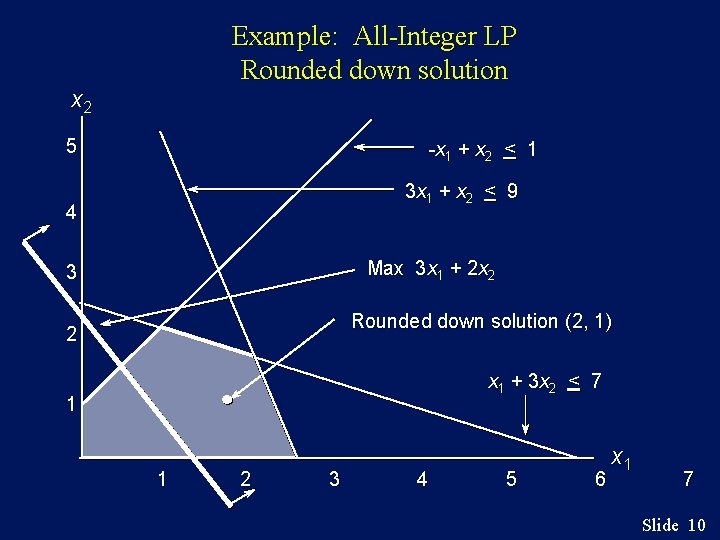
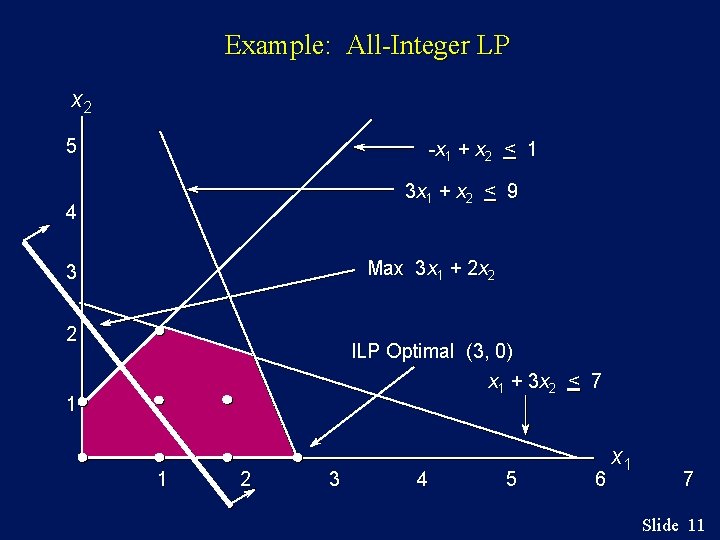
Example: All-Integer LP n Rounding Down By rounding the optimal solution down to x 1 = 2, x 2 = 1, we see that this solution indeed is an integer solution within the feasible region, and substituting in the objective function, it gives z = 8. We have found a feasible all-integer solution, but have we found the optimal all-integer solution? ----------The answer is NO! The optimal solution is x 1 = 3 and x 2 = 0 giving z = 9, as evidenced in the next two slides. Slide 9

Example: All-Integer LP Rounded down solution x 2 5 -x 1 + x 2 < 1 3 x 1 + x 2 < 9 4 Max 3 x 1 + 2 x 2 3 Rounded down solution (2, 1) 2 x 1 + 3 x 2 < 7 1 1 2 3 4 5 6 x 1 7 Slide 10

Example: All-Integer LP x 2 5 -x 1 + x 2 < 1 3 x 1 + x 2 < 9 4 Max 3 x 1 + 2 x 2 3 2 ILP Optimal (3, 0) x 1 + 3 x 2 < 7 1 1 2 3 4 5 6 x 1 7 Slide 11

Example: All-Integer LP n Complete Enumeration of Feasible ILP Solutions There are eight feasible integer solutions to this problem: x 1 x 2 z 1. 0 0 0 2. 1 0 3 3. 2 0 6 4. 3 0 9 optimal solution 5. 0 1 2 6. 1 1 5 7. 2 1 8 8. 1 2 7 Slide 12

Special 0 -1 Constraints n When xi and xj represent binary variables designating whether projects i and j have been completed, the following special constraints may be formulated: • At most k out of n projects will be completed: Sxj < k • Project j is conditional on project i: xj - xi < 0 • Project i is a co-requisite for project j: xj - xi = 0 • Projects i and j are mutually exclusive: xi + xj < 1 Slide 13

Example: Chattanooga Electronics, Inc. is planning to expand its operations into other electronic appliances. The company has identified seven new product lines it can carry. Relevant information about each line follows: Initial Floor Space Exp. Rate Product Line Investment (Sq. Ft. ) of Return 1. Digital TVs $60, 000 125 8. 1% 2. Color TVs 12, 000 150 9. 0 3. Large Screen TVs 20, 000 200 11. 0 4. DVDs 14, 000 40 10. 2 5. DVD/RWs 15, 000 40 10. 5 6. Video Games 2, 000 20 14. 1 7. PC Computers 32, 000 13. 2 Slide 14

Example: Chattanooga Electronics Chattanooga has decided that they should not stock large screen TVs unless they stock either digital or color TVs. Also, they will not stock both types of DVDs, and they will stock video games if they stock color TVs. Finally, the company wishes to introduce at least three new product lines. If the company has $45, 000 to invest and 420 sq. ft. of floor space available, formulate an integer linear program for Chattanooga to maximize its overall expected rate of return. Slide 15

Example: Chattanooga Electronics n n Define the Decision Variables xj = 1 if product line j is introduced; = 0 otherwise. Define the Objective Function Maximize total overall expected return: Max. 081(60000)x 1 +. 09(12000)x 2 +. 11(20000)x 3 +. 102(14000)x 4 +. 105(15000)x 5 +. 141(2000)x 6 +. 132(32000)x 7 or Max 4860 x 1 + 1080 x 2 + 2200 x 3 + 1428 x 4 + 1575 x 5 + 282 x 6 + 4224 x 7 Slide 16

Example: Chattanooga Electronics n Define the Constraints 1) Money: 2) Space: 3) Stock large screen TVs only if stock digital or color: Slide 17

Example: Chattanooga Electronics n Define the Constraints (continued) 4) Do not stock both types of DVDs: 5) Stock video games if they stock color TV's: 6) At least 3 new lines: 7) Variables are 0 or 1: xj = 0 or 1 for j = 1, , , 7 Slide 18

Example: Mo’s Programming Mo's Programming has five idle Programmers and four custom Programs to develop. The estimated time (in hours) it would take each Programmer to write each Program is listed below. (An 'X' in the table indicates an unacceptable Programmer-Program assignment. ) Programmer Program 1 2 3 4 5 Java 19 23 20 21 18 C++ 11 14 X 12 10 Assembler 12 8 11 X 9 Pascal X 20 20 18 21 Slide 19

Example: Mo’s Programming Formulate an integer program for determining the Programmer-Program assignments that minimize the total estimated time spent writing the four Programs. No Programmer is to be assigned more than one Program and each Program is to be worked on by only one Programmer. ----------This problem can be formulated as a 0 -1 integer program. The LP solution to this problem will automatically be integer (0 -1). Slide 20

Example: Mo’s Programming n n Define the decision variables xij = 1 if Program i is assigned to Programmer j = 0 otherwise. Number of decision variables = [(number of Programs)(number of Programmers)] - (number of unacceptable assignments) = [4(5)] - 3 = 17 Define the objective function Minimize total time spent writing Programs: Min 19 x 11 + 23 x 12 + 20 x 13 + 21 x 14 + 18 x 15 + 11 x 21 + 14 x 22 + 12 x 24 + 10 x 25 + 12 x 31 + 8 x 32 + 11 x 33 + 9 x 35 + 20 x 42 + 20 x 43 + 18 x 44 + 21 x 45 Slide 21

Example: Mo’s Programming n Define the Constraints Exactly one Programmer per Program: 1) x 11 + x 12 + x 13 + x 14 + x 15 = 1 2) x 21 + x 22 + x 24 + x 25 = 1 3) x 31 + x 32 + x 33 + x 35 = 1 4) x 42 + x 43 + x 44 + x 45 = 1 Slide 22

Example: Mo’s Programming n Define the Constraints (continued) No more than one Program per Programmer: 5) x 11 + x 21 + x 31 < 1 6) x 21 + x 22 + x 23 + x 24 < 1 7) x 31 + x 33 + x 34 < 1 8) x 41 + x 42 + x 44 < 1 9) x 51 + x 52 + x 53 + x 54 < 1 Non-negativity: xij > 0 for i = 1, . . , 4 and j = 1, . . , 5 Slide 23

The End of Chapter Slide 24