Integer Factorization Various approaches trial divisions up to

Integer Factorization • Various approaches – trial divisions up to B find factors up to B 2 – probabilistic approaches find factors up to B 4 • Pollard’s rho heutistic – neither the running time nor success is guaranteed – any divisor it finds will be correct, but it may never report any results – in practice, it is the most effective means of factorization currently known – it will print the factor p after approximately p iterations; thus it finds small factors quickly

Pollard’s rho heuristic • The while loop searches indefinitely for factors generating a new xi each time • Lines 1 -4 are for initialization • The xi values saved in y are when i = 1, 2, 4, 8, 16, … • d is the gcd of y- xi and n; if it is nontrivial then it is printed as a factor of n • If n is composite, we expect to find enough divisors to factor n after approximately n 1/4 updates • Zn is finite, so we need to estimate how long until the xis repeat themselves

How long until the xis repeat? • An analysis – let p be a nontrivial factor of n so gcd(p, n/p)=1 – the xi induce a sequence xi’ mod p where xi’ = xi mod p – by the Chinese remainder theorem xi+1’ 2 = (xi’ 2 - 1 )mod p since (x mod n)mod p=x mod p – by the birthday-paradox analysis (section 6. 6. 1) we expect repetition in aprx. O( p) – once k becomes large enough we will make a complete cycle around the loop without changing y, then a factor is discovered since xi y (mod p) – the factor will be p or a multiple of p

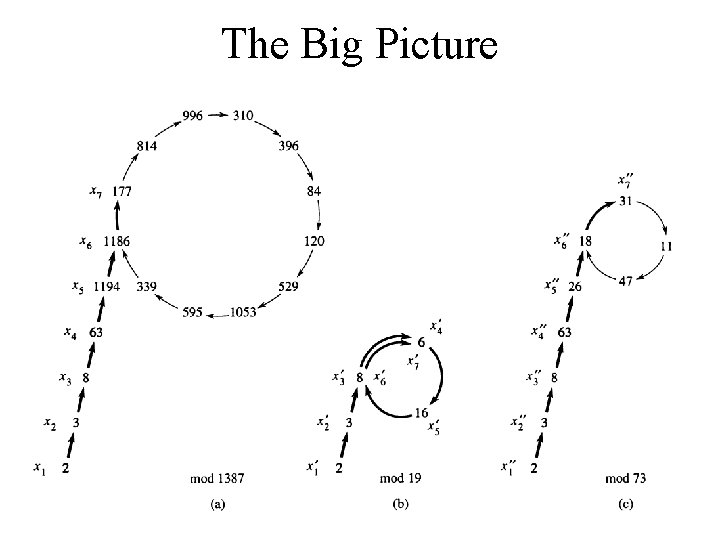
The Big Picture

The rho diagrams • (a) is generated by the xi starting at 2 for n = 1387 • The factor 19 (since 1387 = 19 * 73) is discovered when the xi is 177, this is before the value 1186 is repeated • (b) show the recurrence for mod 19, every xi in part (a) is equivalent to the xi‘ mod 19 • (c) shows the recurrence for mod 73, again every xi in part (a) is equivalent to the xi” mod 73 • By the Chinese remainder theorem, each node in (a) corresponds to a pair of nodes in (b) and (c)