Integer Exponents Day 1 Definitions EXPONENT BASE Base

Integer Exponents Day 1

Definitions EXPONENT BASE Base: The term/variable of which is being raised upon Exponent: The term/variable is raised by a term. AKA Power


Example 1

Example 2 5

Example 3 6

Solve:

Laws of Exponents https: //www. youtube. com/watch? v=QIZTruxt 2 r. Q

Any number raised to the first power is … 31 = 871 = 5289211 = Rule: Any number raised to the first power is itself. (a 1 = a)

Any number raised to the power of zero is ONE! 30 = 870 = 5289210 = Rule: a 0 = 1

Negative Power Property Saying goes: NO NEGATIVE POWERS What are the base(s) and the power(s)?

Negative Power Property
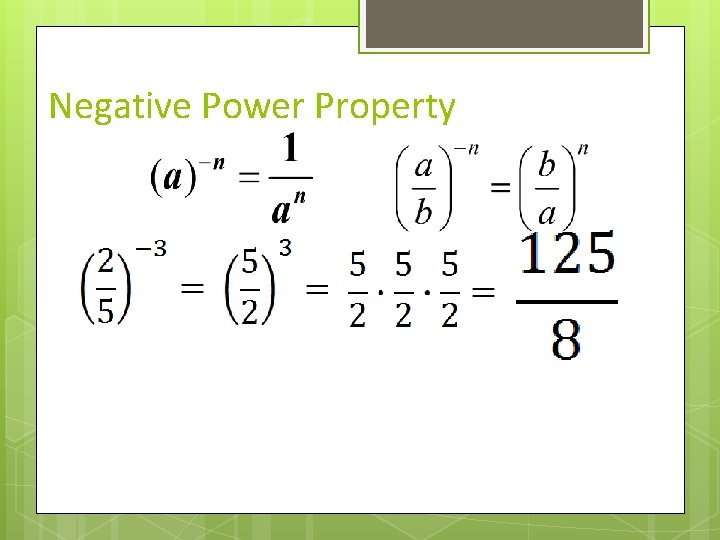
Negative Power Property

Practice 1) 2) 3) 4) 5) (-4)2 73 -54 101 95 6) (-2)0 7) (-2)-1 8) 0 -3 9) 3 -4 10) (¼)0

Product Rule Saying goes: BASE, ADD If the BASES are same, ADD the powers What are the base(s) and the power(s)?

Product of a Power

Product of a Power


Quotient Power Property Saying goes: When dividing an expression with a power, SUBTRACT the powers. They must have the same base in order to subtract. What are the base(s) and the power(s)?

Quotient Power Property

Quotient Power Property
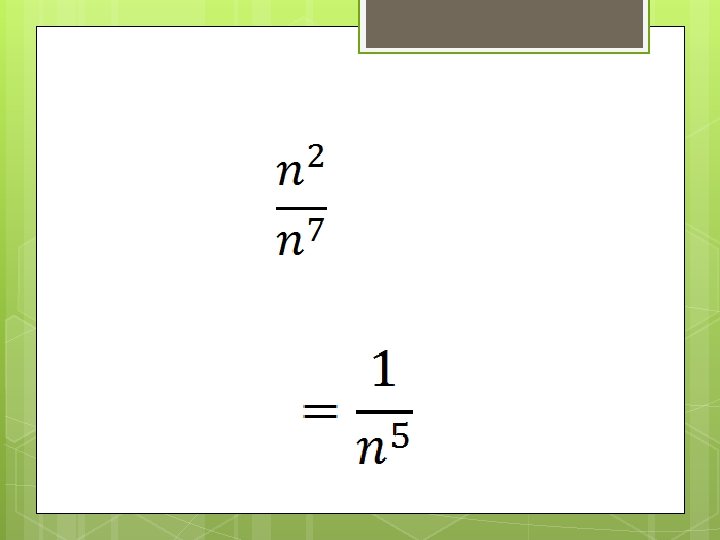

Power of a Power Saying goes: POWER, MULTIPLY If the POWERS are near each other, MULTIPLY the powers – usually deals with PARENTHESES What are the base(s) and the power(s)?

Power of a Power

Power of a Power


Power of a Product Saying goes: BASES DISTRIBUTE THE POWER TO THE What are the base(s) and the power(s)?

Power of a Product How many bases does this problem have?

Properties of Exponents Negative Power Property: Product of a Power: Power of a Power: Quotient Power Property:

Do Now – December 6 th NO CALCULATOR 1. 2. 3. 4. 5. Solve: 0. 2 x = 7 - 0. 8 x 6 -3 -40 (-8)2 -34
- Slides: 30