Instrumental orchestration in Chinese mathematics lessons with dynamic

Instrumental orchestration in Chinese mathematics lessons with dynamic geometry Fangchun Zhu fangchun. zhu@ens-lyon. fr Supervisor: Sophie Soury-Lavergne Binyan Xu

Outlines 1) Context 2) Research questions 3) Instrumental orchestration 4) Types of instrumental orchestration 5) Methods 6) Analysis based on one Chinese mathematics lesson 7) Conclusion 8) Examples of students’ operating dynamic geometry 9) Workshop

Context • There are three important areas in mathematics educational research on technology (Sinclair et al. , 2016): • (1) the introduction and design of new technology, both hardware and software, • (2) theory and methodology for a better understanding of the role of existing and emerging technology, and • (3) empirical studies on the use of technology in teaching and learning. • But how technology affects mathematics teaching and learning, is far from being explained clearly (Bretscher, 2014). • What is difficult for teacher to integrate technology into his or her mathematics teaching? • Lagrange et al (2003) has shown that there are too many variables to manage in the classroom: one of these variables is that teachers need to make transformation between old and new didactical practices (Assude & Gelis, 2002). • In order to help teachers integrate technology into mathematics didactical process, we need to make deep understanding of teachers’ managing mathematics lessons with technological tools. To account for 3 this topic, Trouche (Trouche, 2004) introduces instrumental orchestration to describe this process.

Research question • This study wants to describe teachers’ real practices with dynamic geometry software and give a deep understanding of how mathematics teachers integrate dynamic geometry software in their lessons. 4

Instrumental orchestration • An instrumental orchestration is defined as how teachers want to organize the class teaching with different kinds of artefacts available in learning environment in order to help students learn mathematics (Trouche, 2004). • We can distinguish instrumental orchestration into three different elements: a didactic configuration, an exploitation mode and a didactical performance (Drijvers, Doorman, Boon, Reed, & Gravemeijer, 2010). 5

Instrumental orchestration Didactic An arrangement configuration environment, Focus in this research the The process of teacher’s choice and use of the a mathematical tasks or the geometry software configuration of the teaching setting and the in the classroom and how to configure them in artefacts involved in it. the classroom. Exploitation The way the teacher decides to exploit a The sequence of the tasks teachers showed to mode didactical configuration for the benefit of his the students and the role mathematical or her didactical intentions. software played in the tasks. It is one way of or of artefacts in other in words, decision teacher takes. Didactical The ad hoc decisions taken while teaching The interaction between teachers and performance on how to actually perform in the chosen students: the questions teachers posed, the didactic configuration and exploitation mode. feedback teachers gave and the purpose of each questions. 6

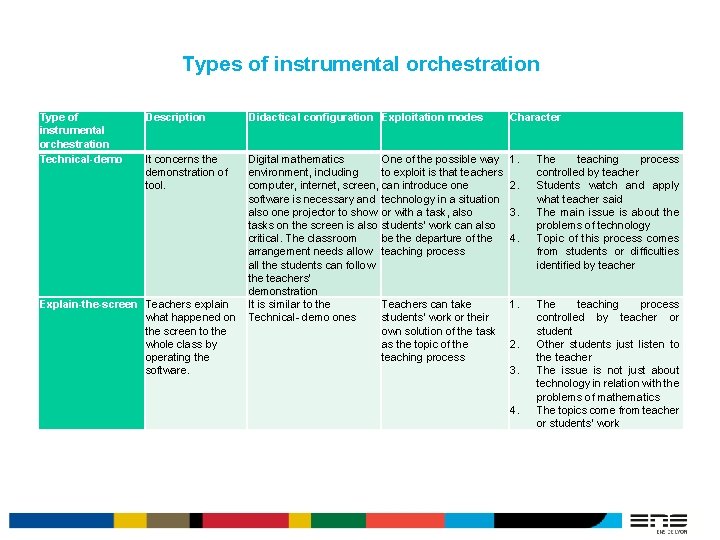
Types of instrumental orchestration Type of instrumental orchestration Technical-demo Description Didactical configuration Exploitation modes Character It concerns the demonstration of tool. Digital mathematics One of the possible way environment, including to exploit is that teachers computer, internet, screen, can introduce one software is necessary and technology in a situation also one projector to show or with a task, also tasks on the screen is also students’ work can also critical. The classroom be the departure of the arrangement needs allow teaching process all the students can follow the teachers’ demonstration It is similar to the Teachers can take Technical- demo ones students’ work or their own solution of the task as the topic of the teaching process 1. Explain-the-screen Teachers explain what happened on the screen to the whole class by operating the software. 2. 3. 4. 1. 2. 3. 4. 7 The teaching process controlled by teacher Students watch and apply what teacher said The main issue is about the problems of technology Topic of this process comes from students or difficulties identified by teacher The teaching process controlled by teacher or student Other students just listen to the teacher The issue is not just about technology in relation with the problems of mathematics The topics come from teacher or students’ work

Types of instrumental orchestration Type of Description Didactical instrumental configuration orchestration Guide-and-explain Students begin to Similar to explain-theexplain the mathematics screen contents shown on the screen guided by the questions posed by teachers Link-screen-board This type begins to concern the relationship between two main resources in classroom: screen and board. Teachers begin to think how to represent what happens in the technological environment only with paper, book and blackboard Exploitation modes Character Teachers can take 1. students’ work or their own solution of the 2. task as the topic of the 3. teaching process and pose questions while teaching 4. The configuration is Similar to “explain-the- 1. also similar to the screen”, students’ work above two types, digital or teachers’ own 2. mathematics solution to a task can environment with a be the departure of the 3. projector is critical. In teaching process this type, some traditional resource like blackboard is needed also. And we need to let both blackboard and 4. screen are visible to the students. 8 The teaching process controlled by teacher Students answer questions The issue is not just about technology in relation with the problems of mathematics The topics come from teacher or students’ work The teaching process controlled by teachers Students just listen to the teacher use more than one resources in class such as technology, board, chalk and so on, issues related to the two types of representations The topic comes from students’ work or a task

Types of instrumental orchestration Type of instrumental Description orchestration Discuss-the-screen Students participate into the discussion. Teachers may just help or talk with the students if they need help. Spot-and-show Didactical configuration Exploitation modes Character Digital mathematics Students’ work, a 1. environment and projector task, or a problem or which can show tasks or approach set by the students’ work are teacher can be the necessary. And the topic of discussion 2. classroom arrangement need to make students 3. discuss easily 4. one or more students Including digital explain their work to the mathematics environment whole class and others or teacher give some feedback or ask some questions. Teachers choose 1. some students whose work are shown on the screen to explain 2. their solutions, other students or 3. themselves give some feedbacks 4. 9 Students began to participate in the process; teachers are not the center of the class Teacher or other students give feedbacks The topic is about mathematics The issue comes from students’ work or a task Students themselves make the explanations not the teacher Teacher and other students give feedback The topic is about mathematics Students’ work was shown on the screen as a topic of the following class

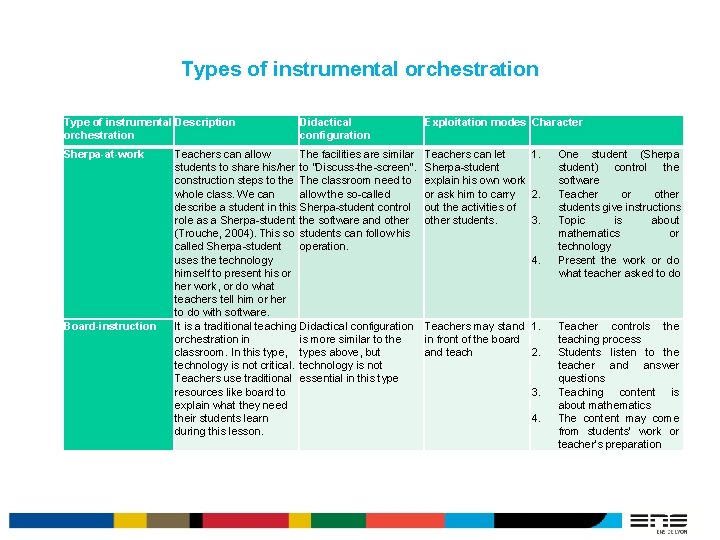
Types of instrumental orchestration Type of instrumental Description orchestration Didactical configuration Exploitation modes Character Sherpa-at-work The facilities are similar to “Discuss-the-screen”. The classroom need to allow the so-called Sherpa-student control the software and other students can follow his operation. Teachers can let 1. Sherpa-student explain his own work or ask him to carry 2. out the activities of other students. 3. Board-instruction Teachers can allow students to share his/her construction steps to the whole class. We can describe a student in this role as a Sherpa-student (Trouche, 2004). This so called Sherpa-student uses the technology himself to present his or her work, or do what teachers tell him or her to do with software. It is a traditional teaching orchestration in classroom. In this type, technology is not critical. Teachers use traditional resources like board to explain what they need their students learn during this lesson. 4. Didactical configuration is more similar to the types above, but technology is not essential in this type Teachers may stand 1. in front of the board and teach 2. 3. 4. 10 One student (Sherpa student) control the software Teacher or other students give instructions Topic is about mathematics or technology Present the work or do what teacher asked to do Teacher controls the teaching process Students listen to the teacher and answer questions Teaching content is about mathematics The content may come from students’ work or teacher’s preparation

Method • Lessons observed in this research • Two lessons were analyzed based on the framework of instrumental orchestration. • Teacher included in this research • Teacher: ZH (pseudonym) who have about 20 years of teaching experiences and is very familiar with using dynamic geometry software in mathematics teaching. 11

Tasks in China Task Description ZH designed one diagram of triangle whose length of side AC and BC is determined (AC = 4, BC = 6). Point A could be moved while points B and C were stable. From the diagram, the trace of point A is like a circle. The first task contained one moving point P. At first, point P is coincide with point A then it moves from A to B to C to D. Students need to find out the mathematical relation between the area of triangle APD and the length of moving trace. The second task contained two moving points, point A and C, but these points do not move according to line but like a circle. There is a right triangle ABC, ∠C=90°, BC=4, AC=3. ZH makes triangle ABC turns around point B to make point A on the line BC (point A’), students need to find the length of segment AA’ The third task, ZH designed one rectangle ABCD. There is a point E which moves along segment BC, from point B to C. Point B’ is a symmetry point of point B according to segment AE like the figure shown. Students need to find what kind of trace point B’ moves when point E is moving along BC 12

Results: type of instrumental orchestration in China Type of instrumental First lesson orchestration Duration Second lesson Duration Technical-demo Explain-the-screen 5 7 minutes 7 8 minutes Guide-and-explain 3 11 minutes 3 5 minutes Link-screen-board 1 30 seconds Discuss-the-screen 2 2 minutes 2 5 minutes 1 2 minutes Spot-and-show Sherpa-at-work Board-instruction 1 5 minutes 13

Example episodes Discuss-the-screen • All the students in this lesson were divided into small groups (two or three students) • ZH shown the task and diagram students need to discuss and let the diagram move automatically. • The discussion process was not controlled by ZH, he just decided the questions to talk about and the total time of discussion. • The topic of this discussion is a mathematics task prepared by ZH before the lesson. • ZH walked around and listened the students’ talking. • There is no interaction between ZH and his students. • Dynamic geometry software played as a projector to show the task, • Students did not operate software any more. 14

Example episodes Explain-the-screen and guide-and-explain • Before the discussion episode in the first lesson, ZH presented the mathematics task with the help of dynamic geometry software. • There is no interaction between ZH and his students • Only when ZH needed to present or explain the requirements of the tasks, he chose to control the explaining process. • After that, ZH changing his organization into letting students make explanation by posing several questions. He chose some of the students to answer these questions in order to let others know what happened on the screen and the geometry features. • ZH put the diagram designed based on the task situation on the screen with the help of dynamic geometry. • One student was asked to explain what happened on the screen, during that time, we could find point P began to move from point A to B then, from B to C. 15

Example episodes Spot-and-show • ZH put students’ work on the screen and let her explain her solving strategy • ZH gave the students some feedbacks or posed some questions to let them make deep thinking. • The topics came from the students’ work based on the task situation. • In this lesson, ZH did not chose the students’ work before the class, he chose them when students solved the problems and at the same time he put them on the screen and made them as a topic of following discussion. 16

Conclusion • The model of teaching process of this Chinese teacher • • • The following model could be used to present the process of ZH’s didactical practice: explain-the-screen (teacher, if needed) -----whole-class-discussion ----- spot-and-show (if possible) ------ guide-and-explain (one or more students) ----- explain-the-screen (teacher). Main features of the instrumental orchestration in Chinese mathematics classes • Teacher makes more control in teaching process • Students have less time to interact with technology • ZH also tried to organized the teaching process in order to let students have a chance to participate Tendency of Chinese mathematics education • ZH began to notice students could explain mathematics contents by themselves • Letting students have more time to participate mathematics learning process is one of the important tendency of Chinese mathematics education. 17

Questions What is the relation between teacher’s document work and teacher’s knowledge? 18

Examples of students’ operate dynamic geometry from other lessons • Example 1

Examples of students’ operate dynamic geometry from other lessons • Example 2

Examples of students’ operate dynamic geometry from other lessons • Example 3

Reference Assude, T. (2007). Teachers’ practices and degree of ICT integration. In Proceedings of the fifth congress of the European Society for Research in Mathematics Education (pp. 1339 -1348). Assude, T. , & Gelis, J. -M. (2002). La dialectique ancien-nouveau dans l’intégration de Cabri-géomètre à l’école primaire. Educational Studies in Mathematics, 50(3), 259– 287. Cayton, C. , Hollebrands, K. , Okumuş, S. , & Boehm, E. (2017). Pivotal teaching moments in technology-intensive secondary geometry classrooms. Journal of Mathematics Teacher Education, 20(1), 75– 100. https: //doi. org/10. 1007/s 10857 -015 -9314 -y Clark-Wilson, A. (2013). The mathematics teacher in the digital era: an international perspective on technology focused professional development. New York: Springer. Drijvers, P. , Doorman, M. , Boon, P. , Reed, H. , & Gravemeijer, K. (2010). The teacher and the tool: instrumental orchestrations in the technology-rich mathematics classroom. Educational Studies in Mathematics, 75(2), 213– 234. https: //doi. org/10. 1007/s 10649 -010 -9254 -5 Drijvers, P. , Tacoma, S. , Besamusca, A. , Doorman, M. , & Boon, P. (2013). Digital resources inviting changes in mid-adopting teachers’ practices and orchestrations. ZDM, 45(7), 987– 1001. https: //doi. org/10. 1007/s 11858 -013 -0535 -1 Hegedus, S. , Laborde, C. , Brady, C. , Dalton, S. , Siller, H. -S. , Tabach, M. , … Moreno-Armella, L. (2017). Uses of Technology in Upper Secondary Mathematics Education. In S. Hegedus, C. Laborde, C. Brady, S. Dalton, H. -S. Siller, M. Tabach, … L. Moreno-Armella, Uses of Technology in Upper Secondary Mathematics Education (pp. 1– 36). Cham: Springer International Publishing. https: //doi. org/10. 1007/978 -3 -319 -42611 -2_1 Jenson, J. , & Rose, C. B. (2006). Finding space for technology: Pedagogical observations on the organization of computers in school environments. Canadian Journal of Learning and Technology / La Revue Canadienne de l’apprentissage et de La Technologie, 32(1). https: //doi. org/10. 21432/T 2 NS 3 Z Lagrange, J. -B. , Artigue, M. , Laborde, C. , & Trouche, L. (2003). Technology and Mathematics Education: A Multidimensional Study of the Evolution of Research and Innovation. In A. J. Bishop, M. A. Clements, C. Keitel, J. Kilpatrick, & F. K. S. Leung (Eds. ), Second International Handbook of Mathematics Education (pp. 237– 269). Dordrecht: Springer Netherlands. https: //doi. org/10. 1007/978 -94 -010 -0273 -8_9 Sinclair, N. , Bartolini Bussi, M. G. , de Villiers, M. , Jones, K. , Kortenkamp, U. , Leung, A. , & Owens, K. (2016). Recent research on geometry education: an ICME-13 survey team report. ZDM, 48(5), 691– 719. https: //doi. org/10. 1007/s 11858 -016 -0796 -6 Trgalova, J. , Jahn, A. P. , & Soury-Lavergne, S. (2009). Quality process for dynamic geometry resources: the Intergeo project. In Proceedings of CERME (Vol. 6). Retrieved from http: //ife. ens-lyon. fr/publications/edition-electronique/cerme 6/wg 7 -12 -trgalovajahnssl. pdf 22 Trouche, L. (2004). Managing the complexity of human/machine interactions in computerized learning environments: Guiding students’ command process through instrumental orchestrations. International Journal of Computers for Mathematical Learning, 9(3), 281– 307.

Thank you for listening

Workshop Task Description The first task contained one moving point P. At first, point P is coincide with point A then it moves from A to B to C to D. Students need to find out the mathematical relation between the area of triangle APD and the length of moving trace. The second task contained two moving points, point A and C, but these points do not move according to line but like a circle. There is a right triangle ABC, ∠C=90°, BC=4, AC=3. ZH makes triangle ABC turns around point B to make point A on the line BC (point A’), students need to find the length of segment AA’ The third task, ZH designed one rectangle ABCD. There is a point E which moves along segment BC, from point B to C. Point B’ is a symmetry point of point B according to segment AE like the figure shown. Students need to find what kind of trace point B’ moves when point E is moving along BC If you will use these tasks in mathematics lessons, how do you modify them to meet your own teaching objectives?