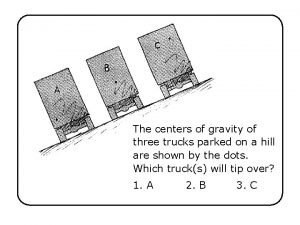
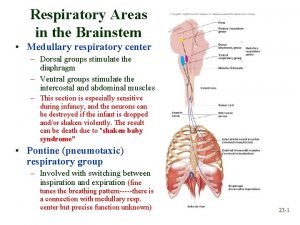
Instant Centers of Velocities Introduction Instant Centers of

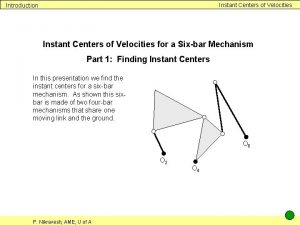
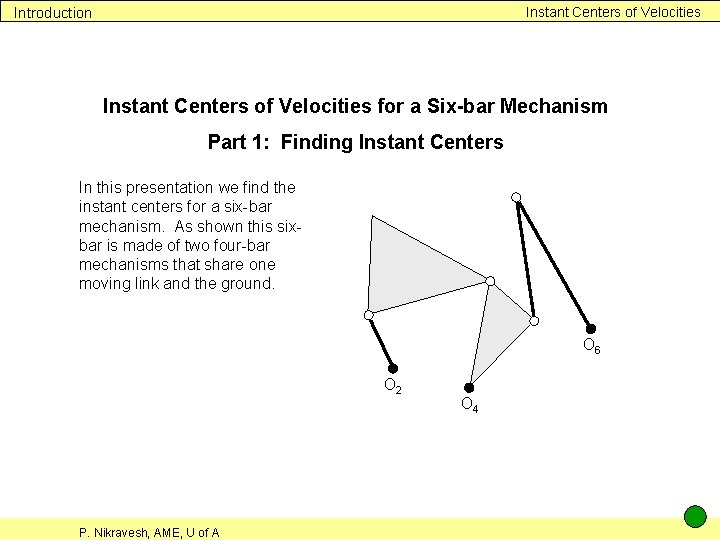
Instant Centers of Velocities Introduction Instant Centers of Velocities for a Six-bar Mechanism Part 1: Finding Instant Centers In this presentation we find the instant centers for a six-bar mechanism. As shown this sixbar is made of two four-bar mechanisms that share one moving link and the ground. O 6 O 2 P. Nikravesh, AME, U of A O 4

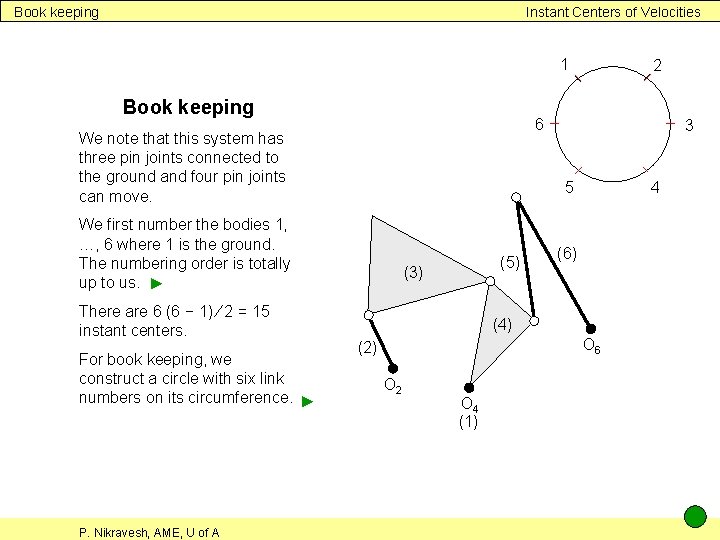
Book keeping Instant Centers of Velocities 1 Book keeping 6 We note that this system has three pin joints connected to the ground and four pin joints can move. For book keeping, we construct a circle with six link numbers on its circumference. ► P. Nikravesh, AME, U of A 3 5 We first number the bodies 1, …, 6 where 1 is the ground. The numbering order is totally up to us. ► There are 6 (6 − 1) ∕ 2 = 15 instant centers. 2 (5) (3) 4 (6) (4) O 6 (2) O 2 O 4 (1)

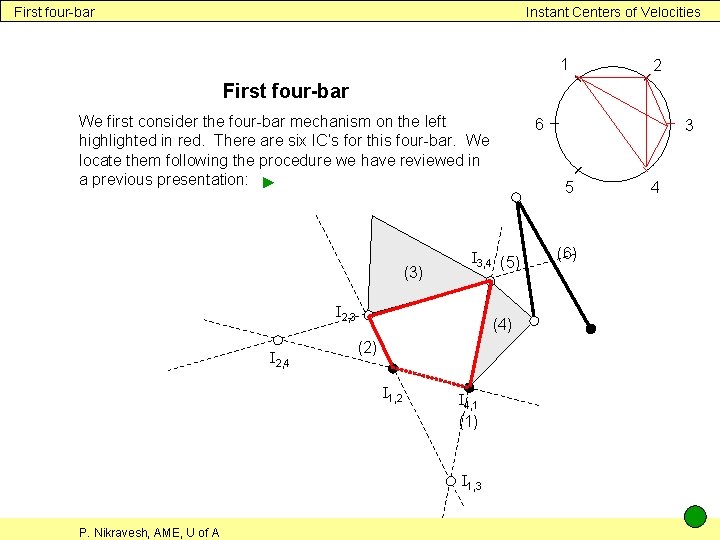
First four-bar Instant Centers of Velocities 1 2 First four-bar We first consider the four-bar mechanism on the left highlighted in red. There are six IC’s for this four-bar. We locate them following the procedure we have reviewed in a previous presentation: ► (3) (4) (2) I 1, 2 I 4, 1 (1) I 1, 3 P. Nikravesh, AME, U of A 3 5 I 3, 4 (5) I 2, 3 I 2, 4 6 (6) 4

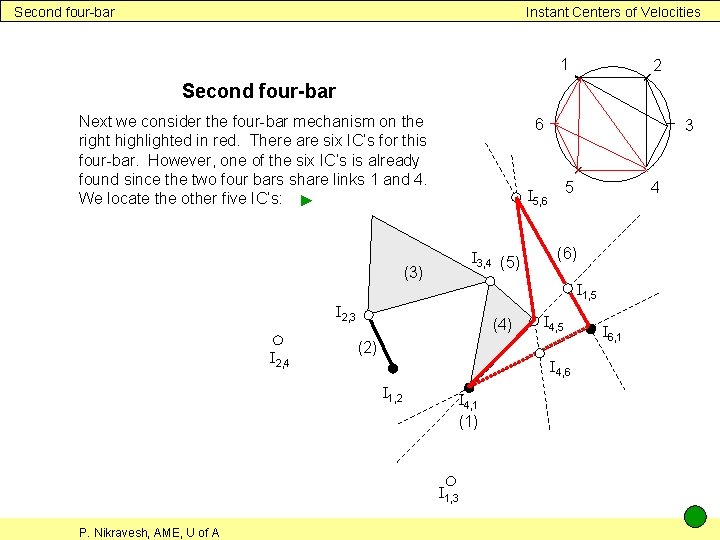
Second four-bar Instant Centers of Velocities 1 2 Second four-bar Next we consider the four-bar mechanism on the right highlighted in red. There are six IC’s for this four-bar. However, one of the six IC’s is already found since the two four bars share links 1 and 4. We locate the other five IC’s: ► 6 I 3, 4 (5) (4) (6) I 4, 5 (2) I 4, 6 I 1, 2 4 I 1, 5 I 2, 3 I 4, 1 (1) I 1, 3 P. Nikravesh, AME, U of A 5 I 5, 6 (3) I 2, 4 3 I 6, 1

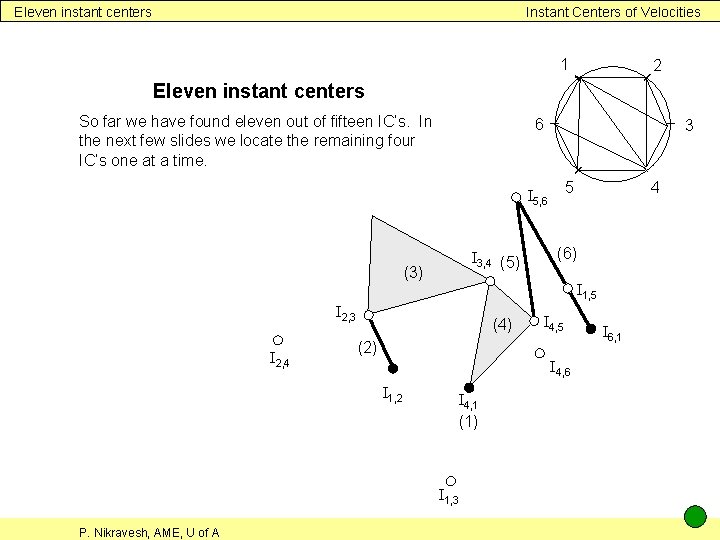
Eleven instant centers Instant Centers of Velocities 1 2 Eleven instant centers So far we have found eleven out of fifteen IC’s. In the next few slides we locate the remaining four IC’s one at a time. 6 3 5 I 5, 6 I 3, 4 (5) (3) (4) I 4, 5 (2) I 4, 6 I 1, 2 I 4, 1 (1) I 1, 3 P. Nikravesh, AME, U of A (6) I 1, 5 I 2, 3 I 2, 4 4 I 6, 1

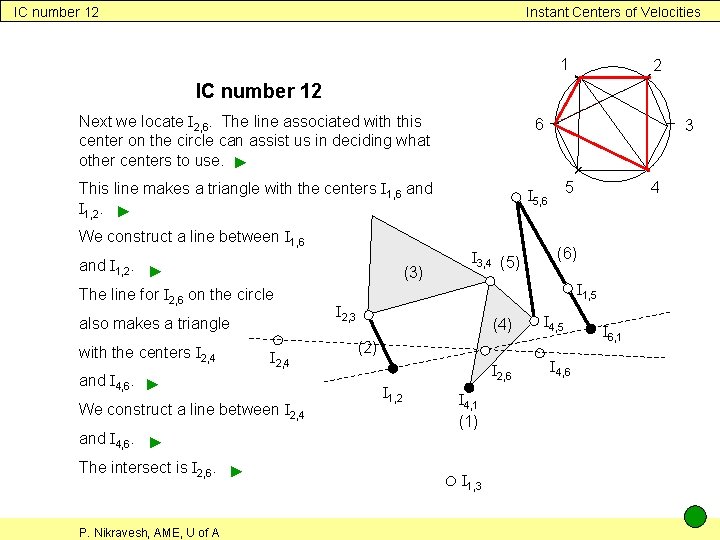
IC number 12 Instant Centers of Velocities 1 2 IC number 12 Next we locate I 2, 6. The line associated with this center on the circle can assist us in deciding what other centers to use. ► 6 This line makes a triangle with the centers I 1, 6 and I 1, 2. ► I 5, 6 We construct a line between I 1, 6 and I 1, 2. ► The line for I 2, 6 on the circle also makes a triangle with the centers I 2, 4 and I 4, 6. ► We construct a line between I 2, 4 and I 4, 6. ► The intersect is I 2, 6. ► P. Nikravesh, AME, U of A (3) I 3, 4 (5) 3 5 (6) I 1, 5 I 2, 3 (4) I 4, 5 (2) I 2, 6 I 1, 2 4 I 4, 1 (1) I 1, 3 I 4, 6 I 6, 1

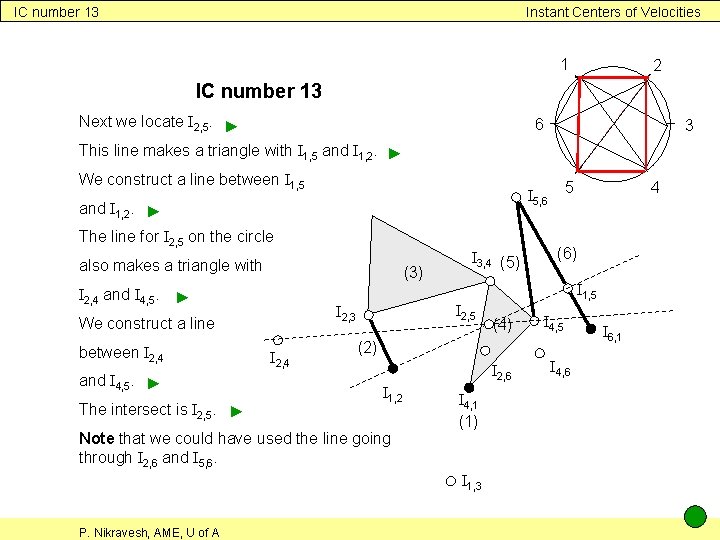
IC number 13 Instant Centers of Velocities 1 2 IC number 13 Next we locate I 2, 5. ► This line makes a triangle with I 1, 5 and I 1, 2. ► 6 We construct a line between I 1, 5 The line for I 2, 5 on the circle also makes a triangle with (3) between I 2, 4 and I 4, 5. ► The intersect is I 2, 5. ► I 2, 4 I 3, 4 (5) (4) I 2, 6 Note that we could have used the line going through I 2, 6 and I 5, 6. I 4, 1 (1) I 1, 3 P. Nikravesh, AME, U of A (6) I 4, 5 (2) I 1, 2 4 I 1, 5 I 2, 3 We construct a line 5 I 5, 6 and I 1, 2. ► I 2, 4 and I 4, 5. ► 3 I 4, 6 I 6, 1

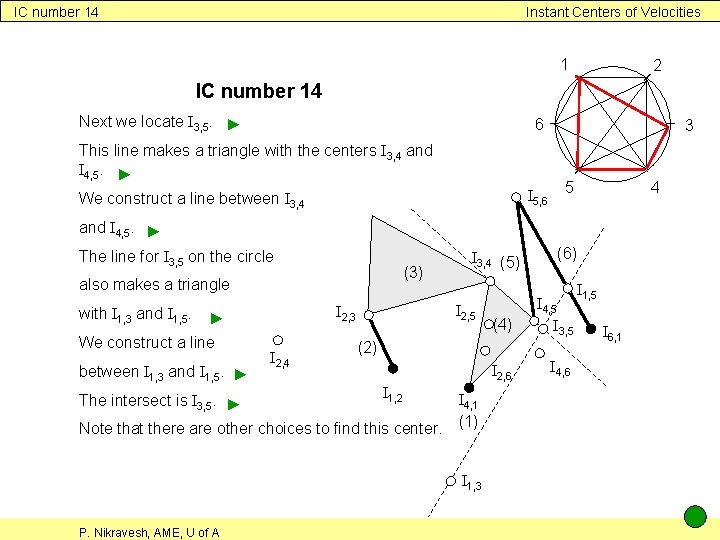
IC number 14 Instant Centers of Velocities 1 2 IC number 14 Next we locate I 3, 5. ► 6 This line makes a triangle with the centers I 3, 4 and I 4, 5. ► I 5, 6 We construct a line between I 3, 4 3 5 4 and I 4, 5. ► The line for I 3, 5 on the circle (3) also makes a triangle with I 1, 3 and I 1, 5. We construct a line between I 1, 3 and I 1, 5. ► The intersect is I 3, 5. ► I 2, 5 I 2, 3 ► I 2, 4 I 3, 4 (5) (4) I 4, 5 I 3, 5 I 2, 6 I 4, 6 (2) I 1, 2 Note that there are other choices to find this center. I 4, 1 (1) I 1, 3 P. Nikravesh, AME, U of A (6) I 1, 5 I 6, 1

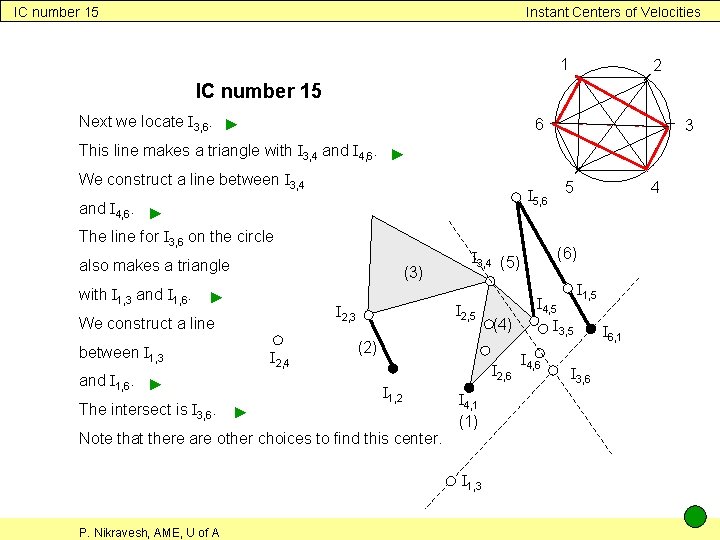
IC number 15 Instant Centers of Velocities 1 2 IC number 15 Next we locate I 3, 6. ► 6 3 This line makes a triangle with I 3, 4 and I 4, 6. ► We construct a line between I 3, 4 I 5, 6 and I 4, 6. ► The line for I 3, 6 on the circle also makes a triangle with I 1, 3 and I 1, 6. (3) ► We construct a line between I 1, 3 I 2, 4 and I 1, 6. ► The intersect is I 3, 6. ► (2) I 2, 6 I 1, 2 Note that there are other choices to find this center. I 4, 1 (1) I 1, 3 P. Nikravesh, AME, U of A (4) 4 (6) I 3, 4 (5) I 2, 5 I 2, 3 5 I 4, 5 I 3, 5 I 4, 6 I 1, 5 I 3, 6 I 6, 1

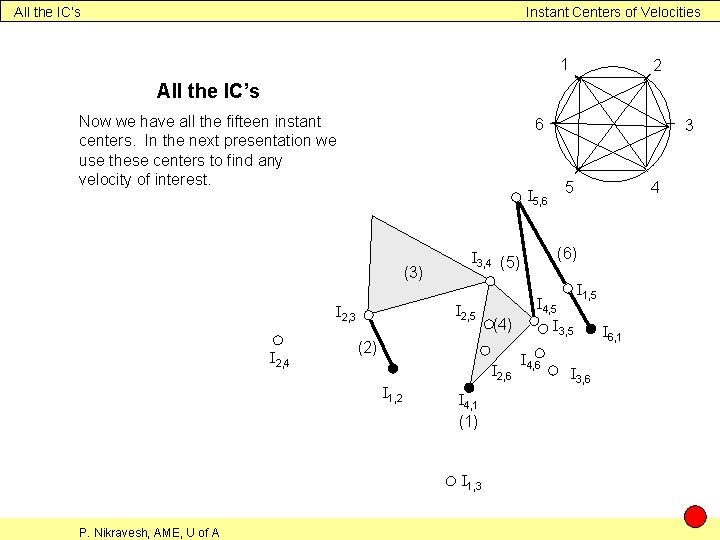
All the IC’s Instant Centers of Velocities 1 2 All the IC’s Now we have all the fifteen instant centers. In the next presentation we use these centers to find any velocity of interest. 6 I 5, 6 (3) I 2, 4 (2) I 2, 6 I 1, 2 I 4, 1 (1) I 1, 3 P. Nikravesh, AME, U of A (4) 5 4 (6) I 3, 4 (5) I 2, 5 I 2, 3 3 I 4, 5 I 3, 5 I 4, 6 I 1, 5 I 3, 6 I 6, 1