Instant Centers for a Fourbar Introduction Velocity Analysis

Instant Centers for a Four-bar Introduction Velocity Analysis with Instant Centers for a Four-bar Mechanism This presentation shows how to perform velocity analysis for a four-bar mechanism with the method of instant centers. It is assumed that the dimensions for the links are known and the analysis is being performed at a given (known) configuration. Since the four-bar has one degree-of-freedom, the angular velocity of one of the links (or one other velocity information) must be given as well. For a given four-bar mechanism the velocity analysis consists of two steps: 1. Finding the instant centers 2. Finding velocities 3. Note that the instant center method is a graphical method. P. Nikravesh, AME, U of A

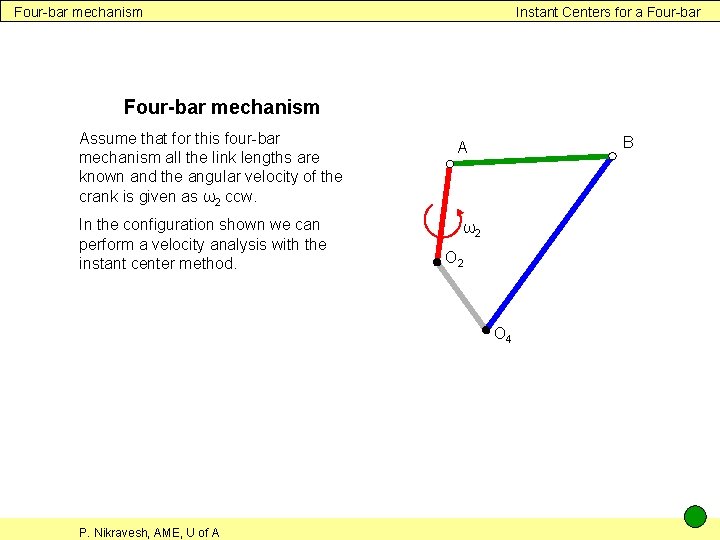
Four-bar mechanism Instant Centers for a Four-bar mechanism Assume that for this four-bar mechanism all the link lengths are known and the angular velocity of the crank is given as ω2 ccw. In the configuration shown we can perform a velocity analysis with the instant center method. B A ω2 O 4 P. Nikravesh, AME, U of A

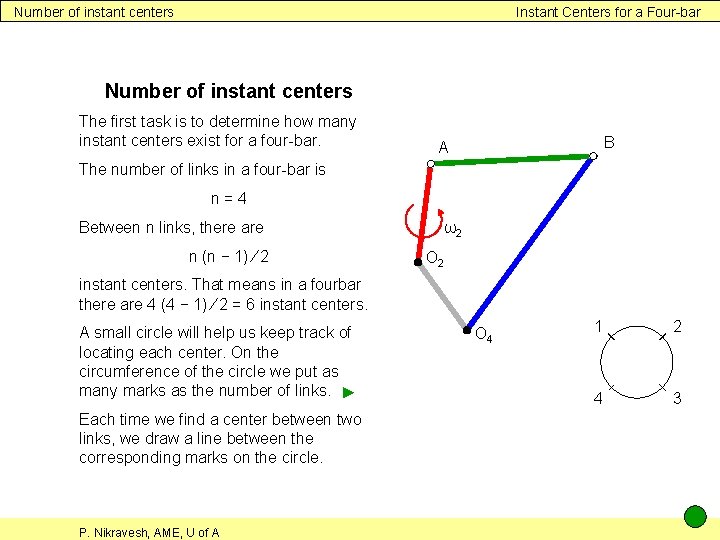
Number of instant centers Instant Centers for a Four-bar Number of instant centers The first task is to determine how many instant centers exist for a four-bar. B A The number of links in a four-bar is n=4 Between n links, there are n (n − 1) ∕ 2 ω2 O 2 instant centers. That means in a fourbar there are 4 (4 − 1) ∕ 2 = 6 instant centers. A small circle will help us keep track of locating each center. On the circumference of the circle we put as many marks as the number of links. ► Each time we find a center between two links, we draw a line between the corresponding marks on the circle. P. Nikravesh, AME, U of A O 4 1 2 4 3

Finding the instant centers Instant Centers for a Four-bar Finding the instant centers Four of the centers are already known: They are the four pin joints. I 2, 4 ► We don’t know I but we know B = I 3, 4 A = I 2, 3 1, 3 that it lies on the same line as I 4, 1 and I 3, 4. I 1, 3 also lies ► on the same line as I 2, 1 and I 3, 2. The point of intersection is I 1, 3. ► I is also unknown but it lies on► ω2 O 2 = I 1, 2 2, 4 the same line as I 3, 4 and I 2, 3. I 2, 4 also lies on the same line as ► I 4, 1 and I 1, 2. The point of intersection is I 2, 4. ► Now we have found all 6 centers► O 4 = I 4, 1 I 1, 3 P. Nikravesh, AME, U of A 1 2 4 3

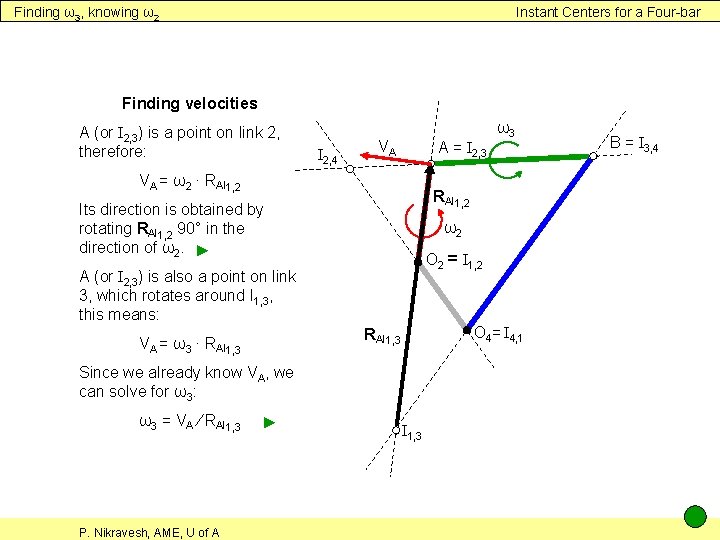
Finding ω3, knowing ω2 Instant Centers for a Four-bar Finding velocities A (or I 2, 3) is a point on link 2, therefore: I 2, 4 VA A = I 2, 3 VA = ω2 ∙ RAI 1, 2 Its direction is obtained by rotating RAI 1, 2 90° in the direction of ω2. ► ω2 O 2 = I 1, 2 A (or I 2, 3) is also a point on link 3, which rotates around I 1, 3, this means: O 4= I 4, 1 RAI 1, 3 VA = ω3 ∙ RAI 1, 3 Since we already know VA, we can solve for ω3: ω3 = VA ∕ RAI 1, 3 P. Nikravesh, AME, U of A ► ω3 I 1, 3 B = I 3, 4

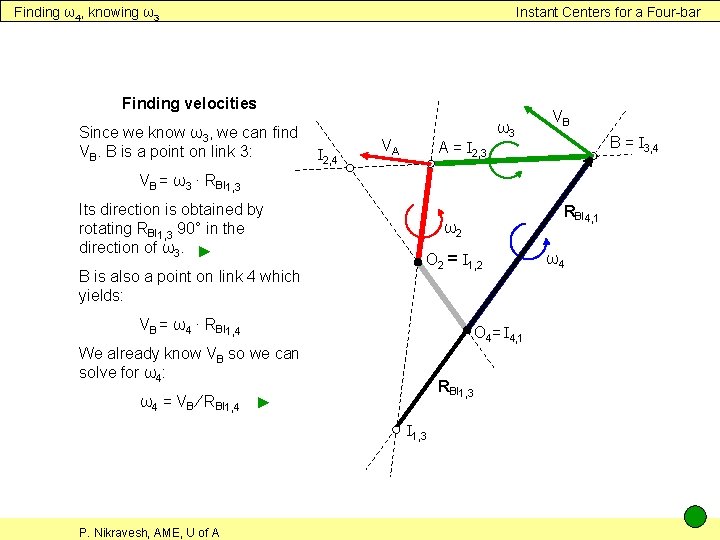
Finding ω4, knowing ω3 Instant Centers for a Four-bar Finding velocities Since we know ω3, we can find VB. B is a point on link 3: I 2, 4 VA A = I 2, 3 ω3 VB B = I 3, 4 VB = ω3 ∙ RBI 1, 3 Its direction is obtained by rotating RBI 1, 3 90° in the direction of ω3. ► B is also a point on link 4 which yields: ω2 O 2 = I 1, 2 VB = ω4 ∙ RBI 1, 4 O 4= I 4, 1 We already know VB so we can solve for ω4: RBI 1, 3 ω4 = VB ∕ RBI 1, 4 ► I 1, 3 P. Nikravesh, AME, U of A RBI 4, 1 ω4

Finding ω4, knowing ω2 Instant Centers for a Four-bar Another approach We could have determined ω4 without knowing ω3: I 2, 4 is a point on link 2, therefore: VI 2, 4 = ω2 ∙ RI 2, 4 I 1, 2 Its direction is obtained by rotating RI 2, 4 I 1, 2 90° in the direction of ω2. ► ω2 O 2 = I 1, 2 I 2, 4 is also a point on link 4, which rotates around I 4, 1. This means: RI 2, 4 I 4, 1 O 4= I 4, 1 VI 2, 4 = ω4 ∙ RI 2, 4 I 4, 1 We already know VI 2, 4 so we can solve for ω4: ω4 = VI 2, 4 ∕ RI 2, 4 I 4, 1 P. Nikravesh, AME, U of A B = I 3, 4 A = I 2, 3 I 2, 4 I 1, 3 ► ω4

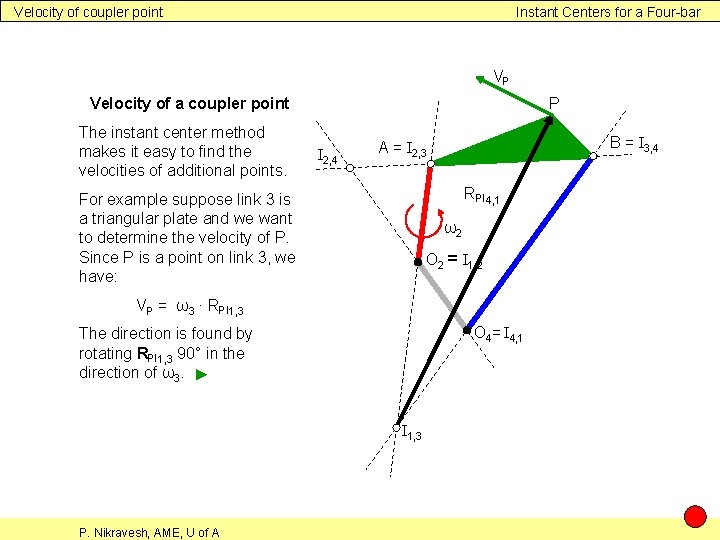
Velocity of coupler point Instant Centers for a Four-bar VP P Velocity of a coupler point The instant center method makes it easy to find the velocities of additional points. I 2, 4 B = I 3, 4 A = I 2, 3 RPI 4, 1 For example suppose link 3 is a triangular plate and we want to determine the velocity of P. Since P is a point on link 3, we have: ω2 O 2 = I 1, 2 VP = ω3 ∙ RPI 1, 3 O 4= I 4, 1 The direction is found by rotating RPI 1, 3 90° in the direction of ω3. ► I 1, 3 P. Nikravesh, AME, U of A